
Figure 1: EG and CG for If a farmer owns a donkey, then he beats it.
John F. Sowa
VivoMind LLC
Abstract. Conceptual graphs (CGs) are a version of logic designed to represent the semantics of natural language (NL). CG logic is based on Peirce's existential graphs, and CG notation is based on the formalisms of theoretical and computational linguistics. CGs can represent the modal, metalevel, and higher-order expressions of natural languages, but subsets of CG logic have also been used to represent description logics, expert-system rules, and frame-like knowledge bases. For ontology, CGs can represent the concept types and predicates defined in other versions of logic, but the simplest CG features have direct counterparts in NL words, phrases, and lexical structures. Consequently, conceptual graphs are commonly used as an intermediate language between NL and computer-oriented notations. This article emphasizes the CG features that support the ontology implicit in natural languages.
Since the time of Aristotle, the traditional purpose of logic has been to represent the semantics of natural language in a form that clarifies and facilitates the operations of reasoning. During the 20th century, however, logicians developed logic as a tool for analyzing the foundations of mathematics, while largely ignoring its applications to language. Not until the late 1960s did computational linguists such as Woods (1968) and logicians such as Montague (1970) begin to address the problems of translating language to logic. Unfortunately, many logicians ignored those features of language that do not have a simple mapping to their favorite notation for logic. Montague stated his bias explicitly:
There is in my opinion no important theoretical difference between natural languages and the artificial languages of logicians; indeed, I consider it possible to comprehend the syntax and semantics of both kinds of languages within a single natural and mathematically precise theory.... The basic aim of semantics is to characterize the notions of a true sentence (under a given interpretation) and of entailment, while that of syntax is to characterize the various syntactical categories, especially the set of declarative sentences.Montague's thesis polarized linguists into two camps: those who believe that the ideal notation for semantics is some version of logic, and those who maintain that logic has little or no relationship to the fundamental structure of natural language. Linguists in one camp rarely, if ever, read the publications of those in the other.
Conceptual graphs were designed to bridge the gap between the two camps. Like other versions of logic, they have a model-theoretic semantics. But unlike predicate calculus, their syntax is designed to emphasize the features of natural language. Their logical structure is based on the existential graphs of Peirce (1909), who also invented the algebraic notation for predicate calculus (1880, 1885). For EGs, Peirce used only three operators to express full first-order logic (FOL): an existential quantifier expressed by a bar or linked structure of bars called a line of identity; negation expressed by an oval context delimiter; and conjunction expressed by the occurrence of two or more graphs in the same context. To illustrate the EG and CG notations, Figure 1 shows both kinds of graphs for the sentence If a farmer owns a donkey, then he beats it.

Figure 1: EG and CG for If a farmer owns a donkey, then he beats it.
When the EG in Figure 1 is translated to predicate calculus, each of the two ovals maps to the symbol ~ for negation. The two lines of identity map to two quantified variables: (∃x) represents the bars that link farmer to the left side of owns and beats; (∃y) represents the bars that link donkey to the right side of the same two verbs. The words farmer and donkey map to monadic predicates; owns and beats map to dyadic predicates. With the ∧ symbol for conjunction, the result is
~(∃x)(∃y)(farmer(x) ∧ donkey(y) ∧ owns(x,y) ∧ ~beats(x,y)).
A nest of two ovals, as in Figure 1, is what Peirce called a scroll. It represents implication, since ~(p∧~q) is equivalent to p⊃q. Using the ⊃ symbol, the formula may be rewritten
(∀x)(∀y)((farmer(x) ∧ donkey(y) ∧ owns(x,y)) ⊃ beats(x,y)).The CG in Figure 1 may be considered a typed version of the EG. The boxes [Farmer] and [Donkey] represent typed quantifiers (∃x:Farmer) and (∃y:Donkey). The ovals (Owns) and (Beats) represent relations, whose attached arcs link to the boxes that represent the arguments. The large boxes with the symbol ¬ in front correspond to Peirce's ovals that represent negation. As a result, the CG corresponds to the following formula:
(∀x:Farmer)(∀y:Donkey)(owns(x,y) ⊃ beats(x,y)).These formulas illustrate a peculiar feature of predicate calculus: in order to keep the variables x and y within the scope of the quantifiers, the existential quantifiers for the phrases a farmer and a donkey must be moved to the front of the formula and be translated to universal quantifiers. This puzzling feature of logic has been a matter of debate among linguists and logicians since the middle ages.
Hans Kamp, a student of Montague's, once spent a summer translating English sentences from a scientific article to predicate calculus. During the course of his work, he was troubled by the same irregularities that puzzled the medieval logicians. To simplify the mapping from language to logic, Kamp developed discourse representation structures (DRSs) with an explicit notation for contexts. In terms of those structures, Kamp defined the rules of discourse representation theory for mapping quantifiers, determiners, and pronouns from language to logic (Kamp & Reyle 1993).
Although Kamp had not been aware of Peirce's existential graphs, his DRSs are isomorphic to EGs. The diagram on the right of Figure 2 is a DRS for the donkey sentence, If there exist a farmer x and a donkey y and x owns y, then x beats y. The two boxes connected by an arrow represent an implication where the antecedent includes the consequent within its scope.

Figure 2: EG and DRS for If a farmer owns a donkey, then he beats it.
The EG and DRS notations look quite different, but they have the same primitives, the same scoping rules for quantifiers, and the same translation to predicate calculus. Most importantly, they represent implication in a form that does not require existential quantifiers to be translated to universals. Peirce's motivation for the EG notation was to simplify the logical structures and rules of inference. Kamp's motivation was to simplify the mapping from language to logic. Remarkably, they converged on isomorphic structures. Therefore, Peirce's inference rules and Kamp's discourse rules apply equally well to the EG, CG, and DRS notations.
The ontology of Figures 1 and 2 treats the verbs owns and beats as dyadic relations between the farmer and the donkey. That ontology, which is often used in elementary logic books, fails to capture the nuances of natural language. Peirce maintained that events and properties are just as significant as physical objects. When he translated English sentences to logic, he often assigned quantified variables to verbs and adjectives as well as nouns. In his ontology, Whitehead (1929) maintained that the ultimate reality is process-like and that so-called concrete objects are relatively slow processes that manifest themselves as "recurring event types" characterized by "forms of definiteness". The need to treat events and properties as entities with the same status as physical objects was independently rediscovered in the 1960s by philosophers, linguists, and computer scientists.
Figure 3 revises the ontology of Figure 1 to represent the verbs by concepts that have the same status as the concepts for the farmer and the donkey. It also uses the type labels If and Then instead of the negation signs; each of those labels is defined as the negation of a proposition, and the double nest represents an implication equivalent to Figure 1.

Figure 3: Extended CG for If a farmer owns a donkey, then he beats it.
Four additional relations are used in Figure 3 to link the concepts [Own] and [Beat] to [Farmer] and [Donkey]. The kinds of relations linked to the two verbs, however, are very different. Ownership is a state experienced by the farmer, which has no physical effect on the donkey, but beating is an action that has a direct, painful effect. The labels for the four relations are taken from the names of the thematic roles or case relations used in linguistics: experiencer (Expr) links the concept [Own] to the concept [Farmer]; theme (Thme) links [Own] to [Donkey]; agent (Agnt) links [Beat] to [Farmer]; and patient (Ptnt) links [Beat] to [Donkey]. Those relations map to dyadic predicates with the arrow pointing toward the circle as the first argument and the arrow pointing away from the circle as the second argument. Following is the formula:
(∀x:Farmer)(∀y:Donkey)(∀z:Own)(∃w:Beat)This formula may be read For every farmer x, donkey y, and owning z, there exists a beating w such that if the experiencer of z is x and the theme of z is y, then the agent of w is x and the patient of w is y. The equivalent CG in Figure 3 may be read If a farmer is the experiencer of owning of which the donkey is the theme, then the farmer is the agent of beating of which the donkey is the patient. The relations that express thematic roles are important for NL semantics, but they are not usually expressed in ordinary English. When they are left implicit, Figure 3 may be read as the simpler sentence If a farmer owns a donkey, then the farmer beats the donkey.
((Expr(z,x) ∧ (Thme(z,y)) ⊃ (Agnt(w,x) ∧ (Ptnt(w,y)))
The design goal for conceptual graphs is a balance between the simplicity of Peirce's existential graphs and the flexibility, adaptability, and expressive power of natural languages. With the minimalism of EGs, Peirce demonstrated that complex ideas can be expressed with repeated application of a small number of primitives. But many features of language, such as plurals, indexicals, and generalized quantifiers, can be expressed more succinctly with a richer notation. To maintain a balance, the CG notation is based on three design principles:
In logic, the implication operator determines a generalization hierarchy: if a graph or formula p implies another graph or formula q, then p is more specialized and q is more general. (It's also possible that p and q are logically equivalent.) When Peirce introduced the implication operator into Boolean algebra, he used a symbol for less-than-or-equal, since the truth value of the antecedent is always less than or equal to the truth value of the consequent. Therefore, the symbol ≤ may be used to represent generalization: p≤q means that p is less general or equivalent to q.
Figure 4 shows a generalization hierarchy in which the most general CG is at the top. Each dark line in Figure 4 represents the ≤ operator: the CG above is a generalization, and the CG below is a specialization. The top CG says that an animate being is the agent of some act that has an entity as the theme of the act. Below it are two specializations: a CG for a robot washing a truck, and a CG for an animal chasing an entity. The CG for an animal chasing an entity has three specializations: a human chasing a human, a cat chasing a mouse, and the dog Macula chasing a Chevrolet.

Figure 4: A generalization hierarchy of CGs
All operations on conceptual graphs are based on combinations of six canonical formation rules, each of which performs one basic graph operation. Logically, each rule has one of three possible effects on a CG: the rule can make it more specialized, more generalized, or logically equivalent but with a modified shape. Each rule has an inverse rule that restores a CG to its original form. The inverse of specialization is generalization, the inverse of generalization is specialization, and the inverse of equivalence is another equivalence.
All the graphs in Figure 4 belong to the existential-conjunctive subset of logic, whose only operators are the existential quantifier ∃ and the conjunction ∧. For this subset, the canonical formation rules take the forms illustrated in Figures 5, 6, and 7. These rules are fundamentally graphical: they are easier to show than to describe. For the formal definitions, see the draft CG standard (Sowa 2003).

Figure 5: Copy and simplify rules
Figure 5 shows the first two rules: copy and simplify. At the top is a CG for the sentence "The cat Yojo is chasing a mouse." The down arrow represents two applications of the copy rule. The first copies the Agnt relation, and the second copies the subgraph →(Thme)→[Mouse]. The two copies of the concept [Mouse] at the bottom of Figure 5 are connected by a dotted line called a coreference link; that link, which corresponds to an equal sign = in predicate calculus, indicates that both concepts must refer to the same individual. Since the new copies do not add any information, they may be erased without losing information. The up arrow represents the simplify rule, which performs the inverse operation of erasing redundant copies. The copy and simplify rules are called equivalence rules because any two CGs that can be transformed from one to the other by any combination of copy and simplify rules are logically equivalent. The two formulas in predicate calculus that are derived from Figure 5 are also logically equivalent. The top CG maps to the following formula:
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z)),In the formula that corresponds to the bottom CG, the equality z=w represents the coreference link that connects the two copies of [Mouse]:
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(∃w:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ agnt(y,x) ∧ thme(y,z) ∧ thme(y,w) ∧ z=w).By the inference rules of predicate calculus, either of these two formulas can be derived from the other.
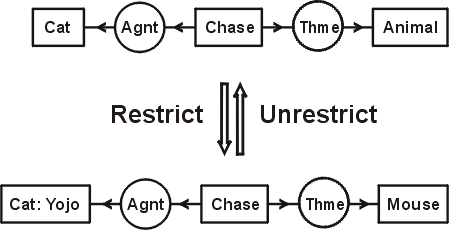
Figure 6: Restrict and unrestrict rules
Figure 6 illustrates the restrict and unrestrict rules. At the top is a CG for the sentence "A cat is chasing an animal." Two applications of the restrict rule transform it to the CG for "The cat Yojo is chasing a mouse." The first step is a restriction by referent of the concept [Cat], which represents some indefinite cat, to the more specific concept [Cat: Yojo], which represents a particular cat named Yojo. The second step is a restriction by type of the concept [Animal] to a concept of the subtype [Mouse]. Two applications of the unrestrict rule perform the inverse transformation of the bottom graph to the top graph. The restrict rule is a specialization rule, and the unrestrict rule is a generalization rule. The more specialized graph implies the more general one: if the cat Yojo is chasing a mouse, it follows that a cat is chasing an animal. The same implication holds for the corresponding formulas in predicate calculus. The more general formula
(∃x:Cat)(∃y:Chase)(∃z:Animal)(agnt(y,x) ∧ thme(y,z))
is implied by the more specialized formula
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z)).

Figure 7: Join and detach rules
Figure 7 illustrates the join and detach rules. At the top are two CGs for the sentences "Yojo is chasing a mouse" and "A mouse is brown." The join rule overlays the two identical copies of the concept [Mouse], to form a single CG for the sentence "Yojo is chasing a brown mouse." The detach rule performs the inverse operation. The result of join is a more specialized graph that implies the one derived by detach. The same implication holds for the corresponding formulas in predicate calculus. The conjunction of the formulas for the top two CGs
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z))is implied by the formula for the bottom CG(∃w:Mouse)(∃v:Brown)attr(w,v)
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(∃v:Brown)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z) ∧ attr(z,v)).
These rules can be generalized to full first-order logic by specifying how they interact with negation. In CGs, each negation is represented by a context that has an attached relation of type Neg or its abbreviation by the symbol ¬ or ~. Negations may also be included in the definition of some type label, such as If and Then, which are defined as the type Proposition with an attached Neg relation. A positive context is nested in an even number of negations (possibly zero). A negative context is nested in an odd number of negations. The following four principles determine how negations affect the rules:
By handling the syntactic details of conceptual graphs, the generalization and specialization rules enable the rules of inference to be stated in a form that is independent of the graph notation. For each of the six canonical formation rules for CGs, there is an equivalent rule for predicate calculus or any other notation for classical FOL. To derive those rules from the CG rules, start by showing the effect of each rule on the existential-conjunctive subset (no operators other than ∃ and ∧). To handle negation, add one to the negation count for each subgraph or subformula that is governed by a ~ symbol. For other operators (∀, ⊃, and ∨), count the number of negations in their definitions. For example, p⊃q is defined as ~(p∧~q); therefore, the subformula p is nested inside one additional negation, and the subformula q is nested inside two additional negations.
When the CG rules are applied to other notations, some extensions may be necessary. For example, the blank or empty graph is a well-formed EG or CG, which is always true. In predicate calculus, the blank may be represented by a constant formula T, which is defined to be true. The operation of erasing a graph would correspond to replacing a formula by T. When formulas are erased or inserted, an accompanying conjunction symbol must also be erased or inserted in some notations. Other notations, such as the Knowledge Interchange Format (KIF), are closer to CGs because they only require one conjunction symbol for an arbitrarily long list of conjuncts. In KIF, the formula (and), which is an empty list of conjuncts, may be used as a synonym for the blank graph or T. The DRS notation is even closer to EGs and CGs because it does not use any symbol for conjunction; therefore, the blank may be considered a DRS that is always true.
Peirce's rules, which he stated in terms of existential graphs, form a sound and complete system of inference for first-order logic with equality. If the word graph is considered a synonym for formula or statement, the following adaptation of Peirce's rules can be applied to any notation for FOL, including EGs, CGs, DRS, KIF, or the many variations of predicate calculus. These rules can also be applied to subsets of FOL, such as description logics and Horn-clause rules.
These rules, which Peirce formulated in several equivalent variants from 1897 to 1909, form an elegant and powerful generalization of the rules of natural deduction by Gentzen (1935). Like Gentzen's version, the only axiom is the blank. What makes Peirce's rules more powerful is the option of applying them in any context nested arbitrarily deep. That option shortens many proofs, and it eliminates Gentzen's bookkeeping for making and discharging assumptions. For further discussion and comparison, see MS 514 (Peirce 1909) and the commentary that shows how other rules of inference can be derived from Peirce's rules.
Unlike most proof procedures, which are tightly bound to a particular syntax, this version of Peirce's rules is stated in notation-independent terms of generalization and specialization. In this generalized form, they can even be applied to natural languages. The first step is to show how each syntax rule of the language affects generalization, specialization, and equivalence. In counting the negation depth, it is important to recognize the large number of negation words, such as not, never, none, nothing, nobody, or nowhere. But many other words also contain implicit negations, which affect any context governed by those words. Verbs like prevent or deny, for example, introduce a negation into any clause or phrase in their complement. Many adjectives also have implicit negations: a stuffed bear, for example, lacks essential properties of a bear, such as being alive. After the effects of these features on generalization and specialization have been taken into account, Peirce's rules can be applied to a natural language as easily as to a formal language.
Without any predefined concept or relation types, conceptual graphs are as ontologically neutral as predicate calculus. Natural languages, however, have an enormous amount of built-in ontology, not only in their vocabularies, but also in their syntactic categories, parts of speech, inflections, and so-called function words such as prepositions, conjunctions, and determiners. To satisfy the principle of expressivity, the ontological features that are simply expressed in natural languages should be expressed by CG features that have a correspondingly simple structure.
Since the time of Aristotle, linguists, philosophers, and logicians have implicitly or explicitly observed a version of the expressivity principle in their semantic theories and formalisms. Aristotle derived his ten ontological categories from nominalized forms of verbs, such as essence (ousia) and having (echein), or from common question forms, such as how much or how many, for which Cicero coined the Latin equivalents quantitas and qualitas. The case relations and prepositions that link verbs to nouns were part of the inspiration for Aristotle's four causes or aitia: efficient cause (nominative case); formal cause (accusative case); final cause (dative case); and material cause (instrumental case, which in classical Greek was represented by prepositions with a noun in the dative or genitive case). In deriving their ontologies, other philosophers, such as Kant, Peirce, Husserl, and Whitehead adopted different methodologies, but their categories also reflect features of natural languages. Whatever the methodology, a strong correspondence between NL semantics and ontology is inevitable, since natural languages evolved for the purpose of expressing all concepts that are humanly conceivable.
To represent relations among relations, the CG formalism supports generalization hierarchies (partial orderings) of both concept types and relation types as well as lambda expressions for defining new concept and relation types by parametrizing conceptual graphs. As an example, Figure 8 shows the immediate subtypes of Participant, which is the most general concept type for representing anything that particpates in a process. The type Participant is subdivided by two dichotomies: Determinant or Immanent participants and Source or Product participants. The combination of both dichotomies generates four more subtypes: Initiator, Resource, Goal, and Essence.

Figure 8: Subtypes of Participant
The four types at the bottom of Figure 8 correspond to Aristotle's four aitia, but the terms intiator, resource, goal, and essence better describe the participants of an action than the traditional Latin-based translations of Aristotle's Metaphysics:
Although there are many theories of case relations or thematic roles, most of them group the roles in four categories, which roughly correspond to the traditional nominative, instrumental, dative, and accusative cases. Two classifications that explicitly invoke Aristotle's aitia are the theory of qualia by Pustejovsky (1995), which addresses the ways that nouns are related to other parts of speech, and the classification of thematic roles by Sowa (1996), which analyzes the relations that link verbs to nouns. After analyzing and summarizing various theories, Somers (1987) organized the thematic roles in a matrix with four types of participants at the top and six categories of verbs along the side. In adapting Somers's classification to conceptual graphs, Dick (1991) showed how they could be used to analyze and represent legal arguments. Figure 9 summarizes the Somers-Dick classification in a table with Aristotle's four aitia as the headings.
| Initiator | Resource | Goal | Essence | |
|---|---|---|---|---|
| Action | Agent, Effector | Instrument | Result, Recipient | Patient, Theme |
| Process | Agent, Origin | Matter | Result, Recipient | Patient, Theme |
| Transfer | Agent, Origin | Instrument, Medium | Experiencer, Recipient | Theme |
| Spatial | Origin | Path | Destination | Location |
| Temporal | Start | Duration | Completion | PointInTime |
| Ambient | Origin | Instrument, Matter | Result | Theme |
Figure 9: Thematic roles as subtypes of Aristotle's aitia
In the 24 boxes of the matrix, Somers had some boxes with duplicate role names and some boxes with multiple roles distinguished by properties such as ±animate, ±physical, ±dynamic, or ±volitional. As an example, Van Valin (1993) introduced the role effector for an initiator that causes some event involuntarily, as distinguished from an agent that voluntarily or even deliberately performs it. In surveying various theories of thematic roles, Croft (1998) concluded that the relationships of the participants to the events and to one another would require a detailed representation of the conceptual structures implicit in the definitions of the verbs. In principle, the number of possible relations that could be expressed is open ended, depending on the amount of detail and the complexity of the verb definitions.
In case of ambiguity, the hierarchy shown in Figures 8 and 9 permits a more general type of participant to replace any of its subtypes. In the sentence A dog broke a window, the dog could be an agent that broke it deliberately, an effector that broke it accidentally, or an instrument that was pushed through the window by the actual agent. Each interpretation would be expressed by a different conceptual graph:
[Dog]←(Agnt)←[Break]→(Ptnt)→[Window].
[Dog]←(Efct)←[Break]→(Ptnt)→[Window].
[Dog]←(Inst)←[Break]→(Ptnt)→[Window].
But according to the hierarchy of roles specified by Figures 8 and 9,
Agent, Effector, and Instrument are all
subtypes of Source. Therefore, a single CG with a relation
(Srce) would express the equivalent information:
[Dog]←(Srce)←[Break]→(Ptnt)→[Window].
When further information about the dog's role becomes available,
the relation type Srce can be specialized to one of
the three subtypes Agnt, Efct, or Inst.
As subtypes of Participant, the thematic roles occupy an intermediate level in the ontology. Figure 10 shows a path through the hierarchy from the top levels of the ontology presented by Sowa (2000) to the subtypes of Participant represented in Figure 8. Each of the thematic roles in Figure 9 could then be arranged as a subtype of Initiator, Resource, Goal, or Essence. The incomplete lines in Figure 10 suggest other branches of the KR ontology that have been omitted in order to keep the diagram from being cluttered.

Figure 10: Placement of the thematic roles in the ontology
At the bottom of Figure 10 are more detailed roles based on the analysis by Halliday and Matthiessen (1999): the roles Doer, Senser, and Sayer are subtypes of Agent; and the roles Moved, Said, and Experienced are subtypes of Theme. For more specific purposes, any of those roles could be analyzed further: Doer has a subtype Driver, which has more specific subtypes like BusDriver, TruckDriver, and TaxiDriver.
In principle, the roles could be analyzed as deeply as desired to show distinctions that might be significant in some language, culture, or domain of interest. The method of analyzing roles and relating them to one another is supported by the CG definitional mechanisms. As an example, the following definition says that a taxi driver is an agent who drives a taxi:
TaxiDriver = [Driver: λ]←(Agnt)←[Drive]→(Thme)→[Taxi].
In this definition, the Greek letter λ marks the concept
[Driver] as the formal parameter. The corresponding
type label Driver is the supertype of the newly defined type
TaxiDriver. In predicate calculus notation, this definition
would be translated to a lambda expression:
TaxiDriver = (λx:Driver)(∃y:Drive)(∃z:Taxi)(Agnt(y,x) ∧ Thme(y,z)).This definition may be read A taxi driver is a driver x for which there exists a driving y and a taxi z where x is the agent of y and z is the theme of drive.
In Figure 10, TaxiDriver and its siblings, BusDriver and TruckDriver, are subtypes of Doer, which is a subtype of Agent. All such types represent temporary roles that last only as long as the agent is performing the corresponding action. An employee of a taxi company who regularly drives taxis might be called a taxi driver when not actually driving a taxi. To distinguish the two roles, different labels should be used: the temporary one might be labeled TaxiDriverAgent; and the more stable one could be labeled TaxiDriverEmployee, which as a subtype of Employee would be under a different branch of Figure 10.
The words role and relation have often been used in conflicting ways in linguistics and computer science. In the KR ontology (Sowa 1984, 2000), they are carefully distinguished: a role is represented by a concept type, such as Mother, Employee, Agent, or Instrument; a relation is represented by a dyadic (or, in general, an n-adic) conceptual relation, such as HasMother, HasEmployee, Agnt, or Inst. When CGs are translated to predicate calculus, roles are represented by monadic predicates, and relations are represented by n-adic predicates. To define relations in terms of roles, there is a primitive dyadic relation type labeled Has, which is used to define a relation such as Agnt in terms of the corresponding role Agent:
Agnt = HasAgent = [Act: λ1]→(Has)→[Agent: λ2].
This definition says that Agnt is a synonym for
HasAgent, which is defined by a dyadic lambda expression
that relates an Act (parameter 1) that has an Agent
(parameter 2). Other relations, such as Ptnt, Rcpt,
and Inst, are defined as synonyms for HasPatient,
HasRecipient, and HasInstrument.
These definitions are not a standard part of the CG logic,
but they are part of the KR ontology, which is commonly
represented and used with conceptual graphs.
In existential graphs, oval enclosures serve two purposes: they mark negations, and they delimit the scope of logical operators. In some versions of EGs, Peirce distinguished the two functions by using the ovals as context delimiters and attaching markers, such as colors or lines of identity, to distinguish the kinds of contexts and their relationships to other entities. In CGs, Peirce's ovals are squared off to form boxes called contexts. Formally, a context is a special case of a concept that contains a nested conceptual graph. Since every context is a concept, it can be linked to conceptual relations in the same way as any other concept. Contexts are one of three kinds of structural elements for building conceptual graphs:
To illustrate the context notation, Figure 11 shows a conceptual graph for the sentence Tom believes Mary wants to marry a sailor. The two nested contexts of Figure 11 are derived from the nested structure of the English sentence, which may be highlighted by using CG context notation to mark the English phrases:
Tom believes [Proposition: Mary wants [Situation: to marry a sailor ]].The type labels of the contexts indicate how the nested CGs are interpreted: what Tom believes is a proposition stated by the CG nested in the context of type Proposition; what Mary wants is a situation described by the proposition stated by the CG nested in the context of type Situation.

Figure 11: A conceptual graph with two nested contexts
The (Expr) relation shows that Tom is the experiencer of a mental state, and the (Thme) relation represents the theme. In the primitive CG notation, a nested CG occurs only inside a concept of type CG or one of its supertypes, such as Graph. When a CG is nested in a concept of type Proposition, the process of type coercion can expand it to a concept of a proposition linked by the statement relation (Stmt) to a concept of a CG that states the proposition. When a CG is nested inside a concept of any other type, such as Situation, two type coercions are invoked as in the following example:
[Situation: [Cat]→(On)→[Mat]] ⇒
[Situation]→(Dscr)→[Proposition]→(Stmt)→[CG: [Cat]→(On)→[Mat]]
The context in the first line represents a situation of a cat on a mat.
On the second line, that context is expanded to a concept of a situation
described by (Dscr) a proposition stated by (Stmt)
a CG that represents a cat on a mat. In effect, a CG nested inside
a context of type CG is a quoted or uninterpreted literal.
A CG nested inside a context of any other type is expanded
by one or two type coercions to a literal inside a concept of type CG.
When a context is translated to predicate calculus, the result depends on the type label of the context. In the following translation, the first line represents the subgraph outside the nested contexts, the second line represents the subgraph for Tom's belief, and the third line represents the subgraph for Mary's desire:
(∃a:Person)(∃b:Believe)(name(a,'Tom') ∧ expr(a,b) ∧ thme(b, (∃c:Person)(∃d:Want)(∃e:Situation)(name(c,'Mary') ∧ expr(d,c) ∧ thme(d,e) ∧ dscr(e, (∃f:Marry)(∃g:Sailor)(agnt(f,c) ∧ thme(f,g))))))If a CG is outside any context, the default translation treats it as a statement of a proposition. Therefore, the part of Figure 11 inside the context of type Proposition is translated in the same way as the part outside that context. But for the part nested inside the context of type Situation, the description predicate dscr is inserted to represent the conceptual relation (Dscr) that would be inserted by type coercion. If a CG were nested inside a concept of type CG, it would be translated to a quoted literal in predicate calculus.
As in Peirce's existential graphs, the context boxes delimit the scope of quantifiers and other logical operators. The sailor, whose existential quantifier occurs inside the context of Mary's desire, which itself is nested inside the context of Tom's belief, might not exist in reality. Following is another sentence that makes it clear that the sailor does exist: There is a sailor that Tom believes Mary wants to marry. In the CG of Figure 12, the concept representing the sailor has been moved outside the two levels of nesting.

Figure 12: A CG that asserts the sailor's existence
The English sentence mentions the sailor before introducing any verb that creates a nested context, and the CG of Figure 12 has an implicit existential quantifier outside any nested context. The corresponding translation to predicate calculus could be derived by moving the quantifier (∃g:Sailor) from the third line of the formula to the beginning of the first line. Another variation, represented by the sentence Tom believes there is a sailor that Mary wants to marry, could be represented by moving the concept [Sailor] into the middle context, which represents Tom's belief. The corresponding formula could be derived by moving the quantifier (∃g:Sailor) to the beginning of the second line.
As Figures 11 and 12 illustrate, the graphic notation for contexts, which is common to the EG, CG, and DRS formalisms, has a considerable advantage in readability. That advantage is especially important for showing the scope of quantifiers and the shifts in meaning when the quantifiers are moved from one context to another. The explicit marking of contexts enables propositions and situations to be treated as first-class entities that can be quantified, referenced by variables or coreference links, and grouped into semantically related collections. That treatment is essential to support metalanguages:
The referent of a concept is some entity or entities in a universe of discourse. The type of referent is specified in a type field, and further information for determining the individual or individuals is specified in a referent field. The individual referent is determined by one of three kinds of signs:

Figure 13: A concept of a cat named Yojo
Neither names nor pictures are primitives in conceptual graphs. Figure 14 shows an expansion of Figure 13 that removes both the name and the picture from the referent field of the concept [Cat]. That CG may be read There is a cat, which has as name the word 'Yojo' and which is described by a picture. The concept [Word: 'Yojo'] represents a word with the character string 'Yojo' as its spelling.

Figure 14: An expansion of the concept in Figure 13
Even the picture is not a primitive, and Figure 14 could be further expanded to the following graph, which shows that the picture is encoded (Encd) as bit string of type JPEG. This CG would not be expanded further because both the bit string and the character string are literals.
[Word: 'Yojo']←(Name)←[Cat]→(Dscr)→[Picture]→(Encd)→[JPEG: '1101...']
The referent field may also contain a universal quantifier ∀, which is read every, or a plural such as {*}@2, which refers to two entities. As an example, Figure 15 shows a conceptual graph that represents the sentence Every cat has as part two ears. In ordinary speech, the qualifier as part is usually omitted, since most people would use background knowlede to determine the particular sense of the verb have.

Figure 15: A CG for the sentence Every cat has two ears.
The universal quantifier in Figure 15 is not a primitive in EGs or CGs. It can always be expanded to an existential quantifier and two nested negations, which can be read as an implication. The expanded CG in Figure 16 may be read If there exists a cat, then it has as part two ears.

Figure 16: Expansion of the universal quantifier in Figure 15.
The plural in Figure 16 is not a primitive CG construct, since it can be represented by a set of cardinality 2, each member of which is an ear. Figure 17 shows a context of type Set, which contains a CG that specifies two members of the set, each of which is an ear that is distinct from (not equal to) the other ear. The cardinality marker @2 is represented by the relation (Card), which links the set to a concept of the integer 2. The referent #this is an indexical that marks a context-dependent referent. In this case, the referent is the concept of type Set in which the indexical is nested. The entire CG in Figure 17 may be read There is a set of cardinality 2; this set has as members one ear and another ear, which are not equal.

Figure 17: A set of two ears
Before the plural referent in Figure 16 can be expanded, it is necessary to determine whether the cat has the two ears collectively or distributively. A collective plural, represented Col{*}@2, would indicate that every cat has as part one set, which contains two ears. A distributive plural, represented Dist{*}@2, would indicate that the cat has two ears as separate parts. Background knowledge about cats and ears would suggest that the distributive interpretation is more likely. With that assumption, two copies of the relation (Part) in Figure 16 would be attached to each of the two concepts of ears in Figure 17 to produce Figure 18.

Figure 18: Expansion of the plural in Figure 16.
A complete expansion that shows each element of a set is only possible for small sets. As an example, the sentence Every trailer truck has 18 wheels, would be represented by the following CG:
[TrailerTruck: ∀]→(Part)→[Wheel: Dist{*}@18].
If fully expanded, the set of wheels would require 162 copies of the
≠ symbol to indicate that each wheel was distinct. For most purposes,
inferences with the CG could be performed without expanding the set.
The unexpanded CG could also be translated
to predicate calculus supplemented with an ontology for sets:
(∀x:TrailerTruck)(∃s:Set)(card(s,18) ∧ (∀w)(memb(s,w) ⊃ ((wheel(w) ∧ part(x,w))).This formula may be read For every trailer truck x, there exists a set s, where the cardinality of s is 18, and for every w, if s has a member w, then w is a wheel and x has w as part. These examples illustrate how short NL expressions map to short CG expressions, which can be systematically expanded to the longer forms represented in predicate calculus.
Natural languages have context-dependent references called indexicals, which are not available in most versions of logic. The referent #this in Figure 17 is an example of an indexical notation that is also used in some object-oriented languages. Natural languages, however, have a much richer variety of indexicals. As an example, the following story uses pronouns, tenses, and cross references that span more than one sentence:
In the basement of a house at 10:17 UTC, there was a cat named Yojo and a mouse. Yojo chased the mouse. Then he caught the mouse. Then he ate the head of the mouse.The time 10:17 UTC and the basement of the house may be assumed as the approximate time and place of the situation described by the entire paragraph. In Figure 19, the concept box of type Situation is linked by the location relation (Loc) to a concept of the basement of a house and by the point-in-time relation (PTim) to a concept of the specified time. Nested inside the large context are three smaller contexts, which contain nested CGs derived from the second, third, and fourth sentences of the paragraph. Each context is linked to the next one by a relation of type Next. At the bottom of Figure 19, the patient relation (PTNT) links [Eat] to [Head]. The theme and the patient relations are both used to link the concept of an action to the concept of the thing that is acted upon. The theme of a verb (e.g. chase or catch) is not changed by the action, but the patient of a verb (e.g. eat) is substantially changed.

Figure 19: Nested contexts with unresolved references
Seven concept nodes in Figure 19 have the indexical marker #, which indicates an unresolved reference. Three concepts of the form [Mouse: #], which may be read the mouse, refer to some previously mentioned mouse — in this example, to the concept [Mouse] in the outer box, which represents the first introduction by the phrase a mouse. The two concepts of the form [Animate: #he] represent the pronoun he. The concepts [Basement: #] and [Head: #] represent the phrases the basement and the head, which do not refer to any previously mentioned basement or head.
Since predicate calculus has no way of marking indexicals, every occurrence of the symbol # must be replaced by a coreference link or label, which can later be translated to a variable in predicate calculus. To mark the first introduction or defining node for an entity, Figure 20 introduces the coreference labels *x for Yojo and *y for the mouse. Subsequent references use the same labels, but with the prefix ? in the bound occurrences of [?x] for Yojo and [?y] for the mouse. The # symbol in the concept [Head: #] of Figure 2 is erased in Figure 20, since the head of a normal mouse is uniquely determined when the mouse itself is identified. The # symbol in the concept [Basement: #] is also erased in Figure 20, since houses rarely have more than one basement.

Figure 20: Nested situations with references resolved
The contexts of conceptual graphs are based on Peirce's logic of existential graphs and his theory of indexicals. Yet the CG contexts happen to be isomorphic to the similarly nested discourse representation structures (Kamp & Reyle 1993). As a result, the techniques developed for the DRS notation can be applied to the CG notation in order to resolve indexicals. After the indexicals have been resolved to coreference labels, Figure 20 can be translated to the following formula in predicate calculus:
(∃s1:Situation)(∃b:Basement)(∃h:House)As this formula illustrates, the four pairs of parentheses that correspond to the context boxes of Figure 20 tend to get lost among the many other uses of parentheses. Well-defined context markers are not only important to aid human readability, but also to support theories of indexicals and methods for resolving them.
(loc(s1,b) ∧ part(h,b) ∧ pTim(s1,"10:17 UTC")
∧ dscr(s1,
(∃s2,s3,s4:Situation)(∃x:Cat)(∃y:Mouse)(name(x,"Yojo")
∧ dscr(s2, (∃u:Chase)(agnt(u,x) ∧ thme(u,y)))
∧ dscr(s3, (∃v:Catch)(agnt(v,x) ∧ thme(v,y)))
∧ dscr(s4,
(∃w:Eat)(∃z:Head)(agnt(w,x) ∧ ptnt(w,z) ∧ part(y,w)))
∧ next(s2,s3) ∧ next(s3,s4)))).
Since conceptual graphs are a highly expressive form of logic, they have been used as a knowledge representation language for nearly every aspect and subfield of artificial intelligence. At the CG workshops and conferences, which have been held annually since 1986, most implementations have addressed several major subfields of AI:
Although CGs can be used for any aspect of an intelligent system, many applications take advantage of the NL features of CGs to support translations between computer-oriented formalisms and natural language input/output. Following are some typical examples:
Great expressive power, which is necessary to represent natural language semantics, allows conceptual graphs to state problems that may be intractable (i.e., require exponential amounts of computing time). Yet computational complexity is not a property of a language, but a property of the problems stated in that language. Furthermore, the complexity class of a problem can be determined by syntactic tests applied to the problem statement. Such tests enable the most efficient CG algorithms to be used for any particular problem:
All versions of classical first-order logic have identical expressive power and model-theoretic semantics. Differences in philosophy, however, have created major differences in the ways that logicians relate logic to language. The two founders of modern logic had diametrically opposed views. With his version of logic, Frege (1879) set out "to break the domination of the word over the human spirit by laying bare the misconceptions that through the use of language often almost unavoidably arise concerning the relations between concepts." Peirce, however, viewed language as the most sophisticated semiotic system ever created by the human spirit and logic as a tool for analyzing and characterizing its structure and operation. Peirce's view of language was extended and deepened by his work as an associate editor of the Century Dictionary, for which he wrote or revised over 16,000 definitions. In summarizing his experience in a letter to the senior editor B. E. Smith, Peirce wrote
The task of classifying all the words of language, or what's the same thing, all the ideas that seek expression, is the most stupendous of logical tasks. Anybody but the most accomplished logician must break down in it utterly; and even for the strongest man, it is the severest possible tax on the logical equipment and faculty.In calling that task "stupendous," Peirce was looking beyond traditional lexicography to a far more ambitious formal ontology with definitions stated in logic.
Frege's animosity toward natural language had the unfortunate effect of leading other logicians, starting with Russell and Carnap, on a century-long neglect of natural language semantics. Even logicians such as Montague, who tried to bring logic and language together, were tainted with a Fregean bias that made language look like a clumsy approximation to predicate calculus. But with his broader and deeper perspective, Peirce provided a surer guide to the central issues of ontology and their expression in both language and logic. Those views affected the design of conceptual graphs in several ways: the most obvious is the adoption of Peirce's graph notation and rules of inference instead of his earlier algebraic notation; next is the adoption of Peirce's ontological categories, which led to design choices that facilitate their expression; and third is the explicit representation of contexts and context-dependent indexicals, which have been ignored in most versions of 20-century logic. The result is a formal system of logic that has a more direct mapping to and from the ontologies implicit in natural language semantics.
Barwise, Jon, & John Perry (1983) Situations and Attitudes, MIT Press, Cambridge, MA.
Croft, William (1998) "Event structure in argument linking," in Butt & Geuder (1998) The Projection of Arguments: Lexical and Compositional Factors, CSLI Publications, Stanford, pp. 21-63.
Cyre, W. R., S. Balachandar, & A. Thakar (1994) "Knowledge visualization from conceptual structures," in Tepfenhart et al. (1994) Conceptual Structures: Current Practice, Lecture Notes in AI 835, Springer-Verlag, Berlin, pp. 275-292.
Cyre, W. R. (1997) "Capture, integration, and analysis of digital system requirements with conceptual graphs," IEEE Trans. Knowledge and Data Engineering, 9:1, 8-23.
Cyre, W. R., J. Hess, A. Gunawan, & R. Sojitra (1999) "A Rapid Modeling Tool for Virtual Prototypes," in 1999 Workshop on Rapid System Prototyping, Clearwater, FL.
Dick, Judith P. (1991) A Conceptual Case-Relation Representation of Text for Information Retrieval, PhD dissertation, Report CSRI-265, Computer Systems Research Institute, University of Toronto.
Esch, J., & R. A. Levinson (1995) "An Implementation Model for Contexts and Negation in Conceptual Graphs", in G. Ellis, R. A. Levinson, & W. Rich, eds., Conceptual Structures: Applications, Implementation, and Theory, Lecture Notes in AI 954, Springer-Verlag, Berlin, pp. 247-262.
Esch, J., & R. A. Levinson (1996) "Propagating Truth and Detecting Contradiction in Conceptual Graph Databases," in P. W. Eklund, G. Ellis, & G. Mann, eds.,
Gentzen, Gerhard (1935) "Untersuchungen über das logische Schließen," translated as "Investigations into logical deduction" in The Collected Papers of Gerhard Gentzen, ed. and translated by M. E. Szabo, North-Holland Publishing Co., Amsterdam, 1969, pp. 68-131.
Gerbé, Olivier, R. Keller, & G. Mineau (1998) "Conceptual graphs for representing business processes in corporate memories," in M-L Mugnier & Michel Chein, eds., Conceptual Structures: Theory, Tools, and Applications, Lecture Notes in AI 1453, Springer-Verlag, Berlin, pp. 401-415.
Gerbé, Olivier, & Brigitte Kerhervé (1998) "Modeling and metamodeling requirements for knowledge management," in Proc. of OOPSLA'98 Workshops, Vancouver.
Gerbé, Olivier (2000) Un Modèle uniforme pour la Modélisation et la Métamodélisation d'une Mémoire d'Entreprise, PhD Dissertation, Département d'informatique et de recherche opérationelle, Université de Montréal.
Halliday, M. A. K., & Christian M. I. M. Matthiessen (1999) Construing Experience through Meaning: A language-based approach to cognition, Cassell, London.
Kamp, H., & U. Reyle (1993) From Discourse to Logic, Kluwer, Dordrecht.
LeClerc, André, & Arun Majumdar (2002) "Legacy revaluation and the making of LegacyWorks," Distributed Enterprise Architecture 5:9, Cutter Consortium, Arlington, MA.
Levinson, R. A. (1996) "General game-playing and reinforcement learning," Computational Intelligence 12:1, 155-176.
Levinson, R. A., & G. Ellis (1992) "Multilevel hierarchical retrieval," Knowledge Based Systems 5:3, 233-244.
Maida, Anthony S., & Stuart C. Shapiro (1982) "Intensional concepts in propositional semantic networks," Cognitive Science 6:4, 291-330.
McCarthy, John (1993) "Notes on formalizing context," Proc. IJCAI-93, Chambéry, France, pp. 555-560.
Montague, R. (1970) "Universal grammar," reprinted in R. Montague (1974) Formal Philosophy, Yale University Press, New Haven, pp. 222-246.
Peirce, C. S. (1880) "On the algebra of logic," American Journal of Mathematics 3, 15-57.
Peirce, C. S. (1885) "On the algebra of logic," American Journal of Mathematics 7, 180-202.
Peirce, C. S. (1909) Manuscript 514, with commentary by J. F. Sowa, available at http://www.jfsowa.com/peirce/ms514.htm
Pustejovsky, James (1995) The generative lexicon, MIT Press, Cambridge, MA.
Rassinoux, Anne-Marie (1994) Extraction et Représentation de la Connaissance tirée de Textes Médicaux, Éditions Systèmes et Information, Geneva.
Rassinoux, A-M., R. H. Baud, C. Lovis, J. C. Wagner, J-R. Scherrer (1998) "Tuning up conceptual graph representation for multilingual natural language processing in medicine," in M-L Mugnier & M. Chein, eds., Conceptual Structures: Theory, Tools, and Applications, Lecture Notes in AI 1453, Springer-Verlag, Berlin, pp. 390-397
Schubert, Lenhart K. (2000) "The situations we talk about," in J. Minker, ed., Logic-Based Artificial Intelligence, Kluwer, Dordrecht, pp. 407-439.
Somers, Harold L. (1987) Valency and Case in Computational Linguistics, Edinburgh University Press, Edinburgh.
Sowa, J. F. (1984) Conceptual Structures: Information Processing in Mind and Machine, Addison-Wesley, Reading, MA.
Sowa, J. F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole Publishing Co., Pacific Grove, CA.
Sowa, J. F. (2003) "Laws, facts, and contexts: foundations for multimodal reasoning," forthcoming.
Stewart, J. (1996) Theorem Proving Using Existential Graphs, MS Thesis, Computer and Information Science, University of California at Santa Cruz.
Van Valin, Robert D., Jr. (1993) "A synopsis of role and reference grammar," in R. D. Van Valin, ed., Advances in Role and Reference Grammar, John Benjamins, Amsterdam, pp. 1-164.
Whitehead, Alfred North (1929) Process and Reality: An Essay in Cosmology, corrected edition edited by D. R. Griffin & D. W. Sherburne, Free Press, New York, 1978.