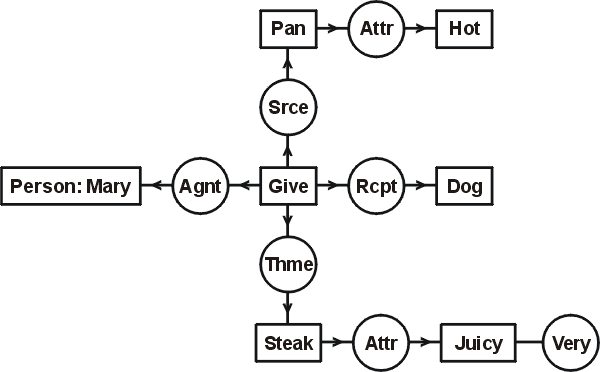
Figure 1: CG for "Mary gives a dog a very juicy steak from a hot pan."
Abstract: Common Logic Controlled English (CLCE) is a formal language with an English-like syntax. Anyone who can read ordinary English can read sentences in CLCE with little or no training. Writing CLCE, however, requires practice in learning to stay within its syntactic and semantic limitations. Formally, CLCE supports full first-order logic with equality supplemented with an ontology for sets, sequences, and integers. The fundamental semantic limitation of CLCE is that the meaning of every CLCE sentence is defined by its translation to FOL; none of the flexibility of ordinary English and none of its metaphorical or metonymic extensions are supported. The primary syntactic restrictions are the use of present tense verbs and singular nouns, variables instead of pronouns, and only a small subset of the many syntactic options permitted in English. Despite these limitations, CLCE can express the kind of English used in software specifications, textbooks of mathematics, and the definitions and axioms of formal ontology.
The design goal for Common Logic Controlled English (CLCE) is to stay as close as possible to precise, carefully written English while supporting automated translation to first-order logic (FOL). The syntax of CLCE is similar to the kind of English used in software documentation and textbooks of mathematics. Anyone who can read English can read CLCE without special training. The hardest part of learning to write CLCE is staying within the semantic restrictions of FOL. Those restrictions are familiar to anyone who has used languages for database query, software design, or formal specification, such as SQL, UML, OWL, Express, and Z. Since those languages can be automatically translated to and from FOL, they can also be translated to and from CLCE. Therefore, CLCE can be used as a readable documentation language that can be compiled to an implementation language. In that regard, CLCE is similar to other controlled languages such as Attempto Controlled English, which is compiled to FOL or to an executable form in Prolog.
Despite its generality, CLCE is not intended to be an official standard; the standard is first-order logic, and CLCE is just a convenient notation for making FOL easier to read and write. Since CLCE has the full expressive power of FOL, it is possible to translate any FOL statement in predicate calculus, CGIF, or many other notations into CLCE. The reverse translation from FOL to CLCE can be automated, but with certain qualifications:
Every prime number less than 3 is even. For every number x, if x is prime, and x is less than 3, then x is even. For every x, if x is a number, x is prime, and x is less than 3, then x is even.If the first sentence were translated to CGs, the reverse translation would produce the original. The second sentence would result from translating the first to typed predicate calculus and back to CLCE. The third sentence would result from translating to untyped predicate calculus and back to CLCE.
To illustrate CLCE, this section presents some examples that show the kinds of sentences that are permitted and their translations to predicate calculus (PC) and the Conceptual Graph Interchange Form (CGIF). The following example has two quantifiers: the universal quantifier every in CLCE, ∀ in PC, and @every in CGIF; and the existential quantifier a in CLCE, ∃ in PC, and a blank in CGIF. It also shows how the verb is links the noun phrase every cat to the prepositional phrase on a mat.
CLCE: Every cat is on a mat. PC: (∀x:Cat)(∃y:Mat)On(x,y) CGIF: (On [Cat: @every] [Mat])
The next example uses some to express the existential quantifier. It also shows the triadic preposition between, which takes a list of two items for its second and third arguments. To avoid possible ambiguities, lists must be enclosed in parentheses.
CLCE: Some person is between a rock and a hard place. PC: (∃x:Person)(∃y:Rock)(∃z:place)(Between(x,y,z) ∧ Hard(z)) CGIF: (Between [Person] [Rock] [Place *z]) (Hard ?z)
Implication in CLCE, which is expressed by the pair of words if and then, is translated to a nest of two negations in PC in order to preserve the scope of quantifiers; the CGIF labels If and Then are defined as synonyms for negated propositions. The definite article the and the functional noun mother represent a function, whose argument is the object of the preposition of. Unlike the word mother, which associates exactly one mother for any child, the word child is a relational noun since a child has two parents and a parent may have multiple children. Every functional noun is also a relational noun, but not all relational nouns are functional.
CLCE: If some person x is the mother of a person y,
then y is a child of x.
PC: ~(∃x:Person)(∃y:Child)
(Mother(x,y) ∧ ~Child(y,x))
CGIF: [If: (Mother [Person *x] [Child *y])
[Then: (Child ?y ?x)]]
This sentence also illustrates the use of variables in CLCE
instead of pronouns. Variables are represented by one of the four
letters x, y, z, or w followed
by an optional string of digits. For readability, any variable may be
preceded by the definite article the and the noun that was used
when the variable was first introduced. Therefore, the previous example
could be rewritten
CLCE: If some person x is the mother of a person y,
then the person y is a child of the person x.
In ordinary English, the many uses of the verb has are indicated by context. In CLCE, those uses are indicated by the word as followed by a relational or functional noun.
CLCE: Every person has some person as mother. PC: ~(∀x:Person)(∃y:person)Mother(y,x) CGIF: (Mother [Person @every] [Person])Note that the verb has and the preposition of represent the focus and argument in opposite order: the subject of has is the argument and the object is the focus of the function or relation.
The next example shows a recursive definition of the relational noun ancestor in terms of parent:
CLCE: Every ancestor of a person x is either
a parent of x or a parent of an ancestor of x.
PC: (∀y)~(∃x:Person)(Ancestor(y,x)
∧ ~(Parent(y,x) ∨
(∃z)(Parent(y,z) ∧ Ancestor(z,x))))
CGIF: [(Ancestor [@lambda] [Person:*x]): @every*y]
[Either: [Or: (Parent ?y ?x)]
[Or: (Parent ?y [*z]) (Ancestor ?z ?x)]]
The translation to CGIF uses a lambda expression for the term,
ancestor of a person x, which states the range
of the universal quantifier. The use of lambda expressions
in conceptual graphs enables an entire noun phrase, including
the quantifier and all the modifiers of the noun to be translated
to a single concept node. A version of predicate calculus that
supported lambda expressions for restricting the range of quantification
could use the same technique; otherwise, a more roundabout paraphrase
is required. For this example, the PC formula would be translated
to the CLCE sentence, For every y, if there is a person x such that
y is an ancestor of x, then either y is a parent of x or there is
a z such that y is a parent of z and z is an ancestor of x.
Although CLCE can only represent singular nouns, collections can be represented by functional nouns such as pair, which can have two arguments, or group and set, which can have an arbitrary list of arguments. As the first line of the following example illustrates, the noun set can be used to represent a functional noun when followed by of and to indicate the type of the focus of the function when used without of.
CLCE: If a set x is the set of (a cat, a dog, and an elephant),
then the cat is an element of x, the dog is an
element of x, and the elephant is an element of x.
PC: ~(∃x:Set)(∃x1:Cat)(∃x2:Dog)(∃x3:Elephant)
(Set(x,x1,x2,x3) ∧ ~(x1∈x ∧ x2∈x ∧ x3∈x))
CGIF: [If: (Set [Set *x] [Cat *x1] [Dog *x2] [Elephant *x3])
[Then: ("∈" ?x1 ?x) ("∈" ?x2 ?x) ("∈" ?x3 ?x)]]
This example shows that when there is only one noun of a given type
in a sentence, the variable may be omitted. The translation to FOL
inserts the implicit variables x1, x2, and x3.
This example and the next also show how English words such as
element and greater can be mapped to mathematical
symbols, such as "∈" and ">".
The syntax of CLCE is patterned after the kind of English used in textbooks of mathematics:
CLCE: For every prime number x,
there is a prime number greater than x.
PC: (∀x:Number)(Prime(x) ⊃
(∃y:Number)(Prime(y) ∧ y>x))
CGIF: [If: (Prime [Number *x])
[Then: (Prime [Number *y]) (">" ?y ?x)]]
Verbs and adjectives can be translated in two ways: a more concise relational representation or a more general and more detailed role representation. In the relational form, a verb such as give is represented by a triadic predicate or relation, and an adjective such as juicy is represented by a monadic predicate. The following example shows the relational representation of a sentence containing a verb and an adjective:
CLCE: Mary gives a dog a juicy steak.
PC: (∃x:Dog)(∃y:Steak)
(Person(Mary) ∧ Give(Mary,x,y) ∧ Juicy(y))
CGIF: (Give [Person: 'Mary'] [Dog] [Steak *y]) (Juicy ?y)
The role representation, which is commonly used in linguistics,
translates give to a monadic predicate or type label,
which is linked to its participants by dyadic relations:
agent (Agnt) for the giver; theme (Thme) for the gift;
and recipient (Rcpt) for the recipient. (See Appendix B
of the book by Sowa (2000) for a
summary of the roles used in linguistics.) Following is the
role representation in both the PC and CGIF notations:
PC: (∃x:Dog)(∃y:Steak)(∃z:Give)(∃w:Juicy)
(Person(Mary) ∧ Agnt(z,Mary) ∧ Rcpt(z,x)
∧ Thme(z,y) ∧ Attr(y,w))
CGIF: [Give *z] (Agnt ?z [Person: Mary]) (Rcpt ?z [Dog])
(Thme ?z [Steak *w]) (Attr ?w [Juicy])
The role representation is more extensible because it allows
any number of modifiers to be added to verbs and adjectives.
The following sentence, for example, could not be represented in the
relational form because the triadic relation for give and
the monadic predicate for juicy leave no room for additional
qualifiers.
CLCE: Mary gives a dog a very juicy steak from a hot pan.
PC: (∃x:Dog)(∃y:Steak)(∃z:Give)
(∃w1:Juicy)(∃w2:Pan)(∃w3:Hot)
(Person(Mary) ∧ Agnt(z,Mary) ∧ Rcpt(z,x)
∧ Thme(z,y) ∧ Attr(y,w1) ∧ Very(w1)
∧ Srce(z,w2) ∧ Attr(w2,w3))
CGIF: [Give *z] (Agnt ?z [Person: Mary]) (Rcpt ?z [Dog])
(Thme ?z [Steak *y]) (Attr ?y [Juicy: *w1]) (Very ?w1)
(Srce ?z [Pan *w2]) (Attr ?w2 [Hot])
An advantage of CGIF is its one-to-one mapping to the display form
of conceptual graphs, as shown in Figure 1. The display form reduces
or eliminates the proliferation of variables by showing relationships
by direct connections.

Figure 1: CG for "Mary gives a dog a very juicy steak from a hot pan."
The CG structure shows why the role representation is more extensible than the relational version. The seven boxes in Figure 1, which are called concept nodes, correspond to the seven variables in PC. The circles, called conceptual relations, correspond to predicates; the arcs attached to a circle correspond to the argument places of the predicate. As Figure 1 shows, the arcs link circles to boxes, not to other circles. The switch from the relational form to the role form replaces the circles for give and juicy with boxes. Then any number of additional relations can be linked to the boxes. The relational form could not be extended by adding new arcs to the circles because arcs do have labels that indicate their types. In the role form, however, the relation labeled Srce, which was added to Give, indicates that the pan is the source. More relations with different labels could be added to indicate the manner or the purpose of the giving.
CLCE is intended as a highly readable supplement to FOL and related languages, such as SQL and UML. Similar techniques can be used to design other controlled languages, such as CLCF, CLCG, or CLCJ for French, German, or Japanese. For all those languages, FOL is the common semantic representation, which can be translated to and from any syntax the user may prefer. To see how CLCE can be used to relate various notations to natural languages and to logic, it is important to consider some examples. Figure 2 shows two structures of blocks and pyramids and their representation in database tables named Objects and Supports. The first step is to declare the syntax of suitable CLCE words and relate them to the two database tables. Then the two structures can be described by CLCE sentences that can be automatically translated to logic, SQL, UML, or other notations.

Figure 2: Two structures represented in a relational database
For this example, CLCE nouns can be represented by relations that are defined by selections from the database tables. The entries in the rows of the tables can be adopted as CLCE names. Following is a declaration of each noun, the predicate or relation that represents it in FOL, and an SQL query that associates the FOL relations with some selection from the database.
Declare object as noun from SQL("SELECT ID FROM OBJECTS"),
shape as functional noun (x1 shape of x2)
from SQL("SELECT SHAPE, ID FROM OBJECTS"),
color as functional noun (x1 color of x2)
from SQL("SELECT COLOR, ID FROM OBJECTS"),
supporter as noun (x1 supporter of x2)
with relation(support) from SQL("SELECT * FROM SUPPORTS"),
supportee as noun (x2 supportee of x1) with relation(support);
The first line of the declaration states that the CLCE word
object is a noun. Its default relation object
is monadic when no variables are stated in the pattern, and
the data that defines the relation is obtained from the SQL statement
enclosed in parentheses. That statement extracts the ID column
from the table named OBJECTS to define object(x).
The next four lines define the words shape
and color as functional nouns represented by dyadic relations,
each of which corresponds to two columns of the OBJECTS table.
The fifth line defines supporter as a relational noun,
whose relation named support contains the complete data
from the database table named SUPPORTS.
The last line defines supportee as a relational noun with
the same support relation, but with the arguments reversed.
The next declaration specifies all the entries in the database tables as CLCE names. In FOL, it is represented by 15 existential quantifiers of the form (∃pyramid:Shape), (∃red:Color), and (∃A:Object). Unlike variables, whose scope is limited to a single sentence or less, names have the entire text as scope.
Declare pyramid, block as name of shape,
red, green, yellow, blue, orange as name of color,
A, B, C, D, E, F, G, H as name of object.
After the nouns and names have been declared, the top structure shown in Figure 2 can be described by the following CLCE sentences. To illustrate the various stylistic options in CLCE, each of the five objects is described with different stylistic conventions.
The shape of A is pyramid; the color of A is red; A is a supporter of D.
Pyramid is the shape of B; green is the color of B; a supporter of D is B.
C has pyramid as shape; C has yellow as color; D is a supportee of C.
D is an object that has block as shape; the object D has blue as color;
a supporter of the supportee E is the supporter D.
The shape of E is pyramid, and the color of E is orange.
Different stylistic choices in CLCE may lead to different representations
in FOL, but they are all logically equivalent. Much of the variation
is reduced or eliminated in the translation from CLCE to FOL,
and the FOL rules of inference can demonstrate the equivalence
of any remaining variability. Following is a line-by-line translation
of the CLCE description to PC formulas:
Shape(pyramid,A) ∧ Color(red,A) ∧ Support(A,D)
Shape(pyramid,B) ∧ Color(green,B) ∧ Support(B,D)
Shape(pyramid,C) ∧ Color(yellow,C) ∧ Support(C,D)
Object(D) ∧ Shape(block,D) ∧ Object(D) ∧ Color(blue,D)
∧ Support(D,E) ∧ Supportee(E) ∧ Supporter(D)
Shape(pyramid,E) ∧ Color(orange,C)
Following are the corresponding conceptual graphs in CGIF notation:
(Shape [:pyramid] [:A]) (Color [:red] [:A]) (Support [:A] [:D])
(Shape [:pyramid] [:B]) (Color [:green] [:B]) (Support [:B] [:D])
(Shape [:pyramid] [:C]) (Color [:yellow] [:C]) (Support [:C] [:D])
(Shape [:block] [Object:D]) (Color [:blue] [Object:D])
(Supports [Supporter:D] [Supportee:E])
(Shape [:pyramid] [:E]) (Color [:orange] [:E])
For this example, none of the stylistic differences have any effect
on either the PC or CGIF representations for objects A, B, C, and E.
For object D, the only difference is the generation of some redundant
type information. Since conceptual graphs are designed to emphasize
the type information, the CGIF form is slightly shorter than the PC
form for object D, and slightly longer for the others. In either case,
the redundant information would be checked for consistency by the rules
of inference; if correct, it would be ignored, and otherwise it would
generate an error message.
The previous declaration statements defined nouns and names that were suffcient to describe the two structures of blocks and pyramids; no verbs, adjectives, or prepositions are needed. However, a logically equivalent description could be stated by representing the database table Supports by the English verb support. The following declaration defines that verb with two patterns for expressing relations in either active voice or passive voice:
Declare support as verb (instrument supports theme)
(theme is supported by instrument)
from SQL("SELECT * FROM SUPPORTS");
In the active pattern, the role instrument (Inst),
which comes before the verb, occurs in subject position,
and the role theme (Thme), which comes after the verb,
occurs in object position. In the passive pattern,
those two positions are reversed: the theme is the subject,
and the instrument is the object of the preposition by.
Those two roles are used in the role representation for verbs;
the presence of two roles in the declaration indicates that
the relation is dyadic.
The SQL statement indicates the source of the data; it may be omitted
if the relation support(x1,x2)
has already been specified by an earlier declaration.
With the verb supports many propositions, such as A supports B, can be stated more simply than with the nouns supporter and supportee. But for some propositions, the nouns can be used to simplify the statements:
For every object x that has orange as color, every supporter of x has block as shape. For every object x that has orange as color, every object that supports x has block as shape.Both of these CLCE sentences are translated to the same form in FOL.
Instead of using the word block as the name of a shape and orange as the name of a color, it may be more convenient to declare block as a special kind of object and to declare orange as an adjective. Those declarations would require more complex SQL statements to define the monadic predicates that correspond to the noun and the adjective:
Declare block as noun
from SQL("SELECT ID FROM OBJECTS WHERE SHAPE='block'"),
orange as adjective
from SQL("SELECT ID FROM OBJECTS WHERE COLOR='orange'").
With these declarations, the previous statements become
For every orange object x, every supporter of x is a block. For every orange object x, every object that supports x is a block.The current version of CLCE prohibits universally quantified noun phrases from being used as the object of a preposition. Without that restriction, the previous statement could have been simplified further:
Every supporter of every orange object is a block.These statements could be derived by data mining programs, which search for generalizations found in the database, or they could be stated as constraints enforced by restrictions on permissible updates.
These examples show how CLCE can be related to a relational database by means of the keyword SQL in the declarations. The SQL syntax is not recognized by the CLCE processor, which merely passes the quoted SQL statement to an interface program that links CLCE to the database. Other keywords, such as UML or URI, could be used to link CLCE to data from UML definitions or from resources located anywhere on the Internet.
Unlike English, for which background knowledge is required to resolve many ambiguities, CLCE has a syntax that allows every ambiguity to be resolved when a sentence is parsed. The declarations that are necessary for translating CLCE to FOL can also be used at parse time in order to select the correct sense for each word and generate the translation to other notations. Following is a summary of the kinds of ambiguities that occur in English and the CLCE restrictions used to avoid them:
The option of attaching prepositional phrases to many different parts of speech was avoided in classical Latin by the same restriction used for CLCE: prepositions could only be attached to a verb or to a participle derived from a verb. In English, the multiple possibilities can confuse a native speaker, as in the following sentence:
Bob sees the man on the hill with a telescope.The preposition on could be attached to either the verb sees, or the noun man and the preposition with could be attached to sees, man, or hill. In CLCE, the only preposition that can be attached to a noun is of. Therefore, the only permissible interpretation is that the seeing takes place on the hill and with a telescope. The other possibilities can be expressed in CLCE with relative clauses:
Bob sees the man that is on the hill with a telescope. Bob sees the man on the hill that is with a telescope. Bob sees the man that is on the hill that is with a telescope. Bob sees the man that is on the hill and is with a telescope.Although all five sentences are unambiguous in CLCE, the first three might be confusing to an English speaker who was not familiar with the CLCE conventions. Therefore, they can be expressed in a way that is unambiguous in both CLCE and ordinary English:
On the hill, with a telescope, Bob sees the man. With a telescope, Bob sees the man that is on the hill, On the hill that is with a telescope, Bob sees the man.Although computers are not as good as people at resolving ambinguities, they are much better than people at detecting ambiguities. Therefore, it is possible to design CLCE writing tools that check for CLCE sentences that might be ambiguous in ordinary English and suggest possible paraphrases that are unambiguous in both CLCE and English.
Some English verbs can have an associated preposition of, such as consists of and talks of, Fortunately, those verbs do not have a direct object. To avoid possible ambiguities, no verbs in CLCE that take a preposition of may also have a direct object. The verb tells, which takes a direct object, could be declared in a pattern with the preposition about, but not of.
The sentences of CLCE resemble a subset of the sentences of ordinary English. Like English sentences, each CLCE sentence has one or more clauses, and each clause has one main verb. A sentence can be classified in two ways: according to its structure, a sentence may be simple, complex, or compound; according to its use, a sentence may be declarative, interrogative, or imperative. Following are some examples:
Yojo is a cat. Mary gives a dog a very juicy steak from a hot pan.
Every cat that is on a mat is happy. If a number is even, then the number is not odd.
Some cat is on a mat, the cat is orange, and the mat is blue. For every integer, either the integer is even, or the integer is odd.Some compound sentences such as these can be restated as simple sentences:
Some orange cat is on a blue mat. Every integer is either even or odd.When both versions of the CLCE sentences are translated to predicate calculus and CGIF, the results are identical or have minor variations. The PC translations for the two sentences about integers are identical, and the translations about the cat differ only in the order of the predicates:
(∃x:Cat)(∃y:Mat)(On(x,y) ∧ Orange(x) ∧ Blue(y)) (∃x:Cat)(∃y:Mat)(Orange(x) ∧ Blue(y) ∧ On(x,y))
What even number is smaller than 3? If every cat that is on a mat is happy, is it true that some cat that is not happy is on a mat?
Import 'http://www.jfsowa.com/verbs/give.clc'. Declare give as verb (agent gives recipient theme) (agent gives theme to recipient) (theme is given recipient by agent) (theme is given to recipient by agent) (recipient is given theme by agent). Note: This is a comment, which is ignored by the system.
A sequence of sentences separated by semicolons is called an extended sentence. The primary purpose of a extended sentence is to allow the scope of variables and quantifiers to extend beyond a single sentence. In the following example, the first noun prhase is translated to an existential quantifier, such as (∃x:Number). In the next sentence, the referential noun phrase the number is represented by a reference to the same variable x.
An even number greater than 6 is less than 9; what is the number?A period or question mark at the end of the last sentence terminates the scope of all quantifiers in the extended sentence. The rules for the scope of quantifiers and the variables they govern are discussed in Section 6.
CLCE words are divided into a small number of reserved words and an open-ended number of declared words. All reserved words are spelled like English words, but their meanings are restricted to just one word sense or to a small number of senses that can be distinguished by the syntax. There are ten kinds of reserved words:
Declared words can represent names, nouns, verbs, adjectives, adverbs, or prepositions. They may be words with the same spelling as English words, words combined with underscores such as hard_disk_drive, or arbitrary sequences of letters, digits, and underscores. Before a word can be used in CLCE, its syntax and its mapping to a relation in FOL must be specified by a declaration.
A name is a word that refers to some entity called its referent. CLCE names are represented by character strings enclosed in single quotes; any single quote appearing in a name must be doubled, as in 'O''Reilly'. If the only characters that appear in a name are letters, digits, and underscores, the enclosing quotes may be omitted.
Names can be declared in a declaration, which is an imperative sentence that begins with the verb declare. That declaration can also state a monadic predicate that is true of the entity to which the name refers.
Declare 'Grand Central Terminal' as name of building,
Yojo as name of cat,
Sue as name of woman.
The names Yojo and Sue are represented by existential
quantifiers (∃Yojo:Cat) and (∃Sue:Woman).
A name that contains special characters is translated to an internally
generated name that begins with an underscore and does not contain
any special characters:
(∃_GrandCentralTerminal:Building)
(_GrandCentralTerminal='Grand Central Terminal')
The scope of these names is the entire text in which the declaration
occurs. After a name has been declared in a text, it can be used
at any subsequent sentence in the text as a complete noun phrase
by itself.
A name can also be declared by a noun phrase that begins with the definite article the. The following sentence declares the same three names as the previous declaration, and it also asserts a relationship about their referents:
The woman Sue sees the cat Yojo in the building 'Grand Central Terminal'.The three names are represented in FOL in the same way and with the same scope as if they had occurred in a declaration. If the names had already been declared, the same proposition could be asserted by using the names without adding the article the or a noun such as cat:
Sue sees Yojo in 'Grand Central Terminal'.After a name has been declared, it can be used at any subsequent point in the same text. It may occur as a complete noun phrase by itself, or it may be prefixed with the definite article the and the noun that specifies the predicate that is true of its referent.
Two kinds of entities, integers and character strings, have special names that do not have to be declared because the syntax of the name uniquely determines the referent and its type:
In addition to the names whose scope is the entire text, there are temporary names called variables, whose scope is limited to a single sentence or less. A variable is any name that consists of one of the letters x, y, z, or w followed by an optional string of digits. At its first occurrence in a sentence, a variable must occur in either an existential noun phrase, which begins with an existential quantifier, or a universal noun phrase which begins with universal quantifier. In subsequent occurrences within the sentence, the variable may occur by itself or in a noun phrase such as the set x. For further discussion of variables, see Section 6 on scope of quantifiers.
Unlike a name, which refers to a particular entity in the subject domain or universe of discourse, a common noun may refer to any entity of a given type. CLCE supports four kinds of common nouns: categorial nouns, relational nouns, functional nouns, and variadic relational or functional nouns. All of these nouns can be represented in FOL by type labels and predicates or relations.
Declare dog as noun,
table as noun,
hound as noun with relation(dog).
The default representation for a noun is a monadic predicate or
a type label with the same spelling as the noun; the declaration
of hound shows how a predicate with a different spelling
is declared. As a result, both nouns dog and hound
are represented by the same predicate: dog(x).
Declare child as noun (x1 child of x2),
employee as noun (x1 employee of x2),
In this declaration, the parenthesized expressions are patterns
that indicate how the noun is used in a CLCE sentence. The two variables
x1 and x2 indicate that each noun is represented
by a dyadic relation.
In this example, the variable x1 indicates the focus,
but in the following example, x2 indicates the focus:
Declare parent as noun (x2 parent of x1) with relation(child),
employer as noun (x2 employer of x1) with relation(employee).
By switching the focus and correlative, the same two relations
child(x1,x2) and employee(x1,x2) can be used
to define the relational nouns parent and employer.
Declare mother as functional noun (x1 mother of x2),
sum as functional noun (x3 sum of x1 and x2) with relation("+").
In line 1, mother is defined in the same way as child,
but with the additional qualifier functional.
In line 2, sum is defined by a triadic relation whose
spelling is the special symbol "+", which must be enclosed
in quotation marks. The pattern indicates that the focus
of the function, also called its result,
is the third argument of the relation.
Declare set as functional noun (x1 set of x2 ...).The next sentence declares empty_set as a name of a set and says that nothing is an element of it:
Nothing is an element of the set empty_set.In the translation to FOL, the word nothing is represented by a negated existential quantifier with no type label ~(∃x). The absence of a type label means that the quantifier ranges over everything in the universe of discourse.
PC: (∃empty_set:Set)~(∃x)(x ∈ empty_set)
CGIF: [Set: empty_set] ~[("∈" [*x] [: empty_set])]
Since all names have global scope, the declaration of empty_set
as a name forces its existential quantifier to be moved to the front.
The existential quantifier for a variable would remain
within the scope of the negation.
The problem of determining the referents of pronouns and other referential noun phrases is intimately connected with the question of the scope of quantifiers in first-order logic. As examples, consider the following CLCE sentences:
Bob sees a car; the car is red. Bob does not see a car; the car is red.In the first line, the phrase, a car, is represented by an existential quantifier, (∃x:Car), in the sentence before the semicolon. In the sentence after the semicolon, the referential noun phrase, the car, which is represented by the variable x, is associated with the car that is assumed to exist. But the car that Bob does not see is represented by an existential quantifier within the scope of a negation. Therefore, it is not possible to refer to the car after the semicolon because its identity and even its existence are in doubt. That example illustrates two fundamental principles:
CLCE grammar rules are written in Extended Backus-Naur Form (EBNF), as specifed by International Standard ISO/IEC 14977. Each EBNF rule is preceded by an informal English paraphrase. In any question of interpretation, the EBNF rule takes precedence over the English statement. This section uses EBNF to define three kinds of grammar rules for CLCE: lexical rules, which define the categories of words that occur in CLCE sentences; syntactic rules, which define the combinations of words in phrases and sentences; and declaration rules, which define the statements that declare CLCE words and their mapping to FOL or other notations.
CLCE lexical rules define the permissible combinations of characters that may occur in words, names, varibles, integers, and character strings.
Adjective = Word;
CharString = """", {Character - """" | """"""}, """";
Comparative = Word;
Ellipsis = "...";
Exponent = ("e" | "E"), ["+" | "-"], UnsignedInt;
Floating = ["+" | "-"], ( ".", UnsignedInt, [Exponent]
| UnsignedInt, ( ".", [UnsignedInt], [Exponent]
| Exponent));
FunctionalNoun = Word;
Integer = ["+" | "-"], UnsignedInt;
Name = QuotedName | Word;
Noun = Word;
Number = Integer | Floating;
Preposition = Word;
QuotedName = "'", {Character - "'" | "''"}, "'";
RelationalNoun = Word;
UnsignedInt = Digit, {Digit};
Variable = ("x" | "X" | "y" | "Y" | "z" | "Z" | "w" | "W"), {Digit};
Verb = Word;
Word = (((Letter | Digit | "_"), {Letter | Digit | "_"})
- Variable) - Integer;
The CLCE grammar can be parsed in linear time by a recursive-descent parser without backtracking. One or more whitespace characters may be inserted between any syntactic constituents; words and numbers must be separated by at least one whitespace character, but whitespace is optional before and after punctuation. Unlike English, which allows different styles for the placement of commas, CLCE commas are required in some cases where they would be optional in English. The major difference between English and CLCE punctuation is that CLCE requires parentheses around lists with more than two elements and around deeply nested compound and complex sentences.
Comparison = Comparative, "than", SimpleNP;
ComplexDS = Conditional, ", then", ParenDS
| ParenDS, ( "only", Conditional
| "if and only", Conditional);
CompoundDS = ParenDS, "," {ParenDS, ","}, "and", ParenDS
| "either", ParenDS, "," {ParenDS, ","}, "or" ParenDS;
Conditional = "if", Declarative;
Declarative = {LogPrefix}, (SimpleD | ComplexD | CompoundD);
ExistentialNP = ("something" | "someone"), [Variable]
| "the", FunctionalNoun, [Variable], "of", List
| ("a" | "an" | "some"), Term;
ExtendedSentence = Declarative, {";", Declarative} ".";
| Imperative, {";", Imperative} ".";
| {Declarative, ";"}, Interrogative, {";" Interrogative}, "?";
GeneralName = Name | Variable | Number | CharString;
Interrogative = [Conditional, ","],
( WhPhrase, VerbP
| "is it true that", Declarative);
List = SimpleNP, ["and", SimpleNP]
| "(", SimpleNP, ",", {SimpleNP, ","},
( Ellipsis
| "and", ("others" | "nothing else" | "no one else" | SimpleNP)), ")";
LogPrefix = "for", UniversalNP, ","
| "there is", ExistentialNP, "such that"
| "it is false that";
NegExistentialNP = ("nothing" | "no one"), [Variable]
| "no", (Term | FunctionalNoun, [Variable], "of", List);
NounP = ExistentialNP
| UniversalNP
| NegExistentialNP
| ReferentialNP;
ParenDS = {LogPrefix}, (SimpleDS
| "(", ComplexDS, ")"
| "(", CompoundDS, ")" );
Postmodifer = (Comparison | "that", VerbP);
PredComp = ["not"], (Adjective | SimpleNP | Comparison | PrepositionalP);
PrepositionalP = Preposition List;
ReferentialNP = GeneralName
| "the", (Noun | RelationalNoun | FunctionalNoun),
[GeneralName];
Sentence = Declarative | Interrogative | Imperative;
SimpleDS = {PrepositionalP - ("for", SimpleNP), ","}, NounP, VerbP
| "there is", (ExistentialNP | NegExistentialNP);
SimpleNP = ExistentialNP | ReferentialNP
SimpleVP = "is", ( PredComp, ["and" PredComp]
| "either", PredComp, {",", PredComp},
[","], "or", PredComp;
| ("has" | "does not have"), SimpleNP,
"as", (RelationalNoun | FunctionalNoun);
| (VerbSing | "does not", VerbInf),
[SimpleNP, [SimpleNP]], {PrepositionalP}
| "is", ["not"], VerbPastPart, [SimpleNP], {PrepositionalP};
Term = {Adjective},
( RelationalNoun, [Variable], "of", List
| Noun, [Variable], [Postmodifier]);
Text = {ExtendedSentence | Heading};
UniversalNP = ("everything" | "everyone"), [Variable]
| "every", Term;
VerbP = SimpleVP ["and", SimpleVP]
| "either", SimpleVP, {",", SimpleVP}, [","], "or", SimpleVP
| "is", PredComp, "and" PredComp
| "is", "either", PredComp, {",", PredComp}, [","], "or", PredComp;
WhPhrase = ("who" | "what" | "when")
| "which", Term;
Translation from CLCE to first-order logic in any notation is based on the same general principles. The translation is somewhat simpler for conceptual graphs, which have been designed to map to and from natural languages as directly as possible, but the initial stages of generating any other notation for FOL are the same. The only difference is that a few extra steps are needed in the final stages for generating predicate calculus and other notations. Following is a summary of the basic principles:
To illustrate the translation, consider the sentence Every cat is on a mat, which is translated to predicate calculus in the following steps. For clarity in the presentation, these steps are written sequentially in this example, but they can be carried out in a single pass through the text.
(∀x:cat) is on (∃y:mat).
(∀x:cat)(∃y:mat)(x is on y).
To illustrate the treatment of negations, consider the sentence Every cat is not on a mat:
(∀x:cat) is not on (∃y:mat).
(∀x:cat)(∀y:mat)(x is not on y).
(∀x:cat)(∀y:mat)~on(x,y).
The same proposition could be expressed with the quantifier no, as in No cat is on a mat.
~(∃x:cat) is on (∃y:mat).
(∀x:cat)(∀y:mat)~(x is on y).
(∀x:cat)(∀y:mat)~on(x,y).
First-order logic is sufficiently expressive to specify a Turing machine, any digital computer, or any software that could be implemented on a digital computer. It is also sufficiently expressive to specify a Petri net or any system of times, events, and causal sequences that may be modeled by a Petri net. A specification that is limited to nothing but pure FOL, however, can become encrusted with so much detail that no amount of "syntactic sugar" can make it understandable. For that reason, many extensions beyond classical FOL are necessary to make such specifications not only possible, but readable and understandable.
Copyright ©2004 by John F. Sowa. Permission is hereby granted for anyone to make verbatim copies of this document for teaching, self-study, or other noncommercial purposes provided that the copies cite the author, the URL of this document, and this permission statement. Please send comments to John Sowa.
Last Modified: