
Figure 1: Relating a theory to the world
One of the oldest controversies about Aristotle's categories was whether they represent the kinds of things that exist or the way people perceive, think, and talk about things that exist. Theophrastus, Aristotle's successor as head of the Lyceum, said that the categories were intended in all those ways — in modern terms, ontological, epistemological, and lexical. Today, the fragmented treatments of those subjects are scattered across the fields of philosophy, linguistics, and artificial intelligence, in each of which the researchers who work with formal representations or informal techniques tend to cluster in disjoint sets. Yet natural languages are capable of expressing and reasoning about both kinds of information: anything that can be expressed in the most precise formal logic ever invented can be paraphrased in any natural language; conversely, a three-year-old child has the ability to learn, imagine, and express ideas that are far beyond the most sophisticated computer systems available today.
The limitations of current systems have been discussed in the article on The Challenge of Knowledge Soup. As a companion piece, this article is a tutorial about formal theories and their relationships to language and the world. It has been assembled as a series of extracts from several published papers that have been modified and pieced together. The references can be found in the combined bibliography for this web site. There is also a PDF version for more convenient printing.
As an example of the controversies, Gangemi et al. (2003) maintain that the terms vase and lump of clay have different identity criteria; therefore, they imply two distinct objects that happen to occupy the same location. Others maintain that the distribution of matter takes precedence over any method of describing it: if two descriptions characterize the same matter, they must describe the same object. In terms of his theory of signs, Peirce would say that anything can be described in any number of ways from any perspective for any purpose. The particular choice of words or other signs depends on the intentions of some viewer who might choose one perspective rather than another. That choice is not purely subjective, since there are objective, but species-specific criteria for preferring one to another (Deely 2003). A bee, for example, might ignore the vase and focus on the flowers in the vase, while a dog might push the flowers aside and drink the water that some human had put there for a very different purpose. Each perspective depends on the intentions of some individual of some species, and any question about the priority of one perspective over another cannot be answered without considering the intentions of the questioner.
The problems of knowledge soup result from the difficulty of matching theories based on discrete concepts to the continuous physical world. Methods of fuzziness, probability, defaults, revisions, and relevance represent different ways of measuring, evaluating, or accommodating the inevitable mismatch. Each technique is a metalevel approach to the task of finding or constructing a theory and determining how well it approximates reality. To bridge the gap between theories and the world, models are Janus-like structures, with an engineering side facing the world and an abstract side facing the theories (Figure 1).

Figure 1: Relating a theory to the world
On the left is an icon of the physical world, which contains more detail and complexity than any humanly conceivable model or theory can represent. In the middle is a mathematical model that represents a domain of individuals D and a set of relations R over D. If the world had a unique decomposition into discrete objects and relations, the world itself would be a universal model, of which all accurate models would be subsets. But as the examples of knowledge soup have shown, the selection of a domain and its decomposition into objects depends on the intentions of some agent and the limitations of the agent's measuring instruments. The degree of precision or vagueness of a true proposition depends on the adequacy of the correspondence between the model and the world. Tarski's logical models can never be vague, but they are always approximations. Even the best models are approximations to a limited aspect of the world for a specific purpose. As the engineer and statistician George Box (2005) said, "All models are wrong; some models are useful."
The two-stage mapping from theories to models to the world replaces the direct mapping of sentences to the world as characterized by two diametrically opposed views of semantics: Tarski's version of model theory, and the version of fuzzy logic by Lotfi Zadeh (1975). In Tarski's approach, each sentence has two possible truth values: {true, false}. In fuzzy logic, a sentence may have a continuous range of possible values from 0.0 for certainly false to 1.0 for certainly true; intermediate values would represent hedging terms, such as likely, unlikely, very nearly true, or almost certainly false.
Susan Haack (1978, 1996) was one of the early critics of fuzzy logic, who has continued to sharpen her arguments against the claims that natural language justifies or even requires "degrees of truth." Her most serious criticism is not that fuzzy logic is vague, but that it is too precise: instead of modeling the way people talk and think about vagueness, fuzzy logic forces an unwarranted quantification of vagueness. The two-stage mapping of Figure 1, however, makes room for both kinds of reasoning: a rigorous two-valued logic for evaluating the truth of a mathematical theory in terms of a model; and a continuum of fuzzy values that measure the suitability of a particular model for a particular purpose in actions upon the world. Such two-stage mappings have long been used in science and engineering: a two-valued logic for mathematical reasoning, and a continuum of values for estimating the experimental error.
The axioms and definitions associated with any category of an ontology are inherited through the hierarchy from more general categories at the upper levels to more specialized subcategories or subtypes at lower levels. The theories associated with those categories can also be organized in a hierarchy. Figure 2 shows a small excerpt from the infinite hierarchy of all possible theories. Each theory is a generalization of the ones below it and a specialization of the ones above it. The top theory contains all tautologies — all the logically true propositions, such as p⊃p, which are provable from the empty set of axioms. Each theory below the top is derived from the ones above it by adding more axioms. Its theorems include all the theorems inherited from above plus all the new ones that can be proved from the new axioms or from their combination with the inherited axioms.

Figure 2: A generalization hierarchy of theories
Just below Tautologies are four theories named Antisymmetry, Transitivity, Reflexivity, and Symmetry, each of which inherits all the propositions from the theory named Tautologies. In addition, each of those theories adds one relation R and one axiom that characterizes R:
Adding axioms makes a theory larger, in the sense that more propositions become provable. But the larger theory is also more specialized, since it applies to a smaller range of possible models. This principle, which was first observed by Aristotle, is known as the inverse relationship between intension and extension: as the meaning or intension grows larger in terms of the number of axioms or defining conditions, the extension grows smaller in terms of the number of possible instances. As an example, more conditions are needed to define the type Dog than the type Animal; therefore, there are fewer instances of dogs in the world than there are animals. Even more axioms are needed to define the subtypes Dachshund or Collie, which have even fewer instances than the type Dog.
The theory named Equivalence has three axioms, which it inherits from the theories of Reflexivity, Symmetry, and Transitivity. The symbol R could be replaced by many other labels to distinguish various kinds of equivalence relations. For example, if the domain of x and y is the set of all animals, then R(x,y) could mean that x was born under the same sign of the zodiac as y. If Charlie and Snoopy had birthdays under the same sign, R(Charlie,Snoopy) would be true. The usual equality operator = satisfies these axioms, and so does the operator ≡ for logical equivalence.
The theory named PartialOrder in Figure 2 inherits the axioms of Reflexivity, Transitivity, and Antisymmetry. In set theory, the subset relation x⊂y is a partial order, and so is the ≤ relation for numbers. When applied to the domain of individual statements in logic, the operator for material implication, x⊃y, is not a partial order because it violates the axiom for antisymmetry, and it's not an equivalence relation because it violates the axiom for symmetry. The next two examples illustrate those violations:
The word hierarchy, which originally referred to the nine orders of angels, is now used as an informal term for any partial order. The term tangled hierarchy is sometimes used for a partial order that differs from a tree by having cross links. Any binary relation can be represented as a graph, and every graph that represents a partial order is acyclic. Figure 3 shows three examples: a lattice, a tree, and an irregular acyclic graph that is neither a tree nor a lattice.

Figure 3: Three acyclic graphs
When a partial-order relation, such as x≤y, is represented by a graph, some convention is needed to distinguish x from y. One common convention, which is used in Figure 2, is to place x at a lower level than y. Another common convention is to draw an arrowhead directed from x to y. Figure 3 uses both conventions to represent the graphs for three partial orders.
There are many variations of trees, but the one illustrated in Figure 3 is a rooted tree, which is a mathematical structure consisting of a set T, a partial-order operator ≤, a special element of r of T called the root, and two axioms in addition to the three that define a partial order:
A lattice is a mathematical structure consisting of a set L,
a partial-order operator ≤, and two dyadic
operators  and
and  .
If x and y are elements of L,
x
.
If x and y are elements of L,
x y is called
the greatest lower bound or infimum of x
and y,
and x
y is called
the greatest lower bound or infimum of x
and y,
and x y is called the
least upper bound or supremum of x and y.
If L is a lattice of sets,
the symbol ≤ is the subset operator,
y is called the
least upper bound or supremum of x and y.
If L is a lattice of sets,
the symbol ≤ is the subset operator,
 is the intersection operator,
and
is the intersection operator,
and  is the union operator.
For any x, y, and z in L,
these operators satisfy the following axioms:
is the union operator.
For any x, y, and z in L,
these operators satisfy the following axioms:
 y
≤ x and
x
y
≤ x and
x y
≤ y.
y
≤ y.
 y.
y.
 y and
y ≤
x
y and
y ≤
x y.
y.
 y
≤ z.
y
≤ z.
A bounded lattice has a top  and a bottom
and a bottom
 . For any element x in a bounded
lattice,
. For any element x in a bounded
lattice,  ≤ x
≤
≤ x
≤  .
All finite lattices are bounded, and so are many infinite ones.
For a lattice of subsets,
.
All finite lattices are bounded, and so are many infinite ones.
For a lattice of subsets,
 is a universal set U,
and
is a universal set U,
and  is the empty set {}.
is the empty set {}.
Every tree and every lattice is acyclic, but the only graphs that are both trees and lattices are the chains, which consist of a single path from beginning to end. In fact, chains represent a special case of a partial order called a linear order. Since chains and trees have a unique path from any node to the top, they support single inheritance of axioms or other properties. Acyclic graphs that permit multiple paths support multiple inheritance. In programming languages, multiple inheritance may lead to conflicts among inconsistent properties inherited along different paths. A lattice, however, is a well-disciplined hierarchy, which can aid in the detection and prevention of inconsistencies.
An infinite collection of all possible theories would bear an uncanny resemblance to "The Library of Babel" envisioned by the poet, storyteller, and librarian Jorge Luis Borges (1941). His imaginary library consists of an infinite array of hexagonal rooms with shelves of books containing everything that is known or knowable. Unfortunately, the true books are scattered among infinitely many readable but false books, which themselves are an insignificant fraction of the unreadable books of random gibberish. In the story by Borges, the library has no catalog, no discernible organization, and no method for distinguishing the true, the false, and the gibberish. In a prescient anticipation of the World Wide Web, Borges described people who spend their lives aimlessly searching through the rooms with the hope of finding some hidden secrets. But no matter how much truth lies buried in such a collection, it is useless without a method of organizing, evaluating, indexing, and finding relevant books and the theories contained in them.

Figure 4: The Library of Babel by Borges
An infinite hierarchy without an index or catalog might contain all the theories that anyone would ever want or need, but no one would be able to find them. To organize the hierarchy of theories, Tarski's student Adolf Lindenbaum showed that the theories could be arranged along the well-defined paths of a lattice. If the theories are expressed in first-order logic, the partial ordering X≤Y could be interpreted in three different ways, each of which defines exactly the same lattice:
 Q.
Q.
 Q.
Q.
The reason why implication defines a partial order over theories, but only a preorder over propositions is that two propositions or two sets of axioms can be logically equivalent, but not identical. A theory T, however, may be defined as the deductive closure of some axioms S:
T = closure(S) = {p | SThe theory T, the deductive closure of the axioms S, is the set of all propositions p that are provable from S. If two propositions or two sets of axioms are logically equivalent (in the sense that each one implies the other), then their closures are exactly the same theory. Therefore, implication over theories satisfies the axiom of antisymmetry in addition to the axioms for a preorder.p}
The traditional mathematical theories illustrated in Figure 2 are a small part of the infinitely many theories that could be specified by axioms in any version of logic. When extended to all possible theories, the complete hierarchy is sufficient to formalize all the computer programs that have been written or ever will be written by humans, robots, compilers, or AI systems. Besides the elegant theories that mathematicians prefer to study, the hierarchy contains truly "ugly" theories for the poorly designed and undebugged programs that even their authors would disown. Whether ugly or elegant, any program can be specified by some theory that defines the results computed by the program for any given combination of inputs.
The lattice operators define a systematic network for inheriting axioms, combining theories, and searching for new ones. The techniques of nonmonotonic logic depend on metalevel reasoning about exceptions, defaults, consistency, abnormality, priorities, or the failure to prove. Instead of using nonmonotonic logic, many philosophers, logicians, and computer scientists, such as John McCarthy (1977), Isaac Levi (1980), and Peter Gärdenfors (1988), have maintained that it is conceptually simpler to use first-order logic and adopt explicit metalevel methods for reasoning about the axioms of a theory. The process of theory revision or belief revision is a metalevel method for modifying axioms to construct a new theory that forms a better match to a given collection of facts. Partisans of nonmonotonic logic and theory revision have repeatedly demonstrated that new methods proposed for one approach can be converted to logically equivalent methods for the other approach.
Methods of theory revision can be interpreted as techniques for navigating an infinite lattice of first-order theories. From each theory, the partial ordering of the lattice defines paths to more general theories above and more specialized theories below. Figure 5 shows four basic ways of moving along the paths from one theory to another: contraction, expansion, revision, and analogy. The first three operators are defined by the AGM axioms (Alchourrón et al. 1985); the fourth operator, which revises a theory by renaming the labels of types and relations, was defined by Sowa (2000).
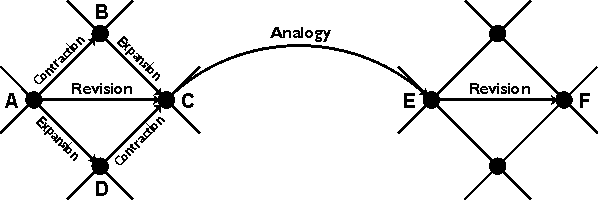
Figure 5: Navigating the lattice of theories
To illustrate the moves through the lattice, suppose that theory A is Newton's theory of gravitation applied to the earth revolving around the sun and that F is Niels Bohr's theory about an electron revolving around the nucleus of a hydrogen atom. The path from A to F is a step-by-step transformation of the old theory to the new one. The revision step from A to C replaces the gravitational attraction between the earth and the sun with the electrical attraction between the electron and the proton. That step can be carried out in two intermediate steps:
By repeated application of the four operators in Figure 5,
any theory or collection of beliefs can be converted to any other.
Multiple contractions would reduce a theory to the empty
or universal theory  at the top,
which contains only the tautologies that are true of everything.
Multiple expansions would lead to the inconsistent or
absurd theory
at the top,
which contains only the tautologies that are true of everything.
Multiple expansions would lead to the inconsistent or
absurd theory  at the
bottom of the lattice, which contains all axioms and is true of nothing.
The analogy operator allows shortcuts that can jump across the lattice
by a systematic relabeling of the types and relations.
If the original theory is consistent, the analogy must also be consistent,
since the axioms are identical except for a change of names.
at the
bottom of the lattice, which contains all axioms and is true of nothing.
The analogy operator allows shortcuts that can jump across the lattice
by a systematic relabeling of the types and relations.
If the original theory is consistent, the analogy must also be consistent,
since the axioms are identical except for a change of names.
Each step through the lattice of theories is simple in itself, but the infinity of possible steps makes it difficult for both people and computers to find the best theory for a particular problem. Newton became famous for discovering the axioms that explain the solar system, and Bohr won the Nobel Prize for revising them to explain the atom.
The lattice of theories is much better organized than the uncataloged library of Babel, but it shows only the possible pathways. It does not explain why anyone should prefer one path to another. In science, a theory is more than a collection of propositions. To be meaningful, it must have applications and explanatory power:
For any natural language, dictionaries list many different senses for each word, but no two dictionaries list exactly the same senses. The English word file, for example, is derived from two homonyms: a Germanic word for a tool used for smoothing or scraping, and the Latin word filum for thread. All dictionaries recognize that split, but the senses on either side of the split depend on subtle variations from one application to another. Since English has the word thread for the original meaning of filum and the technical word filament for thread-like things, the remaining meanings derived from filum represent various metaphors and metonyms, such as people walking in a single line or documents arranged on a string or wire. As the technology evolved, the wire was replaced by boxes of cards, whose contents were later copied to magnetic tape. In computer systems, the word file now refers to a linear order of bits, bytes, lines, or records on any storage medium.
Formal definitions in computers do not deter the proliferation of word senses. Instead, computers lead to a rapid increase in the production of new microsenses — to use a word coined by Alan Cruse (2000). In Unix, for example, lines of a file are separated by newline characters; in the Macintosh, however, they are separated by carriage-return characters; in Windows, they are separated by a carriage return followed by a new line; and in IBM mainframes, the operating system keeps track of individual lines, which it returns without any separating characters. Furthermore, these four major types of files are constantly being subdivided into new subtypes with new definitions for every release, update, or patch to every operating system. Similar developments occur in every branch of science and engineering, and even closely related branches have different definitions for the same words and different words with the same definitions.
These difficulties cause the process of interpreting language to resemble puzzle solving: the words that appear in a text and the background knowledge required to interpret the text are like pieces in a jigsaw puzzle that are scrambled in an unpredictable order. Puzzle solving requires constraint satisfaction methods, which assemble pieces of the semantic puzzle to derive an interpretation of the text in terms of some selection of theories in the infinite lattice. With conceptual graphs, the semantic patterns associated with each word sense are represented by canonical conceptual graphs (Sowa 1976, 1992), which serve as the pieces of the semantic puzzle. The structure of the lexicon, as described by Sowa (1984), is illustrated in Figure 6, which shows the relationships of word types, word senses, canonical graphs, and formal theories.
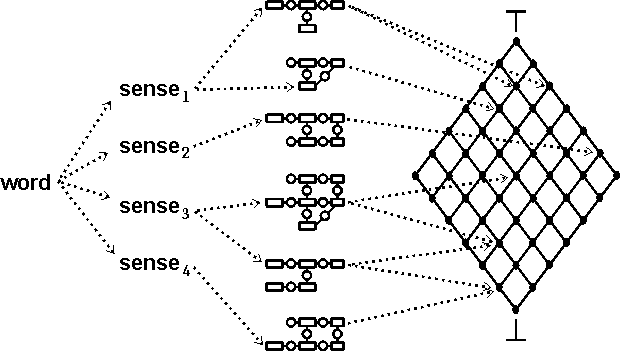
Figure 6: A structured lexicon for mapping words to theories
The dotted arrows in Figure 6 link the word types of any language to an open-ended number of word senses or concept types, each of which is linked to one or more canonical graphs, which are puzzle pieces of possibly different shapes. At the right is a lattice of all possible theories, each of which represents a collection of axioms, theorems, and facts about some domain, which may be some aspect of some real, possible, planned, or hypothetical situation Each canonical graph maps to one or more theories in which its logical pattern is used. Following are the four kinds of entities shown in Figure 6:
The puzzle pieces may be expressed in a logical notation, but the labels on the nodes of a graph or the predicates of a formula cannot be limited to a fixed lexicon or a predefined formal ontology. The labels are signs, whose relations to any world, real or imaginary, must be determined by the semiotic processes. Different theories may use the same labels, but theories on different branches of the lattice may define the labels in incompatible ways.
In his logic of pragmatism, Peirce had solved the so-called symbol-grounding problem about the relationship between the physical world and the symbols used in language and logic (Vogt 2000). Although Peirce maintained that there is no limit to the number of possible levels of interpretation in any semiotic system, he avoided the unconstrained speculation of the deconstructionists by insisting that every symbol be grounded, directly or indirectly, at the two "gates" of perception and action:
The elements of every concept enter into logical thought at the gate of perception and make their exit at the gate of purposive action; and whatever cannot show its passports at both those two gates is to be arrested as unauthorized by reason. (EP 2.241).Peirce's three basic methods of reasoning include induction, abduction and deduction: induction for discovering the elements, abduction for combining and rearranging the elements to form new hypotheses, and deduction for deriving the implications. These processes may be used iteratively. After a hypothesis is formed by abduction, its implications must be tested against reality. If its implications are not confirmed, the hypothesis must be revised in another stage of abduction. The elements can only originate in perception: abduction cannot create new elements, but it can reassemble previously observed elements in novel combinations. Each combination defines a new concept, whose full meaning is determined by the totality of purposive actions it implies. As Peirce said, meanings grow as new information is received, new implications are derived, and new actions become possible.
To illustrate the relationships, Figure 7 shows an agent who repeatedly carries out the stages of induction, abduction, deduction, and action. The arrow of induction indicates the accumulation of patterns that have been useful in previous applications. The crystal at the top symbolizes the elegant, but fragile theories that are constructed from chunks in the knowledge soup by abduction. The arrow above the crystal indicates the process of belief revision, which uses repeated abductions to modify the theories by expansion, contraction, revision, and analogy. At the right is a prediction derived from a theory by deduction. That prediction leads to actions whose observable effects may confirm or refute the theory. Those observations are the basis for new inductions, and the cycle continues.

Figure 7: Peirce's logic of pragmatism
As Figure 7 illustrates, the chunks of knowledge in the soup enter through the gate of perception and are recognized as repeatable patterns by the process of induction. The crystalline theories at the top are hypotheses assembled by abduction. Those theories whose predictions lead to successful actions are added to the soup as chunks that become available for further abductions. The more often a chunk is used, the higher its salience or likelihood for future selections.
Learning is the process of accumulating chunks of knowledge in the soup and organizing them into theories — collections of consistent beliefs that prove their value by making predictions that lead to successful actions. Learning by any agent — human, animal, or robot — involves a constant cycling from data to models to theories and back to a reinterpretation of the old data in terms of new models and theories. Beneath it all, there is a real world, which the entire community of inquirers learns to approximate through repeated cycles of induction, abduction, deduction, and action.
To evaluate the truth of any statement in science or everyday life, Peirce (1909) had developed a version of model-theoretic semantics, but he was not satisfied with a definition of truth as a static correspondence between a sentence and a particular model of the world. Instead, he believed in a potential infinity of mathematical models, which could be applied to various aspects of the world, but he also rejected a relativistic view that all models are equally good. Instead, Peirce defined truth as the ultimate goal of a search through an infinity of models that give better and better approximations to an ever wider range of phenomena. The denotation of a proposition in terms of a particular model must be supplemented by the scientific method of experiment, observation, and test to determine whether the model is an adequate approximation to the world for the purpose at hand. Following are some quotations in which Peirce summarized that view:
Peirce's definition of truth and his logic of pragmatism, which supports that definition, are an elegant generalization of the practices of working scientists. Yet many philosophers who seized upon one brief quotation have failed to appreciate their full ramifications. In a survey of various theories of truth, Kirkham (1992) said
Peirce's theory of truth is plausible only because it is parasitic on another, hidden theory of truth: truth as correspondence with reality. So why doesn't Peirce simply offer the latter as his theory of truth? (p. 83)If Kirkham had read more of Peirce's writings, he might have found the answer to his question:
That truth is the correspondence of a representation with its object is, as Kant says [1787, A58, B82], merely the nominal definition of it. Truth belongs exclusively to propositions. A proposition has a subject (or set of subjects) and a predicate. The subject is a sign; the predicate is a sign; and the proposition is a sign that the predicate is a sign of that of which the subject is a sign. If it be so, it is true. But what does this correspondence, or reference of the sign to its object, consist in? The pragmaticist answers this question as follows... if we can find out the right method of thinking and can follow it out, — the right method of transforming signs, — then truth can be nothing more nor less than the last result to which the following out of this method would ultimately carry us. (EP 2.379-380)
Quine (1960), as usual, is more subtle, but he hadn't read much more of Peirce's writings than Kirkham:
But there is a lot wrong with Peirce's notion, besides its assumption of a final organon of scientific method and its appeal to an infinite process. There is a faulty use of numerical analogy in speaking of a limit of theories, since the notion of limit depends on that of "nearer than," which is defined for numbers and not for theories. And even if we by-pass such troubles by identifying truth somewhat fancifully with the ideal result of applying scientific method outright to the whole future totality of surface irritations, still there is trouble in the imputation of uniqueness ("the ideal result").... It seems likelier, if only on account of symmetries or dualities, that countless alternative theories would be tied for first place. (p. 23)
Quine's objection has three parts, each of which requires a separate answer:
Peirce used the term finite fallibilism to characterize his views about truth and scientific method as a means for discovering truth:
On the whole, then, we cannot in any way reach perfect certitude nor exactitude. We never can be absolutely sure of anything, nor can we with any probability ascertain the exact value of any measure or general ratio....Peirce was not a relativist. He believed that knowledge is possible and that a great deal of what people believe they know is probably true within the limits of perception and measurement used in everyday life. Yet there is no way of knowing whether any particular statement is absolutely true without qualification. In fact, many statements that have been tested to the most exacting standards available today may only be useful approximations that could turn out to be unreliable or counterproductive tomorrow.But it would be quite misunderstanding the doctrine of fallibilism to suppose that it means that twice two is probably not exactly four. As I have already remarked, it is not my purpose to doubt that people can usually count with accuracy. Nor does fallibilism say that men cannot attain a sure knowledge of the creations of their own minds. It neither affirms nor denies that. It only says that people cannot attain absolute certainty concerning questions of fact. (CP 1.147-149)
Copyright ©2005 by John F. Sowa
Last Modified: