
Figure 1. The meaning triangle
Abstract. The Internet is a giant semiotic system. It is a massive collection of Peirce's three kinds of signs: icons, which show the form of something; indices, which point to something; and symbols, which represent something according to some convention. But current proposals for ontologies and metadata have overlooked some of the most important features of signs. A sign has three aspects: it is (1) an entity that represents (2) another entity to (3) an agent. By looking only at the signs themselves, some metadata proposals have lost sight of the entities they represent and the agents — human, animal, or robot — which interpret them. With its three branches of syntax, semantics, and pragmatics, semiotics provides guidelines for organizing and using signs to represent something to someone for some purpose. Besides representation, semiotics also supports methods for translating patterns of signs intended for one purpose to other patterns intended for different but related purposes. This article shows how the fundamental semiotic primitives are represented in semantically equivalent notations for logic, including controlled natural languages and various computer languages.
Presented at ICCS'2000 in Darmstadt, Germany, on August 14, 2000. Published in B. Ganter & G. W. Mineau, eds., Conceptual Structures: Logical, Linguistic, and Computational Issues, Lecture Notes in AI #1867, Springer-Verlag, Berlin, 2000, pp. 55-81.
Ontologies contain categories, lexicons contain word senses, terminologies contain terms, directories contain addresses, catalogs contain part numbers, and databases contain numbers, character strings, and BLOBs (Binary Large OBjects). All these lists, hierarchies, and networks are tightly interconnected collections of signs. But the primary connections are not in the bits and bytes that encode the signs, but in the minds of the people who interpret them. The goal of various metadata proposals is to make those mental connections explicit by tagging the data with more signs. Those metalevel signs themselves have further interconnections, which can be tagged with metametalevel signs. But meaningless data cannot acquire meaning by being tagged with meaningless metadata. The ultimate source of meaning is the physical world and the agents who use signs to represent entities in the world and their intentions concerning them.
The study of signs, called semiotics, was independently developed by the logician and philosopher Charles Sanders Peirce and the linguist Ferdinand de Saussure. The term comes from the Greek sêma (sign); Peirce originally called it semeiotic, and Saussure called it semiology, but semiotics is the most common term today. As Saussure (1916) defined it, semiology is a field that includes all of linguistics as a special case. But Peirce (CP 2.229) had an even broader view of that includes every aspect of language and logic within the three branches of semiotics:
Unfortunately, most word processors deal only with a small subset of syntax. They have produced what St. Laurent (1999) calls the WYSIWYG disaster: "Plain text, dull though it may be, is much easier to manage than the output of the average word processor or desktop publishing program." In practice, the slogan "What you see is what you get" actually means WYSIAYG: "What you see is all you get." The text is so overburdened with formatting tags that there is no room for semantics or pragmatics. The so-called Rich Text Format (RTF) is semantically the most impoverished representation for text ever devised. Formatting is an aspect of signs that makes them look pretty, but it fails to address the more fundamental question of what they mean.
To address meaning, the markup languages in the SGML family were designed with a clean separation between formatting and meaning. When properly used, SGML and its successor XML use tags in the text to represent semantics and put the formatting in more easily manageable style sheets. That separation is important, but the semantic tags themselves must have a clearly defined semantics. Most XML manuals, however, provide no guidelines for representing semantics. Following is an excerpt from one of the proposed standards for representing resources in XML:
A resource can be anything that has identity. Familiar examples include an electronic document, an image, a service (e.g., "today's weather report for Los Angeles"), and a collection of other resources. Not all resources are network "retrievable"; e.g., human beings, corporations, and bound books in a library can also be considered resources. (Berners-Lee, et al. 1998)In that report, an electronic document is considered familiar, but human beings are unfamiliar "resources" mentioned only as an afterthought. Yet without the people, the document and its contents have no meaning.
Many of the ontologies for web objects ignore physical objects, processes, people, and their intentions. A typical example is SHOE (Simple HTML Ontology Extensions), which has only four basic categories: String, Number, Date, and Truth (Heflin et al. 1999). Those four categories, which are needed to describe the syntax of web data, cannot by themselves describe the semantics. Strings contain characters that represent statements that describe the world; numbers count and measure things; dates are time units tied to the rotation of the earth; and truth is a metalanguage term about the correspondence between a statement and the world. Those categories can only be defined in terms of the world, the people in the world, and the languages people use to talk about the world. Without such definitions, the categories are meaningless tags that confer no meaning upon the data they are attached to.
In discussing the Resource Description Framework (RDF), which is based on the XML facilities, Bray (1998) presented a broader view of the kinds of categories that web-based metadata should represent:
It seems unlikely that one PropertyType standing by itself is apt to be very useful. It is expected that these will come in packages; for example, a set of basic bibliographic PropertyTypes like Author, Title, Date, and so on. Then a more elaborate set from OCLC, and a competing one from the Library of Congress. These packages are called Vocabularies; it's easy to imagine PropertyType vocabularies describing books, videos, pizza joints, fine wines, mutual funds, and many other species of Web wildlife.This is a good statement of one issue, but it raises other issues: How are the packages related to one another? How is the Date property of the OCLC package related to the Vintage property of a wine package? Can packages inherit type definitions from other packages? If two packages are competing, is there any way to define conversion rules for translating or redefining the types of one in terms of another? A human reader may know that a wine vintage can be compared to an OCLC date, but without a formal definition, the computer cannot.
Ironically, the computer networks that make it easier to transmit data have made it more difficult to share data. In continuing his discussion, Bray raised further issues:
Nobody thinks that everyone will use the same vocabulary (nor should they), but with RDF we can have a marketplace in vocabularies. Anyone can invent them, advertise them, and sell them. The good (or best-marketed) ones will survive and prosper. Probably, most niches of information will come to be dominated by a small number of vocabularies, the way that library catalogues are today.There are already thousands, if not millions of competing vocabularies. The tables and fields of every database and the lists of items in every product catalog for every business in the world constitute incompatible vocabularies. When product catalogs were distributed on paper, any engineer or contractor could read the catalogs from different vendors and compare the specifications. But minor variations in the terminology of computerized catalogs can make it impossible for a computer system to compare components from different vendors.
By standardizing the notations, XML and RDF take an important first step, but that step is insufficient for data sharing without some way of comparing, relating, and translating the vocabularies. Phipps (2000) warned that standardizing the vocabularies may create even more difficulties "by hiding complexities behind superficial agreements":
To connect from the heart of my e-business to the heart of yours would be impossibly expensive in shared systems without XML, but even with it the system analysis needed to create the translation is a significant task. We should not assume that XML is a panacea or that the standardization of vocabularies will automatically bring interoperability. XML provides us with a medium to express our understanding of the meaning of data, but we still have to discern realities and differences of meanings when we exchange data.More important than standardizing vocabularies is the development of methods for defining and translating vocabularies. To have a sound semantics and pragmatics, those methods must relate the terms in the vocabularies to the things they refer to and to the people who use them to communicate information about those things.
The purpose of this paper is to analyze the differences of meaning, to explore their implications for web-based metadata, and to show how the methods of logic and ontology can be used to define, relate, and translate signs from one vocabulary to another. Among the methods discussed in this paper are Peirce's systems of logic, ontology, and semiotics, which are presented in more detail in the book Knowledge Representation by Sowa (2000).
Metalanguage consists of signs that signify something about other signs, but what they signify depends on what relationships those signs have to each other, to the entities they represent, and to the agents who use those signs to communicate with other agents. Figure 1 shows the basic relationships in a meaning triangle (Ogden and Richards 1923). On the lower left is an icon that resembles a cat named Yojo. On the right is a printed symbol that represents his name. The cloud on the top gives an impression of the neural excitation induced by light rays bouncing off Yojo and his surroundings. That excitation, called a concept, is the mediator that relates the symbol to its object.

Figure 1. The meaning triangle
The triangle in Figure 1 has a long history. Aristotle distinguished objects, the words that refer to them, and the corresponding experiences in the psychê. Frege and Peirce adopted that three-way distinction from Aristotle and used it as the semantic foundation for their systems of logic. Frege's terms for the three vertices of the triangle were Zeichen (sign) for the symbol, Sinn (sense) for the concept, and Bedeutung (reference) for the object. As an example, Frege cited the terms morning star and evening star. Both terms refer to same object, the planet Venus, but their senses are very different: one means a star seen in the morning, and the other means a star seen in the evening. Following is Peirce's definition of sign:
A sign, or representamen, is something which stands to somebody for something in some respect or capacity. It addresses somebody, that is, creates in the mind of that person an equivalent sign, or perhaps a more developed sign. That sign which it creates I call the interpretant of the first sign. The sign stands for something, its object. It stands for that object, not in all respects, but in reference to a sort of idea, which I have sometimes called the ground of the representamen. (CP 2.228)The terms morning star and evening star are distinct signs that create different concepts or interpretants in the mind of the listener. Both concepts stand for the same object, but in respect to a different ground, which depends on the time of the observation.
Aristotle observed that symbols could symbolize other symbols, as "written words are symbols of the spoken." Frege said that his logic could be used as a language to talk about the logic itself. But Peirce went further than either of them in recognizing that multiple triangles could be linked together in different ways by attaching a vertex of one to a vertex of another. By stacking another triangle on top, Figure 2 represents the concept of representing an object by a concept. The upper triangle relates the cloud that suggests the concept of Yojo to the symbol [Cat: Yojo], which is a printable symbol for the more elusive neural excitation. At the very top is a cloud for the neural excitation that occurs when some person recognizes that Yojo is being represented by a printed symbol.

Figure 2. Concept of representing an object by a concept
Meaning triangles can be linked side by side to represent signs of signs of signs. On the left of Figure 3 is the triangle of Figure 1, which relates Yojo to his name. The middle triangle relates the name Yojo to the quoted string "Yojo". The rightmost triangle relates that character string to its encoding as a bit string 0x596F6A6F. In each of the three triangles, the symbol is related to its object by a different metalevel process: naming, quoting, or representing. At the top of each triangle, the clouds that represent the unobservable neural excitations have been replaced by concept nodes that serve as printable symbols of those excitations. The concept node [Cat: Yojo] is linked by the conceptual relation node (Name) to a node for the concept of the name [Word: "Yojo"], which is linked by the conceptual relation node (Repr) to a node for the concept of the character string itself [String: 'Yojo']. The resulting combination of concept and relation nodes is an example of a conceptual graph (CG).

Figure 3. Object, name of object, symbol of name, and character string
To deal with meaning, semiotics must go beyond relationships between signs to the relationships of signs, the world, and the agents who observe and act upon the world. Symbols are highly evolved signs that are related to actual objects by previously established conventions. People agree to those conventions by relating the symbols to more primitive signs, such as icons, which signify their objects by some structural similarity, and indices, which signify their objects by pointing to them. All these signs can be related to one another by linking series or even arrays of triangles. Additional triangles could show how a name is related to the person who assigns the name, to the reason for giving an object one name rather than another, or to an index that points to some location where the object may be found.
Different kinds of applications require different levels of detail in the metadata. For information retrieval (IR), a simple string search can often find a web page with the desired information. To find information about Yojo the cat, it could search for the strings "Yojo" and "cat"; to find information about Queequeg's ebony idol in the novel Moby Dick, it could search for the strings "Yojo" and "Queequeg". IR systems depend on a human reader to decide which strings to search for and to interpret the results that are retrieved. Systems that go beyond simple search must be able to distinguish the physical object Yojo from an icon that resembles the object, the name of the object, and the character string that represents the name. Following is an interchange between a human user who asked a question and a computer system that did not make those distinctions:
Q: What is the largest state in the US? A: Wyoming.To answer questions about sizes, the computer would use the greater-than operator to compare numbers. When it applied that operator to the character strings, it found the last state in alphabetical order, which does not happen to be the largest state in either area or population. A loosely defined system of metadata may be adequate for finding information, but inadequate for any further processing. As Phipps observed, superficial agreements about vocabulary may hide complexities that make interoperability impossible.
The second branch of semiotics is semantics, or as Peirce called it, logic proper — the subject that studies what it means for a pattern of signs to represent a true proposition about the things the signs refer to. The first complete system of first-order logic (FOL) was the Begriffsschrift by Gottlob Frege (1879), who developed a notation that no one else, not even his very few students, ever adopted. The second complete system was the algebraic notation for predicate calculus, independently developed by Charles Sanders Peirce (1883, 1885). With minor modifications, it became the most commonly used version of logic during the twentieth century. It is a much better notation than Frege's Begriffsschrift, but for many people, it is "too mathematical." The third complete system was Peirce's existential graphs of 1897, which he called his chef d'oeuvre — a strong claim by a man who invented the most widely used version of logic today.
With existential graphs, Peirce set out to determine the simplest, most primitive forms for expressing the elements of logic. Although he developed a graphical notation for expressing those forms, they can be expressed equally well in a natural language, an algebraic notation, or many different linear, graphical, or even spoken representations. The following table lists Peirce's five semantic primitives, each illustrated with an English example. Since these five elements are primitive, they cannot be formally defined in terms of anything more primitive; instead, the middle column of the table briefly states their "informal meaning."
| Primitive | Informal Meaning | English Example |
|---|---|---|
| Existence | Something exists. | There is a dog. |
| Coreference | Something is the same as something. | The dog is my pet. |
| Relation | Something is related to something. | The dog has fleas. |
| Conjunction | A and B. | The dog is running, and the dog is barking. |
| Negation | Not A. | The dog is not sleeping. |
The five primitives in Table 1 are available in every natural language and in every version of first-order logic. They are called semantic primitives because they go beyond syntactic relations between signs to semantic relations between signs and the world. Any notation that is capable of expressing these five primitives in all possible combinations must include all of FOL as a subset. As an example, the WHERE clause of the SQL query language can express each of these primitives and combine them in all possible ways; therefore, first-order logic is a subset of SQL. Different languages may use different notations for representing the five primitives:
| Operator | English Example | Translation to Primitives |
|---|---|---|
| Universal | Every dog is barking. | not(there is a dog and not(it is barking)) |
| Implication | If there is a dog, then it is barking. | not(there is a dog and not(it is barking)) |
| Disjunction | A dog is barking, or a cat is eating. | not(not(a dog is barking) and not(a cat is eating)) |
Instead of choosing existence and conjunction as primitives, Frege chose the universal and implication as primitives. Then he defined existence and conjunction in terms of his primitives. The result was not as readable as Peirce's algebraic notation, but it was semantically equivalent. Peirce's existential graphs (EGs) were also semantically equivalent to both of the other notations, but they had the simplest of all mappings to the five primitives. SQL also uses existence, conjunction, and negation as its three basic primitives, but it provides the keyword OR as well. SQL has no universal quantifier, which must be represented by a paraphrase of the form NOT EXISTS... NOT. To add logical operators to RDF, Berners-Lee (1999) proposed the tags <not> and <exists>, which can be combined with the implicit conjunction of RDF to define the operators of Table 2.
To illustrate various notations for logic and their relationships to RDF, consider a typical sentence that might be used in a database specification: Every human being has two distinct parents, who are also human beings. Since this sentence introduces numbers and plurals, which go beyond the five primitives, start with the simpler sentence Some human has a parent, who is also human. Figure 4 shows an existential graph that represents the sentence.

Figure 4. EG for Some human has a parent who is human.
In an existential graph, the words represent predicates or relations, and the bars represent existential quantifiers. The two bars in Figure 4 represent two individuals who are human, and the one on the left has the one on the right as a parent. In the algebraic notation, each bar would be assigned a variable, such as x or y, and an existential quantifier, represented by the symbol ∃. As a result, Figure 4 would map to the following formula:
(∃x)(∃y)(Human(x) ∧ HasParent(x,y) ∧ Human(y)).The symbol ∧ in the formula represents conjunction, which is implicit in the EG and RDF notations. Figure 4 could be represented by a triple in RDF: the first human could be treated as an RDF resource, the HasParent relation as an RDF property type, and the second human as an RDF value. The existence of the human on the left would be indicated by the proposed RDF quantifier <exists var="x">, and the one on the right by <exists var="y">.
The EG in Figure 5 would require an additional relation or property type before it could be represented in RDF. It represents the sentence Some human has one parent who is human, another parent who is human, and the two are not identical.

Figure 5. EG for Some human has two distinct human parents.
The bar that represents (∃x) in Figure 4 is connected to both copies of the HasParent relation in Figure 5. Two bars represent each of the human parents. If they were connected, they would represent the same individual; but to represent distinct individuals, the connection must be negated. In existential graphs, Peirce used an oval to indicate negation; in Figure 5, the oval negates part of the connecting bar. In the algebraic notation, Figure 5 would be represented by the following formula:
(∃x)(∃y)(∃z)
(Human(x) ∧ HasParent(x,y) ∧ Human(y)
∧ HasParent(x,z) ∧ Human(z) ∧ y≠z).
The inequality y≠z
corresponds to the negated connecting bar in Figure 5.
In EGs, the bar that represents a variable also represents coreference,
and its negation represents inequality. Notations that have variables,
such as predicate calculus, SQL, and RDF, must also have a coreference
operator, such as = and its negation ≠. With new property types
for Equal and NotEqual, Figure 5 could be represented in RDF
by three existential quantifiers linked together by three RDF triples.
The small oval in Figure 5 is sufficient to negate the connection between the bar for one parent y and the bar for the other parent z, but an oval can be made as large as necessary to show the scope of negation. To show a universal quantifier, Table 2 shows that two negations are necessary, which are represented by a pair of large ovals in Figure 6. Literally, the resulting graph may be read It is false that there exists a human being who does not have two distinct parents. It corresponds to the following formula:
~(∃x)(Human(x) ∧ ~(∃y)(∃z)
(HasParent(x,y) ∧ Human(y)
∧ HasParent(x,z) ∧ Human(z) ∧ y≠z)).
Two copies of the proposed RDF tag
<not> and its ending tag </not>
could be nested to provide the equivalent of the two nested ovals
in Figure 6. To make RDF equivalent to existential graphs,
however, new RDF rules would be needed to restrict the scope
of the quantified variables to the contexts enclosed by the tags
<not> and </not>.

Figure 6. EG for Every human has two distinct human parents.
As Table 2 illustrates, a pair of negations can represent either a universal quantifier or an implication. The EG in Figure 6 may be read in either way. If the two ovals are considered an implication, Figure 6 could be read If there exists a human, then that human has a parent who is human and another parent who is human and the two parents are distinct. Another option is to read an existential quantifier nested between two ovals as the universal quantifier ∀, which is expressed by the English word every. Then Figure 6 could be read Every human has a parent who is human and another parent who is human and the two parents are distinct. By using the defined operators of Table 2, the formula could be rewritten in a form that shows the universal quantifier ∀ and the implication ⊃ explicitly:
(∀x)(Human(x) ⊃ (∃y)(∃z)
(HasParent(x,y) ∧ Human(y)
∧ HasParent(x,z) ∧ Human(z) ∧ y≠z)).
In English, this formula may be read For every x, if x is human,
then there exist a y and a z such that x has the human y as parent,
x has the human z as parent, and y and z are not the same individual.
With their minimal number of operators, Peirce's EGs have a single canonical form instead of the multiple synonymous sentences in languages with more built-in operators, such as English and predicate calculus. That property, which is sometimes an advantage, can be a disadvantage when the most natural or convenient translation is not obvious. Conceptual graphs (Sowa 1984, 2000) are a graphic notation for logic based on existential graphs, but with extended features that support more direct translations to natural languages. Figure 7 shows a conceptual graph that corresponds to the existential graph in Figure 6.

Figure 7. CG for If there is a human, then he or she has two distinct human parents.
Logically, the CG in Figure 7 is semantically equivalent to the EG in Figure 6. To indicate the intended reading, the CG has two boxes explicitly labeled If and Then instead of the EG ovals. Unlike EGs, which use a bar to represent existential quantification, coreference, and connections between relations, those three functions are distinguished in CGs: boxes, called concept nodes, represent quantification; dotted lines represent coreference; and solid lines represent connections between the concept nodes and the relation nodes. The node T in the Then context, which is coreferent with the node [Human] in the If context, corresponds to a pronoun, such as he, she, or it. Altogether, Figure 7 may be read If there is a human, then he or she has two distinct human parents. To improve the readability of logic expressed in RDF, Berners-Lee also proposed the tags <if> and <then> as synonyms for <not>.
Natural languages have a variety of quantifiers, such as the words every, some, or all, the numbers two, seventeen, or half, and the phrases more than six or at least as many. Those generalized quantifiers can be defined in logic by adding Peano's axioms to define numbers and set theory to define collections, but it is convenient to have such quantifiers built into the notation. In CGs, the default quantifier is the existential ∃, which is normally represented by a blank, but concept nodes may also contain defined quantifiers, such as the symbol ∀ or @every to represent the English word every. The CG in Figure 8 is equivalent to Figure 7 by the definition of the quantifier ∀. It maps to the following formula in typed predicate calculus:
(∀x:Human)(∃y,z:Human) (HasParent(x,y) ∧ HasParent(x,z) ∧ y≠z).In typed logic, monadic predicates such as Human(x) are replaced by type labels associated with the variables. The typed formula is more concise, but logically equivalent to the untyped formulas that represent the EG of Figure 6.

Figure 8. CG for Every human has two distinct human parents.
Figure 8 could be represented in RDF with the proposed <forall> quantifier, but CGs also support other generalized quantifiers that have not yet been considered for RDF. As an example, Figure 9 simplifies Figure 8 by introducing the generic plural symbol {*} to represent a set and the number 2 to represent its count or cardinality. The resulting CG can be mapped to the following formula:
(∀x:Human)(∃s:Set)(∀y∈s) (Count(s,2) ∧ HasParent(x,y) ∧ Human(y)).This formula may be read For every x of type Human, there exists an s of type Set such that for every y in s, the count of s is 2, x has y as parent, and y is human. The generalized quantifier {*}@2 in the CG maps to two quantified variables in predicate calculus: a variable s that ranges over sets and a variable y that ranges over the elements of the set s.

Figure 9. CG for Every human has a set of two human parents.
The CG in Figure 9 is closer to English, but it still isn't quite as simple as the more natural sentence Every human has two parents. That sentence could be expressed directly by the CG in Figure 10.

Figure 10. CG for Every human has two parents.
In English, the HasParent relation is normally expressed by the verb have combined with the noun parent. That noun belongs to a large class of role words, such as spouse, pilot, lawyer, assistant, pet, weed, crop, entrance, obstacle, or facility. Syntactically, those words resemble nouns like man, woman, dog, or tree; but semantically, they imply some relationships to external entities. In the ontology of the book Knowledge Representation (Sowa 2000), the primitive relation Has is used to form dyadic relations by combining with concept types that represent roles. Figure 11 shows how the HasParent relation is defined in terms of the relation Has and the role type Parent.

Figure 11. Definition of the HasParent relation.
Figure 11 defines the HasParent relation as a synonym for a conceptual graph that has two concepts designated as formal parameters: the symbol λ1 marks the first parameter as a human who has a parent that is coreferent with another human, marked as the second parameter by the symbol λ2. It may be read The HasParent relation is defined as a relation between two humans; the first has a parent who is the second. With this definition, Figure 10 can be mapped to or from Figure 9. With appropriate definitions of sets and numbers, Figure 9 can be mapped to or from Figure 8, which can be mapped to or from the existential graph or any of the algebraic formulas in typed or untyped predicate calculus. To support equivalent definitions, RDF would require a tag such as <lambda> or <parm> to mark a formal parameter.
In addition to the semantic primitives of Table 1, Peirce distinguished a context-dependent primitive, which he called an indexical. In natural languages, indexicals are represented by pronouns, by deictic words such as this and that, and by noun phrases marked by the definite article the. In conceptual graphs, indexicals are marked by the # symbol. The concept [Cat], for example, represents some unspecified cat that happens to exist; but the concept [Cat: #] represents the cat that was most recently mentioned in the current context. Peirce observed that proper names are also indexicals. Within the context of this article, the name Yojo may refer to a cat or to Queequeg's ebony idol. On the Internet, it also refers to some Japanese people, to others who have adopted that word as a nickname, and to an organization of young journalists. The ambiguity of names and their context dependencies are major concerns addressed by the naming conventions of the Internet. Those conventions are semiotic features that can be represented by metalevel types and relations in conceptual graphs and other logic-based notations.
In summary, the algebraic notation for logic, which is popular with mathematicians, is only one of an open-ended number of semantically equivalent notations. The five semantic primitives of Table 1 and the mechanisms for defining the other operators of first-order logic can be adapted to a wide variety of notations, including natural languages and the web-oriented notations of XML and RDF.
For better readability, any of the logical notations mentioned in this section can be translated to controlled natural languages. One important application, for example, is the generation of comments and help messages automatically from the implementation. Such translations would guarantee that the comments and help would always be up to date, consistent with the implementation, and immediately available in every supported national language.
Pure logic is ontologically neutral. It makes no presuppositions about what exists or may exist in any domain or any language for talking about the domain. To represent knowledge about a specific domain, it must be supplemented with an ontology that defines the categories of things in that domain and the terms that people use to talk about them. The ontology defines the words of a natural language, the predicates of predicate calculus, the concept and relation types of conceptual graphs, the classes of an object-oriented language, or the tables and fields of a relational database. To illustrate the issues of defining an ontology, consider the conceptual graph in Figure 12, which represents the sentence Yojo is chasing a mouse.

Figure 12. CG for Yojo is chasing a mouse.
Figure 12 uses three concepts and two conceptual relations. The concept [Cat: Yojo] represents a cat named Yojo; [Chase] represents an instance of chasing; and [Mouse] represents a mouse. The conceptual relation (Agnt) indicates that Yojo is the agent of chasing, and (Thme) indicates that the mouse is the theme or the one that is being chased. The CG is logically equivalent to the following formula in typed predicate calculus:
(∃x:Cat)(∃y:Chase)(∃z:Mouse) (name(x,"Yojo") ∧ agnt(y,x) ∧ thme(y,z)).This formula and the CG in Figure 12 introduce several ontological assumptions: there exist entities of types Cat, Chase, and Mouse; some entities have character strings as names; and Chase can be linked to concepts of other entities by relations of type Agent and Theme.
The representation of actions by distinct concepts follows Peirce's ontology, which represents an action such as chasing with three distinct entities: the one that is chasing, the one that is being chased, and the act of chasing itself. The relations (Agnt) and (Thme) are examples of the case relations or thematic roles of linguistics. Instead of Peirce's ontology, which is also called event semantics, some logicians would represent the verb is chasing by a single predicate, such as chases:
(∃x:Cat)(∃y:Mouse) (name(x,"Yojo") ∧ chases(x,y)).The ontology of this formula could also be used in a conceptual graph:
[Cat: Yojo]→(Chases)→[Mouse].This CG, which is written in the linear notation for CGs, can be translated to Figure 12 by defining the relation (Chases) in terms of the concept [Chase]:
Chases ::= [Animate: λ1]←(Agnt)←[Chase]→(Thme)→[MobileEntity: λ2].With this definition of (Chases), the ontology of the previous CG can be translated to or from the ontology assumed in Figure 12.
Although the Chases relation allows shorter graphs and formulas than the concept [Chase], it introduces other complexities into the ontology. A general representation for tenses and modality, for example, would require a proliferation of relation types, such as HasChased, WillChase, and MustHaveBeenChasing. Furthermore, the dyadic relation chases(x,y) makes no provision for attaching adverbs and other modifiers to the verb. Figure 13 takes advantage of the more general representation to define the concept type Chase in terms of a graph for an animate agent (parameter #1) that is following a mobile entity (parameter #2) in a rapid manner.

Figure 13. Definition of the concept type Chase
Figure 13 is only a partial definition because it represents a necessary, but not a sufficient condition. Runners in a race, for example, might be following one another rapidly, but only because they are pursuing a common goal. A more complete definition must include the purpose, which might be different for different senses of the word chase. Figure 14 defines one sense, called ChaseHunt, in which the purpose of the agent is to catch the mobile entity that is being chased.

Figure 14. Definition of the concept type ChaseHunt
In Figure 14, the purpose relation (Purp) links the action to a situation that would occur upon the successful completion of the chase. According to Peirce, purpose is a triadic relation, of which two arguments are shown explicitly in Figure 14. The implicit third argument is the agent of Chase, whose intention is to bring about the desired situation. That situation is nested inside a context box because its intentional status is different from the context of the act of chasing. If the chase is unsuccessful, the act of catching might never occur. Figure 15 defines another concept type ChaseAway, in which the agent's purpose is not to catch the mobile entity, but to cause it to leave its current location.

Figure 15. Definition of the concept type ChaseAway
The ontology of situations and their representation in contexts is based on Peirce's logic combined with ideas developed in artificial intelligence, linguistics, philosophy, and logic over the past 40 years (Sowa 2000). A context box may enclose modal or intentional situations, as in Figures 14 and 15, or it may enclose temporally or spatially separated parts of a larger situation. In Figure 16, the large situation with its sequence of nested situations represents the following passage in English:
At 10:17 UTC, there was a situation involving a cat named Yojo and a mouse. Yojo chased the mouse. Then he caught the mouse. Then he ate the head of the mouse.These sentences show how indexicals are used to make context-dependent references. When new entities are first mentioned, they are introduced with the indefinite article, as in the phrases a situation, a cat named Yojo, and a mouse. The two middle sentences refer to the mouse with the definite article the and to the cat with the name Yojo or the pronoun he. In the last sentence, the head of the mouse, which had not been mentioned explicitly, is marked with the definite article because the introduction of the mouse implicitly introduces all of its expected parts. In Figure 16, the indexicals are marked with the # symbol: the pronoun he is represented as #he, and the definite article the is represented with the # symbol by itself.

Figure 16. Nested situations with unresolved indexicals
The large context box of Figure 16 encloses the entire situation, which occurred at the point in time (PTim) of 10:17 UCT. It contains concept nodes that represent the cat Yojo, the mouse, and three nested situations connected by the (Next) relation. Before that CG can be translated to predicate calculus, the indexicals must be resolved to links or labels that explicitly show the coreferences. To avoid multiple line crossings, Figure 17 introduces the coreference labels *x for Yojo and *y for the mouse. Subsequent references use the same labels, but with the prefix ? in the bound occcurrences of [?x] for Yojo and [?y] for the mouse. The # symbol in the concept [Head: #] of Figure 16 is erased in Figure 17, since the head of a normal mouse is uniquely determined when the mouse itself is identified.

Figure 17. Nested situations with indexicals resolved
After the indexicals have been resolved to coreference labels, Figure 17 can be translated to the following formula in typed predicate calculus:
(∃s1:Situation)(pTim(s1,"10:17 UTC")
∧ dscr(s1,
(∃s1,s2,s3:Situation)(∃x:Cat)(∃y:Mouse)(name(x,"Yojo")
∧ dscr(s2, (∃u:Chase)(agnt(u,x) ∧ thme(u,y)))
∧ dscr(s3, (∃v:Catch)(agnt(v,x) ∧ thme(v,y)))
∧ dscr(s4,
(∃w:Eat)(∃z:Head)(agnt(w,x) ∧ ptnt(w,z) ∧ part(y,w)))
∧ next(s2,s3) ∧ next(s3,s4)))).
The description predicate dscr(s,p), which
corresponds to the context boxes of Figure 16, is a metalevel relation
between a situation s and a proposition p that describes
s. Figure 17 or its translation to predicate calculus could also
be paraphrased in a version of controlled English that uses variables
to show coreference explicitly: At 10:17 UTC, there was a situation s
involving a cat x named Yojo and a mouse y. In the situation s,
x chased y; then x caught y; then x ate the head of y.
The contexts of conceptual graphs are based on Peirce's logic of existential graphs and his theory of indexicals. Yet the CG contexts happen to be isomorphic to the similarly nested discourse representation structures (DRS), which Hans Kamp (1981a,b) developed for representing and resolving indexicals in natural languages. When Kamp published his first version of DRS, he was not aware of Peirce's graphs. When Sowa (1984) published his book on conceptual graphs, he was not aware of Kamp's work. Yet the independently developed theories converged on semantically equivalent representations; therefore, Sowa and Way (1986) were able to apply Kamp's techniques to conceptual graphs. Such convergence is common in science; Peirce and Frege, for example, started from very different assumptions and converged on equivalent semantics for FOL, which 120 years later is still the most widely used version of logic. Independently developed, but convergent theories that stand the test of time are a more reliable basis for standards than the consensus of a committee.
Since all combinations of the five primitives of Table 1 can be expressed in every natural language, it is possible to represent first-order logic in a subset of any natural language. Such a subset, called a stylized or controlled NL, can be read by anyone who can read the unrestricted NL. As examples, the English paraphrases of the CGs and formulas in this article represent a version of controlled English. With an appropriate selection of syntax rules, that subset could be formalized as a representation of FOL that would be semantically equivalent to any of the common notations for logic.
For most people, no training is needed to read a controlled NL, but some training is needed to write it. For computers, it is easy to translate a controlled NL to or from logic, but fully automated understanding of unrestricted NL is still an unsolved research problem. To provide semiautomated tools for analyzing unrestricted language, Doug Skuce (1995, 1998, 2000) has designed an evolving series of knowledge extraction (KE) systems, which he called CODE, IKARUS, and DocKMan (Document-based Knowledge Management). The KE tools use a version of controlled English called ClearTalk, which is intelligible to both people and computers. As input, the KE tools take documents written in unrestricted NL, but they require assistance from a human editor to generate ClearTalk as output. Once the ClearTalk has been edited and approved, further processing by the KE tools is fully automated. The ClearTalk statements can either be stored in a knowledge base or be written as annotations to the original documents. Because of the way they're generated, the comments that people read are guaranteed to be logically equivalent to the computer implementation.
The oldest logic patterns expressed in controlled natural language are the four types of statements used in Aristotle's system of syllogisms. Each syllogistic rule combines a major premise and a minor premise to draw a conclusion. Following are examples of the four sentence patterns:
Other important logic patterns are the if-then rules used in expert systems. In some rule-based systems, the controlled language is about as English-like as COBOL, but others are much more natural. Attempto Controlled English (Fuchs et al. 1998; Schwitter 1998) is an example of a rich, but unambiguous language that uses a version of Kamp's theory for resolving indexicals. Following are two ACE rules used to specify operating procedures for a library database:
If a copy of a book is checked out to a borrower and a staff member returns the copy then the copy is available.
If a staff member adds a copy of a book to the library
and no catalog entry of the book exists
then the staff member creates a catalog entry
that contains the author name of the book
and the title of the book
and the subject area of the book
and the staff member enters the id of the copy
and the copy is available.
Rules like these are translated automatically to the
Horn-clause subset of FOL, which is the basis for Prolog
and many expert system languages. The subset of FOL consisting
of Horn-clause rules plus Aristotelian syllogisms can be executed
efficiently, but it is powerful enough to specify a Turing machine.
For database queries and constraints, natural language statements with the full expressive power of FOL can be translated to SQL. Although many NL query systems have been developed, none of them have yet become commercially successful. The major stumbling block is the amount of effort required to define the vocabulary terms and map them to appropriate fields of the database. But if KE tools are used to design the database, the vocabulary needed for the query system can be generated as a by-product of the design process. As an example, the RÉCIT system (Rassinoux 1994; Rassinoux et al. 1998) uses KE tools to extract knowledge from medical documents written in English, French, or German and translates the results to a language-independent representation in conceptual graphs. The knowledge extraction process defines the appropriate vocabulary, specifies the database design, and adds new information to the database. The vocabulary generated by the KE process is sufficient for end users to ask questions and get answers in any of the three languages.
Design and specification languages have multiple metalevels. As an example, the Unified Modeling Language has four levels: the metametalanguage defines the syntax and semantics of the UML notations; the metalanguage defines the general-purpose UML types; a systems analyst defines application types as instances of the UML types; finally, the working data of an application program consists of instances of the application types. To provide a unified view of all these levels, Olivier Gerbé and his colleagues at the DMR Consulting Group implemented design tools that use conceptual graphs as the representation language at every level (Gerbé et al. 1995, 1996, 1997, 1998, 2000). For his PhD dissertation, Gerbé developed an ontology for using CGs as the metametalanguage for defining CGs themselves. He also applied it to other notations, including UML and the Common KADS system for designing expert systems. Using that theory, Gerbé and his colleagues developed the Method Repository System for defining, editing, and displaying the methods used by the DMR consultants. Internally, the knowledge base is stored in conceptual graphs, but externally, the graphs can be translated to web pages in either English or French. About 200 business processes have been modeled in a total of 80,000 CGs. Since DMR is a Canadian company, the language-independent nature of CGs is important because it allows the specifications to be stored in the neutral CG form. Then any manager, systems analyst, or programmer can read them in his or her native language.
Translating an informal diagram to a formal notation of any kind is as difficult as translating unrestricted NL to executable programs. But it is much easier to translate a formal representation in any version of logic to controlled natural languages, to various kinds of graphics, and to executable specifications. Walling Cyre and his students have developed KE tools for mapping both the text and the diagrams from patent applications and similar documents to conceptual graphs (Cyre et al. 1994, 1997, 1999). Then they implemented a scripting language for translating the CGs to circuit diagrams, block diagrams, and other graphic depictions. Their tools can also translate CGs to VHDL, a hardware design language used to specify very high speed integrated circuits (VHSIC).
No single system discussed in this paper incorporates all the features desired in a KE system, but the critical research has been done, and the remaining work requires more development effort than pure research. Figure 18 shows the flow of information from documents to logic and then to documents or to various computational representations. The dotted arrow from documents to controlled languages requires human assistance. The solid arrows represent fully automated translations that have been implemented in one or more systems.
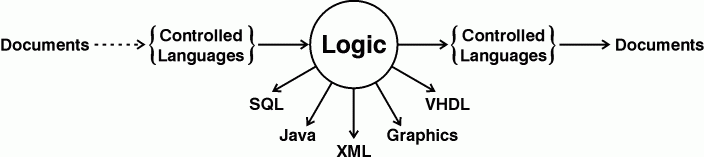
Figure 18. Flow of information from documents to computer representations
For the KE tools, the unifying representation language is logic, which may be implemented in different subsets and notations for different tools. All the subsets, however, use the same vocabulary of natural-language terms, which map to the same ontology of concepts and relations. From the user's point of view, a KE system communicates in a subset of natural language, and the differences between tools appear to be task-related differences rather than differences in language.
Berners-Lee, Tim, R. Fielding, & L. Masinter, eds. (1998) Uniform Resource Identifiers (URI): Generic Syntax, Internet RFC 2396.
Berners-Lee, Tim (1999) The Semantic Toolbox: Building Semantics on top of XML-RDF, http://www.w3.org/DesignIssues/Toolbox.html.
Bray, Tim (1998) "RDF and Metadata," http://www.xml.com/xml/pub/98/06/rdf.html.
Bray, Tim, Dave Hollander, & Andrew Layman, eds. (1999) Namespaces in XML, W3 TR REC-xml-names.
Cyre, W. R., S. Balachandar, & A. Thakar (1994) "Knowledge visualization from conceptual structures," in Tepfenhart et al. (1994) Conceptual Structures: Current Practice, Lecture Notes in AI 835, Springer-Verlag, Berlin, pp. 275-292.
Cyre, W. R. (1997) "Capture, integration, and analysis of digital system requirements with conceptual graphs," IEEE Trans. Knowledge and Data Engineering, 9:1, 8-23.
Cyre, W. R., J. Hess, A. Gunawan, & R. Sojitra (1999) "A Rapid Modeling Tool for Virtual Prototypes ," in 1999 Workshop on Rapid System Prototyping, Clearwater, FL.
Frege, Gottlob (1879) Begriffsschrift, English translation in J. van Heijenoort, ed. (1967) From Frege to Gödel, Harvard University Press, Cambridge, MA, pp. 1-82.
Fuchs, Norbert E., Uta Schwertel, Rolf Schwitter (1998) "Attempto Controlled English — not just another logic specification language," Proceedings LOPSTR'98, Manchester.
Fuchs, Norbert E., Uta Schwertel, Rolf Schwitter (1999) Attempto Controlled English (ACE), Language Manual, Version 3.0, Technical Report ifi-99.03, University of Zurich.
Genesereth, Michael R., & Richard Fikes, eds. (1998) Knowledge Interchange Format (KIF), draft proposed American National Standard, NCITS.T2/98-004.
Gerbé, Olivier, & M. Perron (1995) "Presentation definition language using conceptual graphs," in G. Ellis, R. A. Levinson, & W. Rich, eds., Conceptual Structures: Applications, Implementation, and Theory, Lecture Notes in AI 954, Springer-Verlag, Berlin.
Gerbé, Olivier, B. Guay, & M. Perron (1996) "Using conceptual graphs for methods modeling," in P. W. Eklund, G. Ellis, & G. Mann, eds., Conceptual Structures: Knowledge Representation as Interlingua, Lecture Notes in AI 1115, Springer-Verlag, Berlin, pp. 161-174.
Gerbé, Olivier (1997) "Conceptual graphs for corporate knowledge management," in D. Lukose, H. Delugach, M. Keeler, L. Searle, & J. Sowa, eds., Conceptual Structures: Fulfilling Peirce's Dream, Lecture Notes in AI 1257, Springer-Verlag, Berlin, pp. 474-488.
Gerbé, Olivier, R. Keller, & G. Mineau (1998) "Conceptual graphs for representing business processes in corporate memories," in M-L Mugnier & Michel Chein, eds., Conceptual Structures: Theory, Tools, and Applications, Lecture Notes in AI 1453, Springer-Verlag, Berlin, pp. 401-415.
Gerbé, Olivier, & Brigitte Kerhervé (1998) "Modeling and metamodeling requirements for knowledge management," in Proc. of OOPSLA'98 Workshops, Vancouver.
Gerbé, Olivier (2000) Un Modèle uniforme pour la Modélisation et la Métamodélisation d'une Mémoire d'Entreprise, PhD Dissertation, Département d'informatique et de recherche opérationelle, Université de Montréal.
Heflin, Jeff, James Hendler, & Sean Luke (1999) SHOE: A Knowledge Representation Language for Internet Applications, Technical Report CS-TR-4078 (UMIACS TR-99-71), Dept. of Computer Science, University of Maryland at College Park.
Kamp, Hans (1981a) "Events, discourse representations, and temporal references," Langages 64, 39-64.
Kamp, Hans (1981b) "A theory of truth and semantic representation," in Formal Methods in the Study of Language, ed. by J. A. G. Groenendijk, T. M. V. Janssen, & M. B. J. Stokhof, Mathematical Centre Tracts, Amsterdam, 277-322.
Kamp, Hans, & Uwe Reyle (1993) From Discourse to Logic, Kluwer, Dordrecht.
Lassila, Ora, & Ralph R. Swick, eds. (1999) Resource Description Framework (RDF) Model and Syntax Specification, http://www.w3.org/TR/REC-rdf-syntax.
Ogden, C. K., & I. A. Richards (1923) The Meaning of Meaning, Harcourt, Brace, and World, New York, 8th edition 1946.
Peirce, Charles Sanders (1885) "On the algebra of logic," American Journal of Mathematics 7, 180-202.
Peirce, Charles Sanders (CP) Collected Papers of C. S. Peirce ed. by C. Hartshorne, P. Weiss, & A. Burks, 8 vols., Harvard University Press, Cambridge, MA, 1931-1958.
Phipps, Simon (2000) "Meaning, not Markup," XML Journal, vol. 1, no. 1, p. 66.
Rassinoux, Anne-Marie (1994) Extraction et Représentation de la Connaissance tirée de Textes Médicaux, Éditions Systèmes et Information, Geneva.
Rassinoux, Anne-Marie, Robert H. Baud, Christian Lovis, Judith C. Wagner, Jean-Raoul Scherrer (1998) "Tuning up conceptual graph representation for multilingual natural language processing in medicine," in M-L Mugnier & M. Chein, eds. (1998) Conceptual Structures: Theory, Tools, and Applications, Lecture Notes in AI 1453, Springer-Verlag, Berlin, pp. 390-397
St. Laurent, Simon (1999) XML: A Primer, second edition, M & T Books, Foster City, CA.
Saussure, Ferdinand de (1916) Cours de Linguistique Générale, translated by W. Baskin as Course in General Linguistics, Philosophical Library, New York, 1959.
Schwitter, Rolf (1998) Kontrolliertes Englisch fúr Anforderungsspezifikationen, Studentdruckerei, Zurich.
Skuce, Doug, & Timothy Lethbridge (1995) "CODE4: A unified system for managing conceptual knowledge," International J. of Human-Computer Studies, 42 413-451.
Skuce, Doug (1998) "Intelligent knowledge management: integrating documents, knowledge bases, and linguistic knowledge," in Proceedings of KAW'98, Calgary.
Skuce, Doug (2000) "Integrating web-based documents, shared knowledge bases, and information retrieval for user help," Computational Intelligence 16:1.
Sowa, John F. (1984) Conceptual Structures: Information Processing in Mind and Machine, Addison-Wesley, Reading, MA.
Sowa, John F., ed. (1998) Conceptual Graphs, draft proposed American National Standard, NCITS.T2/98-003.
Sowa, John F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole, Pacific Grove, CA.
Sowa, John F., & Eileen C. Way (1986) "Implementing a semantic interpreter using conceptual graphs," IBM Journal of Research and Development 30:1, pp. 57-69.
Copyright 2000, John F. Sowa
Last Modified: