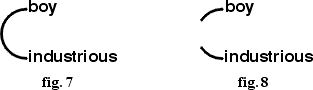On the Algebra of Logic
Comments on Peirce's Paper of 1885
by John F. Sowa
For more background on the history of logic and Peirce's contributions,
see the articles by Putnam (1982),
Quine (1995),
Dipert (1995),
and Hintikka (1997).
Click on any of the dates highlighted in blue to see
the full reference.
1. Historical Background
George Boole (1847,
1854)
applied his algebra to propositions, sets, and
monadic predicates. The expression p×q, for example,
could represent the conjunction of two propositions, the intersection
of two sets, or the conjunction of two monadic predicates.
With his algebra of dyadic relations,
Peirce (1870) made the first
major breakthrough in extending symbolic logic to predicates
with two arguments (or subjects, as he called them).
With that notation, he could represent expressions such as
"lovers of women with bright green complexions".
That version of the relational algebra was developed further
by Ted Codd (1970, 1971),
who earned his PhD
under Arthur Burks, the editor of volumes 7 and 8 of Peirce's
Collected Papers.
At IBM, Codd promoted relational algebra as the foundation
for database systems, a version of which was adopted
for the query language SQL, which is used in all relational database
systems today. Like Peirce's version of 1870, Codd's relational algebra
and the SQL language leave the existential quantifier implicit
and require a double negation to express universal quantification.
From 1880
to 1885,
Peirce developed his general algebra of relations,
which Giuseppe Peano (1889)
adopted as the basis for the modern notation of predicate calculus.
Gottlob Frege (1879) had developed
an equivalent notation for logic, which he called
the Begriffsschrift (concept writing), but no one else
ever used it.
The modern notation for predicate calculus is based on Peirce's notation,
which in turn was an extension of Boolean algebra. Like Boole,
Peirce adopted mathematical symbols to represent logical operators.
Since Peano wanted to use logic to represent mathematics,
he replaced Peirce's symbols with new symbols that could be
freely mixed with mathematical symbols in the same formulas.
To form the logical symbols, Peano began the practice
of turning letters upside down or backwards.
The following table lists Peirce's symbols and Peano's replacements:
|
Peirce's Notation |
Peano's Notation |
| Operation
| Symbol
| Explanation
| Symbol
| Explanation
|
| Disjunction |
+ |
Logical sum |
∨ |
v for vel |
| Conjunction |
× |
Logical product |
∧ |
Upside down v |
| Negation |
− |
−1=0 and −0=1 |
~ |
Curly minus sign |
| Implication |
−< |
Equal or less than |
⊃ |
C for consequentia |
| Existential Quantifier |
Σ |
Iterated sum |
∃ |
E for existere |
| Universal Quantifier |
Π |
Iterated product |
( ) |
O for omnis |
|
For his logical algebra, Boole used 1 for truth and 0 for falsehood,
and he chose the symbols +, ×, and
− to represent
disjunction, conjunction, and negation.
The bottom three lines of the table are Peirce's innovations:
- Implication: Peirce observed that if p implies q,
then q must always be true when p is true, but q
might also be true for some reason independent of p.
Therefore, the truth value of p is always less than or equal
to the truth value of q. Instead of using the symbol ≤,
which combines two operators, Peirce invented the claw symbol
−< because it suggests a single indivisible operation.
- Existential quantifier: In Boolean algebra, 1+1=1. Therefore,
Peirce adopted Σ to indicate a logical summation of any number
of terms, which would be true if at least one of the terms happened
to be true.
- Universal quantifier: He aslo adopted Π to indicate
a logical product of any number of terms, which would only be true
if every one of the terms happened to be true.
In 1880, Peirce began to use the symbols Π and Σ, which he
called quantifiers, shortly after
Frege (1879) had independently
developed his Begriffsschrift (concept writing).
A few years later,
Peirce (1885) published complete rules of inference
for first-order logic by adding the rules for quantifiers
to the usual rules for Boolean algebra. For the next 30 years,
Frege's work was largely ignored.
In Germany, Ernst Schröder (1890-95)
adopted Peirce's notation,
which was used for most work on logic for over 20 years.
In Italy, the logicians followed Peano,
who declared Frege's notation to be unreadable.
In England, Bertrand Russell praised Frege, but adopted the Peirce-Peano
notation, which came to be called Peano-Russell notation.
Quantifiers
Model Theory
In the next paragraph,
Peirce mentions endoporeutic, which is his "outside-in" method
of determining the truth value of an existential graph.
Endoporeutic is logically equivalent to
model theory,
which Alfred Tarski (1935, 1936)
developed many years later. As Peirce said, logic is
"the formal science of the conditions of the truth
of representations" (CP 2.229); model theory and endoporeutic
are two logically equivalent methods for defining those conditions.
Before Peirce, the most detailed development of the model-theoretic
approach was by William of Ockham. To see the similarity,
compare the following quotations from Ockham, Peirce, and Tarski:
- Ockham (1323) showed how to
determine the truth value of compound propositions in terms of the
truth or falsity of their components and to determine the validity
of rules of inference (regulae generales consequentiarum)
in terms of the truth of their antecendents and consequents.
Following are three quotations from Part II and two from Part III
of the Summa Logicae, which Peirce had studied in detail:
- "We must posit certain rules which are common to the signs
'every', 'any', 'each', and others like them, if there are any others.
These rules are also common to many propositions which are equivalent
to hypothetical propositions, e.g. 'Every man is an animal', 'Every
white thing is running', etc.... It should be noted that for the truth
of such a universal proposition it is not required that the subject and
the predicate be in reality the same thing. Rather, it is required
that the predicate supposit for all those things that the subject
supposits for, so that it is truly predicated of them."
- "A conjunctive proposition is one which is composed of two
or more categoricals joined by the conjunction 'and' or by some particle
equivalent to such a conjunction. For example, this is a conjunctive
proposition: 'Socrates is running and Plato is debating'.... Now
for the truth of a conjunctive proposition, it is required that both
parts be true. Therefore, if any part of a conjunctive proposition
is false, then the conjunctive proposition itself is false."
- "A disjunctive proposition is one which is composed of two
or more categoricals joined by the disjunction 'or' or by some
equivalent. For example, this is a disjunctive proposition: 'You are
a man or a donkey.' Likewise, this is a disjunctive proposition:
'You are a man or Socrates is debating.' Now for the truth of a
disjunctive proposition, it is required that some part be true....
It should be noted that the contradictory opposite of a disjunctive
proposition is a conjunctive proposition composed of the contradictories
of the parts of the disjunctive proposition." [Note that this
is Ockham's version of DeMorgan's law that the negation of
p∨q is (~p)∧(~q)].
- "From truth, falsity never follows. Therefore, when the
antecedent is true and the consequent is false, the inference
is not valid."
- "From a false proposition, a true proposition may follow.
Hence this inference does not hold: 'The antecedent is false; therefore,
the consequent is false.' But the following inference holds: 'The
consequent is false; therefore, so is the antecedent.'"
- Peirce (1869):
"All that the formal logician has to say is, that if
facts capable of expression in such and such forms of words are true,
another fact whose expression is related in a certain way to the
expression of these others is also true.... The proposition 'If A,
then B' may conveniently be regarded as equivalent to 'Every case
of the truth of A is a case of the truth of B.'".
- Tarski (1936): "In terms of these
concepts [of model], we can define the concept of logical consequence
as follows: The sentence X follows logically from the sentences
of the class K if and only if every model of the class K is also
a model of the class X."
Tarski's advance over Ockham consists in defining the truth
of a formula in terms of his formal notion of model.
But Peirce made an equivalent advance by defining
the truth of an EG by his formal method of endoporeutic.
The rule of interpretation which
necessarily follows from the diagrammatization is that the interpretation is
"endoporeutic" (or proceeds inwardly) that is to say a ligature denotes
"something" or "anything not" according as its outermost part
lies on an unshaded or a shaded area respectively.
Although Peirce's endoporeutic is logically equivalent to Tarski's
model theory, the proof of equivalence was not discovered until
Hintikka (1973, 1985) developed
game-theoretical semantics
as a simpler, more elegant method than Tarski's.
Then Hilpinen (1982)
showed that Peirce's endoporeutic is equivalent
to the techniques of game-theoretical semantics.
Sowa (1984)
adopted game-theoretical semantics to define the model
theory for conceptual graphs,
which are based on Peirce's EGs. For their introductory textbook,
Barwise and Etchemendy (1993) adopted
game-theoretical semantics as a simplified method for teaching
model theory.
In modern terminology, endoporeutic can be defined
as a two-person zero-sum
perfect-information game, of the same genre as board games
like chess, checkers, and tic-tac-toe. Unlike those games,
which frequently end in a draw, every finite EG determines a game
that must end in a win for one of the two players in a finite
number of moves. For a typical formula in logic, the complexity
of the game is closer to tic-tac-toe than to chess, but in principle
the game can be played with an EG of any size. In fact, the first
logician to develop the technique of game-theoretical semantics
was Leon Henkin (1959), who showed
that it could sometimes be used to evaluate the denotation
of infinitely long formulas in a finite number of steps.
In the game of endoporeutic, one player, called the proposer,
tries to show that a given EG is true, and another player,
called the skeptic, tries to show that it is false.
The game begins with an EG whose truth value is to be determined and
a Tarski-style model M=(D,R),
in which D is a set of individuals and R is a collection
of relations defined over D.
For convenience, the model M can also be represented as an EG in which
there are no negations, each individual in D is represented by a line
of identity, and each tuple in R is represented by a copy
of the character string that names the corresponding relation (see the
method of representing relations
by graphs).
If the EG to be evaluated contains no negations, it would be true
if the proposer could find any mapping (graph homomorphism) of the lines
of identity and relations of the EG to the lines of identity and
relations of the model M.
Such a mapping, which embodies Peirce's notion of "diagrammatic,"
formalizes the correspondence theory of truth.
If no such mapping exists, the EG would be false.
The correspondence theory of truth runs into difficulties when the
proposition to be evaluated contains negations or any operator
that is defined in terms of negation — that includes
disjunction, implication, and the universal quantifier. With
endoporeutic, Peirce invented a method of peeling off negations
one at a time until there are none left. If an EG to be evaluated
contains negations, the two players in the game of endoporeutic
must remove them according to the following rules:
- If the current EG is empty (a blank sheet of assertion),
the current proposer wins, and the current skeptic loses.
- If the current EG consists of just a single negation (shaded oval),
the negation is removed by unshading the outermost oval and reversing
the shading of any nested areas. Then the two players switch sides:
the current proposer becomes the new skeptic, and the current skeptic
becomes the new proposer.
- If the current EG consists of two or more negations (shaded ovals
with no graph components outside an oval), the current skeptic chooses
any one of the ovals as the current EG, and all the other ovals are erased.
- If the current EG contains a subgraph g outside of any
shaded area, the current proposer tries to find a mapping (graph
homomorphism) of g into the model graph M.
There are two possibilities:
- If no such mapping can be found, the current proposer loses,
and the current skeptic wins.
- If one or more such mappings are possible, the proposer has
the option of selecting any one. The inverse of that mapping determines
an assignment of some individual in D to each line of identity
in g.
After the proposer has made the selection, any lines of identity that
extend from g into any ovals that occur in the current EG can
never be reassigned to any other individuals in D. Then the graph
g is erased, leaving either a blank sheet of assertion
or a sheet containing one or more shaded ovals.
Since each of these rules reduces the size of the EG, any game
that starts with a finite EG must end in a finite number of moves.
Since none of the stopping conditions results in a draw,
either the original proposer or the original skeptic must have
a winning strategy for any given EG and model M.
If the proposer has a winning strategy, the EG is true
in terms of M; otherwise, it is false in terms of M.
This definition of endoporeutic is based on Peirce's writings, but
the wording of the statement takes advantage of many concepts that
were developed in mathematics and computer science during the twentieth
century: recursive definitions, graph homomorphisms, game theory,
and the game-playing algorithms of artificial intelligence.
Peirce had written many pages about endoporeutic, but no one clearly
deciphered them until Hilpinen noticed the similarity to the
game-theoretical approach.
Only after mathematicians had caught up to Peirce did they have
the concepts and vocabulary for interpreting what he was trying to say.
There are three simple rules for modifying premises when they have once
been scribed in order to get any sound necessary conclusion from them.
Of course I do not count among these rules two recommendations
which are nevertheless of the highest importance. One is to be sure to
scribe every premise that is really pertinent to the conclusion one aims
at. The other is to scribe them with sufficient analysis of their meaning,
and not by any means to neglect abstractions which modern philosophers
think most foolishly are of little or no importance or are even unreal
because they are of the nature of signs. They tell us that it is
we who create the law of nature! That is Real which is true just
the same whether you or any collection of persons opine
or otherwise think it true or not.
The planets were always accelerated toward the sun for
millions of years before any finite mind was in being to have any opinion
on the subject; therefore the law of gravitation is a Reality.
In the following digression, Peirce expresses doubts about the absolute
truth of Newtonian mechanics. All such doubts were summarily dismissed
by Simon Newcomb, who had been Peirce's superior at the U.S. Coast
and Geodetic Survey, but they were vindicated by Einstein's
theory of relativity. The discrepancy in the orbit of Mercury,
in fact, was part of the evidence used to confirm the general theory
of relativity (Einstein 1916, 1921).
As early as 1891, Peirce had suspected that the geometry of the universe
was non-Euclidean, and he requested funding (which Newcomb denied)
for astronomical observations to test whether the sum of the angles
of a triangle is exactly 180°. That suspicion was finally
confirmed during an eclipse of the sun in 1919, when a measurement
of the deflection of a light ray was consistent with Einstein's predicted
value for the curvature of space caused by the mass of the sun.
I do not say that Newton's formulation of the
law of gravitation is quite right, because when Newcomb was at work on
the inferior planets, Mercury and Venus, I wrote to him and called his
attention to the fact that certain motions of Mercury go to show that the
attraction is not precisely inversely as the 2nd power of the distance
but is rather proportional to the 2.01 power or thereabouts; I see that
in his tables not only of Mercury but also of Venus he has introduced
such a correction. He says he introduces it to make his tables accord
with observation. He does not say that the cause of the discrepancy
of observation with Newton's law. But that is the way I can see
[to think of or] account for it.
I had not supposed it will be prescriptible in so circular an orbit as
that of Venus. No doubt all our new formulations of laws are merely
approximate; but the laws, as they really are, are Real.
The distinction between nominalism and realism is a theme that Peirce
discussed reapeatedly:
Anybody may happen to opine that "the" is a real English word; but
that will not constitute him a realist. But if he thinks that, whether
the word "hard" itself be real or not, the property, character,
the predicate, hardness is not invented by men, as the word is,
but is really and truly in the hard things and is one in them all,
as a description of habit, disposition, or behaviour, then
he is a realist. (CP 1.27n1)
In logic, Peirce combined Boole's symbolic approach with the work
of the medieval logicians, of which Ockham was one of the greatest.
In metaphysics, however, Peirce disagreed with Ockham's nominalism
and preferred the realism of Ockham's predecessor, John Duns Scotus.
But Peirce also added some important qualifications:
In calling himself a Scotist, the writer does not mean that he is going
back to the general views of 600 years back; he merely means that
the point of metaphysics upon which Scotus chiefly insisted and which
has passed out of mind, is a very important point, inseparably bound up
with the most important point to be insisted upon today.
(CP 4.50)
In terms of Peirce's categories, the nominalists were masters
of Firstness and Secondness, and the important point they ignored
was Thirdness, which is central to the reality of physical laws.
Yet Peirce always emphasized the equal status of all three categories.
In distinguishing his triads from Hegel's, Peirce rejected the idea
that "Firstness and Secondness must somehow
be aufgehoben" (CP 5.91).
I will now state what modifications are permissible
in any graph we may have scribed.
Peirce's three permissions correspond to what Ockham called
regulae consequentiarum or rules of inference.
In another passage (CP 4.423), Peirce
called them "formal "rules"... by which
one graph may be transformed into another without danger of passing
from truth to falsity and without referring to any interpretation
of the graphs." Each permission may be viewed as a pair of rules,
one of which states conditions for inserting a graph,
and the other states conditions for erasing a graph.
In this commentary, the insertion rules are numbered 1i, 2i, 3i;
the erasure rules are 1e, 2e, 3e.
In various discussions, Peirce showed that his rules are sound.
His proof by the method of endoporeutic is equivalent to Tarski's
proof of soundness by model theory.
As Peirce said, there is no "danger of passing
from truth to falsity". It is, however, possible to pass
from falsity to truth. Rule 1e, for example, allows any graph,
true or false, to be erased. Erasing a true graph cannot make
a true statement false, but erasing a false graph may make
a false statement true. For more detailed discussions of Peirce's rules
and proofs of their soundness and completeness,
see Roberts (1973)
or Sowa (1984).
Peirce's rules, in fact, are a generalization and simplification
of the rules for natural deduction, which
Gerhard Gentzen (1935)
independently discovered many years later. Like Peirce's rules,
Gentzen's rules also come in pairs, one of which inserts an operator,
which the other removes. Unlike Peirce's rules,
Gentzen's rules are more numerous and more complex because they were
designed for the more complex algebraic notation (which Peirce discarded
in favor of EGs precisely because the graphs have a simpler structure).
For both Peirce and Gentzen, the only axiom is a blank sheet of paper:
anything that can be proved without any prior assumptions is a theorem.
1st Permission. Any graph-instance on an
unshaded area may be erased; and on a shaded area that already exists,
any graph-instance may be inserted. This includes the right to cut any
line of identity on an unshaded area, and to prolong one or join two on
a shaded area. (The shading itself must not be erased of course, because
it is not a graph-instance.)
The proof of soundness depends on the fact that erasing graphs by Rule 1e
reduces the number of conditions that might be false, and inserting graphs
by Rule 1i increases the number of conditions that might be false.
Rule 1e, which permits erasures in an unshaded (positive) area,
cannot make a true statement false; therefore, that area must be at least
as true as it was before. Conversely, Rule 1i, which permits insertions
in a shaded (negative), area cannot make a false statement true;
therefore, the negation of that false area must be at least as true
as it was before. For a more formal proof, see
Sowa (1984).
These rules apply equally well to propositional logic and predicate logic.
Since EGs have no variables, the rules for dealing with variables
in the algebraic notation are replaced by simpler rules for cutting
or connecting lines of identity (which corresponds to erasing
or inserting instances of the graph —is—).
In terms of Peirce's endoporeutic, cutting a line allows either end
to be assigned independently to different individuals in a model.
Therefore, cutting a line has the effect
of existential generalization because it allows the two ends
to be assigned to different existentially quantified variables.
The option of connecting two lines in a shaded area has the effect
of universal instantiation, because it allows a universally
quantified variable to be replaced by an arbitrary term.
2nd Permission. Any graph-instance may
be iterated (i.e. duplicated) in the same area or in any area enclosed
within that, provided the new lines of identity so introduced have identically
the same connexions they had before the iteration. And if any graph-instance
is already duplicated in the same area or in two areas one of which is
included (whether immediately or not) within the other, their connexions
being identical, then the inner of the instances (or either of them if
they are in the same area) may be erased. This is called the Rule of Iteration
and Deiteration.
Peirce showed that the rules of iteration (2i) and deiteration (2e)
can never change the truth value of a graph. By endoporeutic, the truth
value of each graph or subgraph is determined at the point when the
outside-in evaluation reaches it. If a subgraph g has the value
true at that point, no copies of g can affect the truth value
of the current area or any enclosed area. If g has the value
false, the current area must already be false, and no copies of g
in the current area or any enclosed area can make the current area true.
In other writings, Peirce gave more detail about how these rules
may be applied to lines of identity as well as to whole graphs.
By iteration (2i), any line of identity may be extended in the same area
or into any enclosed area. By deiteration (2e), any end of a line of
identity that is not attached to another line or to some relation name
may be erased, starting from the innermost area in which it occurs.
Iteration extends a line from the outside inward, and deiteration
retracts a line from the inside outward.
3rd Permission. Any ring-shaped area which is entirely vacant
may be suppressed by extending the areas within and without it
so that they form one. And a vacant ring shaped area may be created
in any area by shading or by obliterating shading so as to separate two
parts of any area by the new ring shaped area.
A vacant ring-shaped area corresponds to a double negation;
i.e., two negation signs ~~ with nothing between them.
The third permission says that a double negation may be drawn around (3i)
or erased around (3e) any graph on any area, shaded or unshaded.
In the game of endoporeutic, a double negation causes the two players
to switch sides twice; therefore, its presence or absence can have no
effect on the final result.
An important qualification, which Peirce discusses elsewhere, is that
such a ring is considered vacant even if it contains lines of identity,
provided that the lines begin outside the ring and continue
to the area enclosed by the ring without having any connections
to one another or to anything else in the area of the ring.
The opening phrase of the next sentence, "It is
evident that", is an exaggeration, since Peirce elsewhere used
many pages to prove that so-called evident conclusion.
It is evident that neither of these [p.19] three principles
will ever permit one to assert more than he has already asserted. I will
give examples the consideration of which will suffice to convince you of
this.
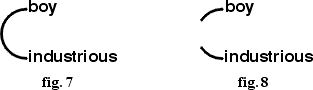
Fig. 7 asserts that some boy is industrious. By the 1st permission it
can be changed to fig. 8, which asserts that there is a boy and that
there is an industrious person. This was asserted as fig. 7, together
with the identity of some case.
Figure 7 may be translated to the following formula:
(∃x)(boy(x) ∧ industrious(x))
This formula is equivalent to the following, which results from
treating the line of identity as if it contained the dyad
—is—, which corresponds to the equality
x=y.
(∃x)(∃y)(boy(x) ∧ industrious(y) ∧ x=y)
Rule 1e, which allows any graph to be erased in a positive area,
has the effect of erasing a dyad —is— to transform
Figure 7 into Figure 8. In the algebraic notation, that rule has
the effect of erasing the equality to produce the formula that
corresponds to Figure 8:
(∃x)(∃y)(boy(x) ∧ industrious(y))
This formula and the graph in Figure 8 assert that there exists a boy
x and something industrious y, and it leaves open the
question of whether the boy and the industrious thing are the same
or different.
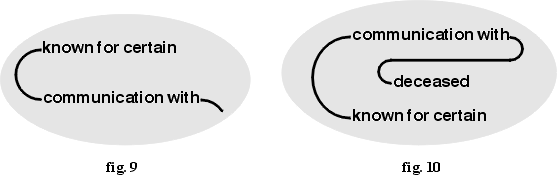
Fig. 9 asserts either there is nothing known for certain or else there
is no communication with anybody. By the same permission this can be
changed to fig. 10 which asserts that no communication with anybody
deceased is known for certain. But this is fully included in the state
of things asserted in fig. 9.
Figure 9 corresponds to the following formula:
~(∃x)(∃y)(knownForCertain(x) ∧ communicationWith(x,y))
This formula may be read "It is false that some x is known for
certain that is a communication with some y." The disjunctive
reading corresponds to the following formula:
(∀x)(∀y)(~knownForCertain(x) ∨ ~communicationWith(x,y))
Literally, this formula may be read "For every x and y, either x is not
known for certain, or there is no communication x with y." By Rule 1i,
the graph —deceased may be inserted in the shaded area.
By a second application of Rule 1i, the unattached end of that graph
may be connected to the unattached end of the graph —communicationWith—
to derive Figure 10, which corresonds to the following formula:
~(∃x)(∃y)(knownForCertain(x) ∧ communicationWith(x,y) ∧ deceased(y)).
This formula may be read "It is false that some x is known for
certain that is a communication with some y who is deceased."
In illustrating the applications of the Second Permission,
I am obliged to notice one of the faults of the system of logic which
has been taught to every generation of young men for some sixty odd
generations. One of the syllogisms that they have all been taught
as a sound apodictic argument called Darapti (and whose validity
nobody has questioned) furnishes a fair sample of the quality of intellect
of the Doctors and Regents of the most famous and proudest Universities.
Here is a sample of it:
Any Phoenix would be a bird
Any Phoenix rises from her own ashes
∴ Some bird rises from its own ashes
In this digression, Peirce comments on a questionable feature
of Aristotle's system of syllogisms: the implicit assumption that
every category has at least one member.
With that assumption, the syllogism Darapti would be sound.
Without that assumption, Peirce's counterexample shows that Darapti
is unsound because a category, such as Phoenix, which has no members
would lead from true premises to a false conclusion.
Peirce used this example to show the need for analyzing rules
of inference in painstaking detail and for justifying each of them
by a method such as his endoporeutic or Tarski's equivalent system
of model theory.
[p.20]They might try to crawl out
of this absurdity by saying that they do not state the premises as
Any Phoenix there may be is a bird
Any Phoenix there may be rises from its ashes
but
Every Phoenix there is is a bird,
etc.
But the reply to that (passing over the fact that Sir Wm Hamilton,
lauded as the highest of authorities, insists that Any
and not Every is the right word) is that by "Contradictories" they mean
two propositions which, by their very meaning, can neither both be true
nor both be false, and they all agree that every simple proposition has
a simple contradictory, and that the contradictory of "Some S is not P"
is "Any, all, or every (Greek pantos) S is P". Now if this latter
implied the existence of some S, Every S is P and Some S is not P could
both be false by there not existing any S. That would be a much graver
fault with their logic than that which I charge against it. For I only
charge that two "moods" or species of syllogism are false. (i.e. not
nessesary, as they profess to be.) And curiously Aristotle never mentions
these with examples as he does in all other cases; but merely says —
But this letter will be long enough without discussing Aristotle and
his commentary, a subject on which I should own [?]
time you,
interesting as it is to me.
In the following paragraph, Peirce states his main argument
for existential graphs: they allow the reasoning steps to be dissected
"into the greatest number of distinct steps",
every one of which is justified by a proof of soundness in terms of
endoporeutic. With his rules of inference and their proof of soundness,
Peirce attained a level of formality and rigor that surpassed anything
achieved by Frege or Russell. Although Frege has been praised for
the meticulous formalization of his proof procedures, he merely
assumed his axioms without proving their truth, and he stated
his rules of inference without proving their soundness. As an example,
Frege's first axiom, written in Peirce-Peano notation, is
a ⊃ (b ⊃ a).
To justify it, Frege (1879)
gives an informal argument: This axiom "says 'The case in which
a is denied, b is affirmed, and a is affirmed
is excluded.' This is evident, since a cannot at the same time
be denied and affirmed." Yet many steps are required to transform
that axiom into the natural language sentence that is supposed
to be "evidently" equivalent. In terms of Peirce's rules, Frege's axiom
can be proved in five steps starting with a blank sheet of paper:

Rule 3i inserts a double negation around the empty graph; another
application of Rule 3i inserts another double negation around
the previous one; Rule 1i inserts a into the shaded area;
Rule 2i iterates a into the innermost area; finally, Rule 1i
inserts b into the other shaded area. The theorem to be proved
contains five symbols, and each step of the proof inserts
one symbol into its proper place in the final result.
Frege had eight other axioms, each of which can be proved by Peirce's
rules in a similarly short proof.
Frege also had two rules of inference, each of which can be proved as
a derived rule of inference from Peirce's rules. Following
is the proof of modus ponens, which starts with an arbitrary
statement p and an implication of the form p⊃q:

Rule 2e deiterates the copy of p in the shaded area;
Rule 1e erases the original copy of p, which is no longer needed;
finally, Rule 3e erases the double negation
to leave the conclusion q by itself.
Frege's other rule of inference is universal generalization,
which allows any term t to be substituted for a universally
quantified variable in a statement of the form
(∀x)P(x). In EGs, the term t would be
represented by a graph of the form —t, which states that
something satisfying the condition t exists, and the universal
quantifier corresponds to a line of identity whose outermost part
occurs in a shaded area:

In the first step, rule 2i iterates (extends) the line of identity
attached to t into the shaded area; Rule 1i inserts a connection
between the two lines in the shaded ara; finally, Rule 3e erases the
double negation. Not only does Peirce "dissect"
the reasoning process into the simplest possible steps, he uses the
method of endoporeutic to ensure that each step is sound.
So I will break off that and just give an illustration
or two of how this Syntax of Existential Graphs works. But before doing
that I wish to draw your attention, in the most emphatic way possible,
to the purpose this Syntax is intended to subserve: since anybody who
did not pay attention to that statement would be all but sure, not merely
to mis[p.21]take the intention of this syntax, but to think that intention
as contrary to what is as well he could. Namely he would suppose the object
was to reach the conclusion from given premises with the utmost facility
and speed, while the real purpose is to dissect the reasoning into the
greatest possible number of distinct steps and so to force attention to
every requisite of the reasoning. The supposed purpose would be
of little consequence, and it is the fussiness of the mathematicians to
furnish inventions to attain it; but the real purpose is to supply a real
and crying need, although logicians are so stupid as not to recognize it
and to put obstacles in the way of meeting it.
Although Peirce does not name the "stupid
logicians" he is criticizing, one of them is probably
Bertrand Russell, whose Principles of Mathematics he reviewed
in 1903:
This is not the place to speak of Mr. Russell's book, which can hardly
be called literature. That he should continue these most severe and
scholastic labors for so long, bespeaks a grit and industry, as well as
a high intelligence, for which more than one of his ancestors have been
famed. Whoever wishes a convenient introduction to the remarkable
researches into the logic of mathematics that have been made during
the last sixty years, and that have thrown a new light both upon
mathematics and upon logic, will do well to take up this book.
But he will not find it easy reading. Indeed, the matter of the second
volume will probably consist, at least nine-tenths of it,
of rows of symbols.
In this lukewarm review, the best that Peirce could say is that
the book is "a convenient introduction."
Since Russell admitted in the preface that he had learned symbolic logic
from Peano at a conference in 1900, he had little to say in 1903
that could impress the man who had invented most of it.
As Putnam (1982) pointed out,
the major developments in logic from 1890 to 1910 were written in
Peirce-Schröder notation, including Zermelo's axioms for set theory,
the Löwenheim-Skolem theorem, and Hilbert's work on the foundations
of mathematics. In a letter to Lady Welby in 1904, Peirce expressed
his opinion more candidly: "Russell's book is
superficial to the point of nauseating me."
The later book, which Peirce correctly predicted would
"probably consist, at least nine-tenths of it,
of rows of symbols" was the Principia Mathematica
by Whitehead and Russell. Although it was an excellent compendium,
the German and Polish logicians found little in it that was new.
Tarski reportedly said that it was "a step backwards."
In the following example, Peirce shows that the syllogism named Barbara
can be proved as a derived rule of inference from his rules for EGs.
In an early article "On the grounds of the validity of the laws of logic,"
Peirce (1869) gave the following
argument for it:
Now, what the formal logician means by an expression of the form,
"Every M is P," is that anything of which M is predicable is P;
thus, if S is M, that S is P. The premise that "Every M is P"
may, therefore, be denied; but to admit it, unambiguously, in the sense
intended, is to admit that the inference is good that S is P if S is M.
There are two points to note about this example: First, Peirce in 1869
was already using model-theoretic arguments in terms of the truth of
"anything of which M is predicable," while
Frege's arguments were nothing but paraphrases in natural language.
Second, Peirce's use of EGs for deriving the rules of inference
of other systems of logic was more formal in 1909 than any argument
that Whitehead and Russell gave in 1910
or even 1925.
References
All bibliographical references have been moved to the
combined bibliography for this web site.