Figure 1: Comparison of logical and analogical reasoning
VivoMind LLC
Abstract. Logical and analogical reasoning are sometimes viewed as mutually exclusive alternatives, but formal logic is actually a highly constrained and stylized method of using analogies. Before any subject can be formalized to the stage where logic can be applied to it, analogies must be used to derive an abstract representation from a mass of irrelevant detail. After the formalization is complete, every logical step — of deduction, induction, or abduction — involves the application of some version of analogy. This paper analyzes the relationships between logical and analogical reasoning and describes a highly efficient analogy engine that uses conceptual graphs as the knowledge representation. The same operations used to process analogies can be combined with Peirce's rules of inference to support an inference engine. Those operations, called the canonical formation rules for conceptual graphs, are widely used in CG systems for language understanding and scene recognition as well as analogy finding and theorem proving. The same algorithms used to optimize analogy finding can be used to speed up all the methods of reasoning based on the canonical formation rules.
This paper was published in the proceedings of the International Conference on Conceptual Structures in Dresden, Germany, in July 2003: A. Aldo, W. Lex, & B. Ganter, eds. (2003) Conceptual Structures for Knowledge Creation and Communication, LNAI 2746, Springer-Verlag, pp. 16-36.
Before discussing the use of analogy in reasoning, it is important to analyze the concept of analogy and its relationship to other cognitive processes. General-purpose dictionaries are usually a good starting point for conceptual analysis, but they seldom go into sufficient depth to resolve subtle distinctions. A typical dictionary lists synonyms for the word analogy, such as similarity, resemblance, and correspondence. Then it adds more specialized word senses, such as a similarity in some respects of things that are otherwise dissimilar, a comparison that determines the degree of similarity, or an inference based on resemblance or correspondence. In AI, analogy-finding programs have been written since the 1960s, but they often use definitions of analogy that are specialized to a particular application.
The VivoMind Analogy Engine (VAE), which is described in Section 3, is general enough to be used in any application domain. Therefore, VAE leads to fundamental questions about the nature of analogy that have been debated in the literature of cognitive science. One three-party debate has addressed many of those issues:
This paper discusses the interrelationships between logical and analogical reasoning, analyzes the underlying cognitive processes in terms of Peirce's semiotics and his classification of reasoning, and shows how those processes are supported by VAE. The same graph operations that support analogical reasoning can also be used to support formal reasoning. Instead of being mutually exclusive, logical reasoning is just a more cultivated variety of analogical reasoning. For many purposes, especially in language understanding, the analogical processes provide greater flexibility than the more constrained and less adaptable variety used in logic. But since logical and analogical reasoning share a common basis, they can be effectively used in combination.
In developing formal logic, Aristotle took Greek mathematics as his model. Like his predecessors Socrates and Plato, Aristotle was impressed with the rigor and precision of geometrical proofs. His goal was to formalize and generalize those proof procedures and apply them to philosophy, science, and all other branches of knowledge. Yet not all subjects are equally amenable to formalization. Greek mathematics achieved its greatest successes in astronomy, where Ptolemy's calculations remained the standard of precision for centuries. But other subjects, such as medicine and law, depend more on deep experience than on brilliant mathematical calculations. Significantly, two of the most penetrating criticisms of logic were written by the physician Sextus Empiricus in the second century AD and by the legal scholar Ibn Taymiyya in the fourteenth century.
Sextus Empiricus, as his nickname suggests, was an empiricist. By profession, he was a physician; philosophically, he was an adherent of the school known as the Skeptics. Sextus maintained that all knowledge must come from experience. As an example, he cited the following syllogism:
Every human is an animal.Sextus admitted that this syllogism represents a valid inference pattern, but he questioned the source of evidence for the major premise Every human is an animal. A universal proposition that purports to cover every instance of some category must be derived by induction from particulars. If the induction is incomplete, then the universal proposition is not certain, and there might be some human who is not an animal. But if the induction is complete, then the particular instance Socrates must have been examimed already, and the syllogism is redundant or circular. Since every one of Aristotle's valid forms of syllogisms contains at least one universal affirmative or universal negative premise, the same criticisms apply to all of them: the conclusion must be either uncertain or circular.
Socrates is human.
Therefore, Socrates is an animal.
The Aristotelians answered Sextus by claiming that universal propositions may be true by definition: since the type Human is defined as rational animal, the essence of human includes animal; therefore, no instance of human that was not an animal could exist. This line of defense was attacked by the Islamic jurist and legal scholar Taqi al-Din Ibn Taymiyya. Like Sextus, Ibn Taymiyya agreed that the form of a syllogism is valid, but he did not accept Aristotle's distinction between essence and accident (Hallaq 1993). According to Aristotle, the essence of human includes both rational and animal. Other attributes, such as laughing or being a featherless biped, might be unique to humans, but they are accidental attributes that could be different without changing the essence. Ibn Taymiyya, however, maintained that the distinction between essence and accident was arbitrary. Human might just as well be defined as laughing animal, with rational as an accidental attribute.
Denouncing logic would be pointless if no other method of reasoning were possible. But Ibn Taymiyya had an alternative: the legal practice of reasoning by cases and analogy. In Islamic law, a new case is assimilated to one or more previous cases that serve as precedents. The mechanism of assimilation is analogy, but the analogy must be guided by a cause that is common to the new case as well as the earlier cases. If the same cause is present in all the cases, then the earlier judgment can be transferred to the new case. As an example, it is written in the Koran that grape wine is prohibited, but nothing is said about date wine. The judgment for date wine would be derived in four steps:
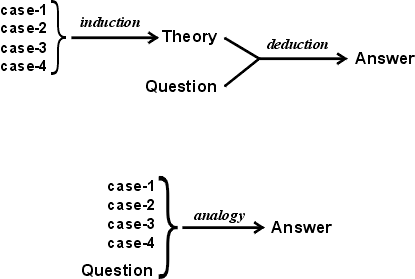
Besides arguing in favor of analogy, Ibn Taymiyya also replied to the logicians who claimed that syllogistic reasoning is certain, but analogy is merely probable. He admitted that logical deduction is certain when applied to purely mental constructions in mathematics. But in any reasoning about the real world, universal propositions can only be derived by induction, and induction must be guided by the same principles of evidence and relevance used in analogy. Figure 1 illustrates Ibn Taymiyya's argument: Deduction proceeds from a theory containing universal propositions. But those propositions must have earlier been derived by induction using the methods of analogy. The only difference is that induction produces a theory as intermediate result, which is then used in a subsequent process of deduction. By using analogy directly, legal reasoning dispenses with the intermediate theory and goes straight from cases to conclusion. If the theory and the analogy are based on the same evidence, they must lead to the same conclusions.

Figure 1: Comparison of logical and analogical reasoning
The question in Figure 1 represents some known aspects of a new case, which has unknown aspects to be determined. In deduction, the known aspects are compared (by a version of structure mapping called unification) with the premises of some implication. Then the unknown aspects, which answer the question, are derived from the conclusion of the implication. In analogy, the known aspects of the new case are compared with the corresponding aspects of the older cases. The case that gives the best match may be assumed as the best source of evidence for estimating the unknown aspects of the new case. The other cases show alternative possibilities for those unknown aspects; the closer the agreement among the alternatives, the stronger the evidence for the conclusion.
Both Sextus Empiricus and Ibn Taymiyya admitted that logical reasoning is valid, but they doubted the source of evidence for universal propositions about the real world. What they overlooked was the pragmatic value of a good theory: a small group of scientists can derive a theory by induction, and anyone else can apply it without redoing the exhaustive analysis of cases. The two-step process of induction followed by deduction has proved to be most successful in the physical sciences, which include physics, chemistry, molecular biology, and the engineering practices they support. The one-step process of case-based reasoning, however, is more successful in fields outside the so-called "hard" sciences, such as business, law, medicine, and psychology. Even in the "soft" sciences, which are rife with exceptions, a theory that is successful most of the time can still be useful. Many cases in law or medicine can be settled by the direct application of some general principle, and only the exceptions require an appeal to a long history of cases. And even in physics, the hardest of the hard sciences, the theories may be well established, but the question of which theory to apply to a given problem usually requires an application of analogy. In both science and daily life, there is no sharp dichotomy between subjects amenable to strict logic and those that require analogical reasoning.
The informal arguments illustrated in Figure 1 are supported by an analysis of the algorithms used for logical reasoning. Following is Peirce's classification of the three kinds of logical reasoning and the way that the structure-mapping operations of analogy are used in each of them:
The VivoMind Analogy Engine (VAE), which was developed by Majumdar, is a high-performance analogy finder that uses conceptual graphs for the knowledge representation. Like SME, structure mapping is used to find analogies. Unlike SME, the VAE algorithms can find analogies in time proportional to (N log N), where N is the number of nodes in the current knowledge base or context. SME, however, requires time proportional to N3 (Forbus et al. 1995). A later version called MAC/FAC reduced the time by using a search engine to extract the most likely data before using SME to find analogies (Forbus et al. 2002). With its greater speed, VAE can find analogies in the entire WordNet knowledge base in just a few seconds, even though WordNet contains over 105 nodes. For that size, one second with an (N log N) algorithm would correspond to 30 years with an N3 algorithm.
VAE can process CGs from any source: natural languages, programming languages, and any kind of information that can be represented in graphs, such as organic molecules or electric-power grids. In an application to distributed interacting agents, VAE processes both English messages and signals from sensors that monitor the environment. To determine an agent's actions, VAE searches for analogies to what humans did in response to similar patterns of messages and signals. To find analogies, VAE uses three methods of comparison, which can be used separately or in combination:
| Analogy of Cat to Car | |
|---|---|
| Cat | Car |
| head | hood |
| eye | headlight |
| cornea | glass plate |
| mouth | fuel cap |
| stomach | fuel tank |
| bowel | combustion chamber |
| anus | exhaust pipe |
| skeleton | chassis |
| heart | engine |
| paw | wheel |
| fur | paint |
As Figure 2 illustrates, there is an enormous amount of background knowledge stored in lexical resources such as WordNet. It is not organized in a form that is precise enough for deduction, but it is adequate for the more primitive method of analogy.
Since there are many possible paths through all the definitions and examples of WordNet, most comparisons generate multiple analogies. To evaluate the evidence for any particular mapping, a weight of evidence is computed by using heuristics that estimate the closeness of the match. For Method #1 of matching type labels, the closest match results from identical labels. If the labels are not identical, the weight of evidence decreases with the distance between the labels in the type hierarchy:
The analogy shown in Figure 2 received a high weight of evidence because VAE found many matching labels and large matching subgraphs in corresponding parts of a cat and parts of a car:
As the cat-car comparison illustrates, analogy is a versatile method for using informal, unstructured background knowledge. But analogies are also valuable for comparing the highly formalized knowledge of one axiomatized theory to another. In the process of theory revision, Niels Bohr used an analogy between gravitational force and electrical force to derive a theory of the hydrogen atom as analogous to the earth revolving around the sun. Method #3 of analogy, which finds matching transformations, can also be used to determine the precise mappings required for transforming one theory or representation into another. As an example, Figure 3 shows a physical structure that could be represented by many different data structures.

Figure 3: A physical structure to be represented by data
Programmers who use different tools, databases, or programming languages often use different, but analogous representations for the same kinds of information. LISP programmers, for example, prefer to use lists, while FORTRAN programmers prefer vectors. Conceptual graphs are a highly general representation, which can represent any kind of data stored in a digital computer, but the types of concepts and relations usually reflect the choices made by the original programmer, which in turn reflect the options available in the original programming tools. Figure 4 shows a representation for Figure 3 that illustrates the typical choices used with relational databases.

Figure 4: Two structures represented in a relational database
On the left of Figure 4 are two structures: a copy of Figure 3 and an arch constructed from three blocks. On the right are two tables: the one labeled Objects lists the identifiers of all the objects in both tables with their shapes and colors; the one labeled Supports lists each object that supports (labeled Supporter) and the object supported (labeled Supportee). As Figure 4 illustrates, a relational database typically scatters the information about a single object or structure of objects into multiple tables. For the structure of pyramids and blocks, each object is listed once in the Objects table, and one or more times in either or both columns of the Supports table. Furthermore, information about the two disconnected structures shown on the left is intermixed in both tables. When all the information about the structure at the top left is extracted from both tables of Figure 4, it can be mapped to the conceptual graph of Figure 5.

Figure 5: A CG derived from the relational DB
In Figure 5, each row of the table labeled Objects is represented by a conceptual relation labeled Objects, and each row of the table labeled Supports is represented by a conceptual relation labeled Supports. The type labels of the concepts are mostly derived from the labels on the columns of the two tables in Figure 4. The only exception is the label Entity, which is used instead of ID. The reason for that exception is that ID is a metalevel term about the representation language; it is not a term that is derived from the entities in the domain of discourse. The concept [Entity: E], for example, says that E is an instance of type Entity. The concept [ID: "E"], however, would say that the character string "E" is an instance of type ID. The use of the label Entity instead of ID avoids mixing the metalevel with the object level. Such mixing of levels is common in most programs, since the computer ignores any meaning that might be associated with the labels. In logic, however, the fine distinctions are important, and CGs mark them consistently.
When natural languages are translated to CGs, the distinctions must be enforced by the semantic interpreter. Figure 6 shows a CG that represents the English sentence, A red pyramid A, a green pyramid B, and a yellow pyramid C support a blue block D, which supports an orange pyramid E. The conceptual relations labeled Thme and Inst represent the case relations theme and instrument. The relations labeled Attr represent the attribute relation between a concept of some entity and a concept of some attribute of that entity. The type labels of concepts are usually derived from nouns, verbs, adjectives, and adverbs in English.
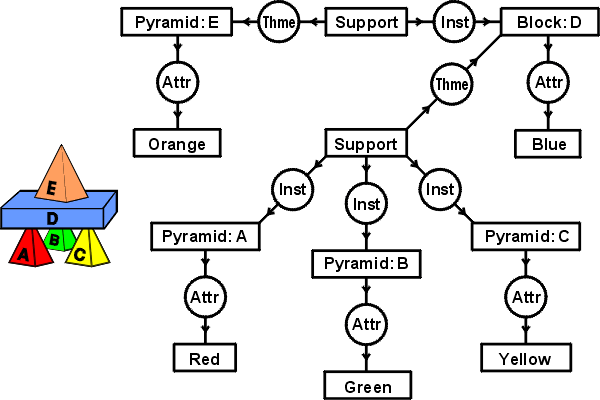
Figure 6: A CG derived from an English sentence
Although the two conceptual graphs represent equivalent information, they look very different. In Figure 5, the CG derived from the relational database has 15 concept nodes and 9 relation nodes. In Figure 6, the CG derived from English has 12 concept nodes and 11 relation nodes. Furthermore, no type label on any node in Figure 5 is identical to any type label on any node in Figure 6. Even though some character strings are similar, their positions in the graphs cause them to be treated as distinct. In Figure 5, orange is the name of an instance of type Color; and in Figure 6, Orange is the label of a concept type. In Figure 5, Supports is the label of a relation type; and in Figure 6, Support is not only the label of a concept type, it also lacks the final S.
Because of these differences, the strict method of unification cannot show that the graphs are identical or even related. Even the more relaxed methods of matching labels or matching subgraphs are unable to show that the two graphs are analogous. Method #3 of analogy, however, can find matching transformations that can translate Figure 5 into Figure 6 or vice-versa. When VAE was asked to compare those two graphs, it found the two transformations shown in Figure 7. Each transformation determines a mapping between a type of subgraph in Figure 5 and another type of subgraph in Figure 6.

Figure 7: Two transformations discovered by VAE
The two transformations shown in Figure 7 define a version of graph grammar for parsing one kind of graph and mapping it to the other. The transformation at the top of Figure 7 can be applied to the five subgraphs containing the relations of type Objects in Figure 5 and relate them to the five subgraphs containing the relations of type Attr in Figure 6. That same transformation could be applied in reverse to relate the five subgraphs of Figure 6 to the five subgraphs of Figure 5. The transformation at the bottom of Figure 7 could be applied from right to left in order to map Figure 6 to Figure 5. When applied in that direction, it would map three different subgraphs, which happen to contain three common nodes: the subgraph extending from [Pyramid: A] to [Block: D]; the one from [Pyramid: B] to [Block: D]; and the one from [Pyramid: C] to [Block: D]. When applied in the reverse direction, it would map three subgraphs of Figure 5 that contained only one common node.
The transformations shown in Figure 7 have a high weight of evidence because they are used repeatedly in exactly the same way. A single transformation of one subgraph to another subgraph with no matching labels would not contribute anything to the weight of evidence. But if the same transformation is applied twice, then its likelihood is greatly increased. Transformations that can be applied three times or five times to relate all the nodes of one graph to all the nodes of another graph have a likelihood that comes close to being a certainty.
Of the three methods of analogy used in VAE, the first two — matching labels and matching subgraphs — are also used in SME. Method #3 of matching transformations, which only VAE is capable of performing, is more complex because it depends on analogies of analogies. Unlike the first two methods, which VAE can perform in (N log N) time, Method #3 takes polynomial time, and it can only be applied to much smaller amounts of data. In practice, Method #3 is usually applied to small parts of an analogy in which most of the mapping is done by the first two methods and only a small residue of unmatched nodes remains to be mapped. In such cases, the number N is small, and the mapping can be done quickly. Even for mapping Figure 5 (with N=9) to Figure 6 (with N=11), the Method #3 took a few seconds, whereas the time for Methods #1 and #2 on graphs of such size would be less than a millisecond.
Each of the three methods of analogy determines a mapping of one CG to another. The first two methods determine a node-by-node mapping of CGs, where some or all of the nodes of the first CG may have different type labels from the corresponding nodes of the other. Method #3 determines a more complex mapping, which comprises multiple mappings of subgraphs of one CG to subgraphs of the other. These methods can be applied to CGs derived from any source, including natural languages, logic, or programming languages.
In one major application, VAE was used to analyze the programs and documentation of a large corporation, which had systems in daily use that were up to forty years old (LeClerc & Majumdar 2002). Although the documentation specified how the programs were supposed to work, nobody knew what errors, discrepancies, and obsolete business procedures might be buried in the code. The task required an analysis of 100 megabytes of English, 1.5 million lines of COBOL programs, and several hundred control-language scripts, which called the programs and specified the data files and formats. Over time, the English terminology, computer formats, and file names had changed. Some of the format changes were caused by new computer systems and business practices, and others were required by different versions of federal regulations. In three weeks of computation on a 750 MHz Pentium III, VAE combined with the Intellitex parser was able to analyze the documentation and programs, translate all statements that referred to files, data, or processes in any of the three languages (English, COBOL, and JCL) to conceptual graphs, and use the CGs to generate an English glossary of all processes and data, to define the specifications for a data dictionary, to create dataflow diagrams of all processes, and to detect inconsistencies between the documentation and the implementation.
Most theorem provers use a tightly constrained version of structure mapping called unification, which forces two structures to become identical. Relaxing constaints in one direction converts unification to generalization, and relaxing them in another direction leads to specialization. With arbitrary combinations of generalization and specialization, there is a looser kind of similarity, which, if there is no limit on the extent, could map any graph to any other. When Peirce's rules of inference are redefined in terms of generalization and specialization, they support an inference procedure that can use exactly the same algorithms and data structures designed for the VivoMind Analogy Engine. The primary difference between the analogy engine and the inference engine is in the strategy that schedules the algorithms and determines which constraints to enforce.
When Peirce invented the implication operator for Boolean algebra, he observed that the truth value of the antecedent is always less than or equal to the truth value of the consequent. Therefore, the symbol ≤ may be used to represent implication: p≤q means that the truth value of p is less than or equal to the truth value of q. That same symbol may be used for generalization: if a graph or formula p is true in fewer cases than another graph or formula q, then p is more specialized and q is more generalized. Figure 8 shows a generalization hierarchy in which the most general CG is at the top. Each dark line in Figure 8 represents the ≤ operator: the CG above is a generalization, and the CG below is a specialization.

Figure 8: A generalization hierarchy of CGs
The top CG says that an animate being is the agent of some act that has an entity as the theme of the act. Below it are two specializations: a CG for a robot washing a truck, and a CG for an animal chasing an entity. The CG for an animal chasing an entity has three specializations: a human chasing a human, a cat chasing a mouse, and the dog Macula chasing a Chevrolet. The two graphs at the bottom represent the most specialized sentences: The cat Yojo is vigorously chasing a brown mouse, and the cat Tigerlily is chasing a gray mouse.
The operations on conceptual graphs are based on combinations of six canonical formation rules, which perform the structure-building operations of perception and the structure-mapping operations of analogy. Logically, each rule has one of three possible effects on a CG: the rule can make it more specialized, more generalized, or logically equivalent but with a modified shape. Each rule has an inverse rule that restores a CG to its original form. The inverse of specialization is generalization, the inverse of generalization is specialization, and the inverse of equivalence is another equivalence.
All the graphs in Figure 8 belong to the existential-conjunctive subset of logic, whose only operators are the existential quantifier ∃ and the conjunction ∧. For this subset, the canonical formation rules take the forms illustrated in Figures 5, 6, and 7. These rules are fundamentally graphical: they are easier to show than to describe. Sowa (2000) presented the formal definitions, which specify the details of how the nodes and arcs are affected by each rule.

Figure 9: Copy and simplify rules
Figure 9 shows the first two rules: copy and simplify. At the top is a CG for the sentence "The cat Yojo is chasing a mouse." The down arrow represents two applications of the copy rule. The first copies the Agnt relation, and the second copies the subgraph →(Thme)→[Mouse]. The two copies of the concept [Mouse] at the bottom of Figure 9 are connected by a dotted line called a coreference link; that link, which corresponds to an equal sign = in predicate calculus, indicates that both concepts must refer to the same individual. Since the new copies do not add any information, they may be erased without losing information. The up arrow represents the simplify rule, which performs the inverse operation of erasing redundant copies. The copy and simplify rules are called equivalence rules because any two CGs that can be transformed from one to the other by any combination of copy and simplify rules are logically equivalent. The two formulas in predicate calculus that are derived from Figure 9 are also logically equivalent. The top CG maps to the following formula:
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z)),In the formula that corresponds to the bottom CG, the equality z=w represents the coreference link that connects the two copies of [Mouse]:
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(∃w:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ agnt(y,x) ∧ thme(y,z) ∧ thme(y,w) ∧ z=w).By the inference rules of predicate calculus, either of these two formulas can be derived from the other.
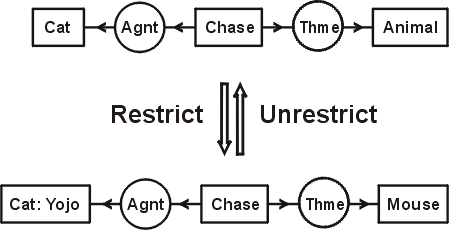
Figure 10: Restrict and unrestrict rules
Figure 10 illustrates the restrict and unrestrict rules. At the top is a CG for the sentence "A cat is chasing an animal." Two applications of the restrict rule transform it to the CG for "The cat Yojo is chasing a mouse." The first step is a restriction by referent of the concept [Cat], which represents some indefinite cat, to the more specific concept [Cat: Yojo], which represents a particular cat named Yojo. The second step is a restriction by type of the concept [Animal] to a concept of the subtype [Mouse]. Two applications of the unrestrict rule perform the inverse transformation of the bottom graph to the top graph. The restrict rule is a specialization rule, and the unrestrict rule is a generalization rule. The more specialized graph implies the more general one: if the cat Yojo is chasing a mouse, it follows that a cat is chasing an animal. The same implication holds for the corresponding formulas in predicate calculus. The more general formula
(∃x:Cat)(∃y:Chase)(∃z:Animal)(agnt(y,x) ∧ thme(y,z))
is implied by the more specialized formula
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z)).

Figure 11: Join and detach rules
Figure 11 illustrates the join and detach rules. At the top are two CGs for the sentences "Yojo is chasing a mouse" and "A mouse is brown." The join rule overlays the two identical copies of the concept [Mouse], to form a single CG for the sentence "Yojo is chasing a brown mouse." The detach rule performs the inverse operation. The result of join is a more specialized graph that implies the one derived by detach. The same implication holds for the corresponding formulas in predicate calculus. The conjunction of the formulas for the top two CGs
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z))is implied by the formula for the bottom CG(∃w:Mouse)(∃v:Brown)attr(w,v)
(∃x:Cat)(∃y:Chase)(∃z:Mouse)(∃v:Brown)(name(x,'Yojo') ∧ agnt(y,x) ∧ thme(y,z) ∧ attr(z,v)).
These rules can be applied to full first-order logic by specifying how they interact with negation. In CGs, each negation is represented by a context that has an attached relation of type Neg or its abbreviation by the symbol ¬ or ~. A positive context is nested in an even number of negations (possibly zero). A negative context is nested in an odd number of negations. The following four principles determine how negations affect the rules:
By handling the syntactic details of conceptual graphs, the canonical formation rules enable the rules of inference to be stated in a form that is independent of the graph notation. For each of the six rules, there is an equivalent rule for predicate calculus or any other notation for classical FOL. To derive equivalent rules for other notations, start by showing the effect of each rule on the existential-conjunctive subset (no operators other than ∃ and ∧). To handle negation, add one to the negation count for each subgraph or subformula that is governed by a ~ symbol. For other operators (∀, ⊃, and ∨), count the number of negations in their definitions. For example, p⊃q is defined as ~(p∧~q); therefore, the subformula p is nested inside one additional negation, and the subformula q is nested inside two additional negations.
When the CG rules are applied to other notations, some extensions may be necessary. For example, the blank or empty graph is a well-formed EG or CG, which is always true. In predicate calculus, the blank may be represented by a constant formula T, which is defined to be true. The operation of erasing a graph would correspond to replacing a formula by T. When formulas are erased or inserted, an accompanying conjunction symbol must also be erased or inserted in some notations. Other notations, such as the Knowledge Interchange Format (KIF), are closer to CGs because they only require one conjunction symbol for an arbitrarily long list of conjuncts. In KIF, the formula (and), which is an empty list of conjuncts, may be used as a synonym for the blank graph or T. Discourse representation structures (DRSs) are even closer to EGs and CGs because they do not use any symbol for conjunction; therefore, the blank may be considered a DRS that is always true.
Peirce's rules, which he stated in terms of existential graphs, form a sound and complete system of inference for first-order logic with equality. If the word graph is considered a synonym for formula or statement, the following adaptation of Peirce's rules can be applied to any notation for FOL, including EGs, CGs, DRS, KIF, or the many variations of predicate calculus. These rules can also be applied to subsets of FOL, such as description logics and Horn-clause rules.
These rules, which Peirce formulated in several equivalent variants from 1897 to 1909, form an elegant and powerful generalization of the rules of natural deduction by Gentzen (1935). Like Gentzen's version, the only axiom is the blank. What makes Peirce's rules more powerful is the option of applying them in any context nested arbitrarily deep. That option shortens many proofs, and it eliminates Gentzen's bookkeeping for making and discharging assumptions. For further discussion and comparison, see MS 514 (Peirce 1909) and the commentary that shows how other rules of inference can be derived from Peirce's rules.
Unlike most proof procedures, which are tightly bound to a particular syntax, this version of Peirce's rules is stated in notation-independent terms of generalization and specialization. In this form, they can even be applied to natural languages. For any language, the first step is to show how each syntax rule affects generalization, specialization, and equivalence. In counting the negation depth for natural languages, it is important to recognize the large number of negation words, such as not, never, none, nothing, nobody, or nowhere. But many other words also contain implicit negations, which affect any context governed by those words. Verbs like prevent or deny, for example, introduce a negation into any clause or phrase in their complement. Many adjectives also have implicit negations: a stuffed bear, for example, lacks essential properties of a bear, such as being alive. After the effects of these features on generalization and specialization have been taken into account in the syntactic definition of the language, Peirce's rules can be applied to a natural language as easily as to a formal language.
Peirce developed his theory of signs or semeiotic as a species-independent theory of cognition. He considered it true of any "scientific intelligence," by which he meant any intelligence that is "capable of learning from experience." Peirce was familiar with Babbage's mechanical computer; he was the first person to suggest that such machines should be based on electical circuits rather than mechanical linkages; and in 1887, he published an article on "logical machines" in the American Journal of Psychology, which even today would be a respectable commentary on the possibilities and difficulties of artificial intelligence. His definition of sign is independent of any implementation in proteins or silicon:
I define a sign as something, A, which brings something, B, its interpretant, into the same sort of correspondence with something, C, its object, as that in which itself stands to C. In this definition I make no more reference to anything like the human mind than I do when I define a line as the place within which a particle lies during a lapse of time. (1902, p. 235)As a close friend of William James, Peirce was familiar with the experimental psychology of his day, which he considered a valuable study of what possibilities are realized in any particular species. But he considered semeiotic to be a more fundamental, implementation-independent characterization of cognition.
Peirce defined logic as "the study of the formal laws of signs" (1902, p. 235), which implies that it is based on the same kinds of semeiotic operations as all other cognitive processes. He reserved the word analogy for what is called "analogical reasoning" in this paper. For the kinds of structure mapping performed by SME and VAE, Peirce used the term diagrammatic reasoning, which he described as follows:
The first things I found out were that all mathematical reasoning is diagrammatic and that all necessary reasoning is mathematical reasoning, no matter how simple it may be. By diagrammatic reasoning, I mean reasoning which constructs a diagram according to a precept expressed in general terms, performs experiments upon this diagram, notes their results, assures itself that similar experiments performed upon any diagram constructed according to the same precept would have the same results, and expresses this in general terms. This was a discovery of no little importance, showing, as it does, that all knowledge without exception comes from observation. (1902, pp. 91-92)This short paragraph summarizes many themes that Peirce developed in more detail in his other works. In fact, it summarizes the major themes of this article:
For natural language understanding, the constrained operations of unification and generalization are important, but exceptions, metaphors, ellipses, novel word senses, and the inevitable errors require less constrained analogies. When the VAE algorithms are used in the semantic interpreter, there are no exceptions: analogies are used at every step, and the only difference between unification, generalization, and looser similarities is the nature of the constraints on the analogy.
Chalmers, D. J., R. M. French, & D. R. Hofstadter (1992) "High-level perception, representation, and analogy: A critique of artificial intelligence methodology," Journal of Experimental & Theoretical Artificial Intelligence 4, 185-211.
Falkenhainer, B., Kenneth D. Forbus, Dedre Gentner (1989) "The Structure mapping engine: algorithm and examples," Artificial Intelligence 41, 1-63.
Forbus, Kenneth D., Dedre Gentner, & K. Law (1995) "MAC/FAC: A Model of Similarity-Based Retrieval," Cognitive Science 19:2, 141-205.
Forbus, Kenneth D., Dedre Gentner, Arthur B. Markman, & Ronald W. Ferguson (1998) "Analogy just looks like high level perception: Why a domain-general approach to analogical mapping is right," Journal of Experimental & Theoretical Artificial Intelligence 10:2, 231-257.
Forbus, Kenneth D., T. Mostek, & R. Ferguson (2002) "An analogy ontology for integrating analogical processing and first-principles reasoning," Proc. IAAI-02 pp. 878-885.
Gentzen, Gerhard (1935) "Untersuchungen über das logische Schließen," translated as "Investigations into logical deduction" in The Collected Papers of Gerhard Gentzen, ed. and translated by M. E. Szabo, North-Holland Publishing Co., Amsterdam, 1969, pp. 68-131.
Hallaq, Wael B. (1993) Ibn Taymiyya Against the Greek Logicians, Clarendon Press, Oxford.
LeClerc, André, & Arun Majumdar (2002) "Legacy revaluation and the making of LegacyWorks," Distributed Enterprise Architecture 5:9, Cutter Consortium, Arlington, MA.
Morrison, Clayton T., & Eric Dietrich (1995) "Structure-mapping vs. high-level perception: the mistaken fight over the explanation of Analogy," Proc. 17th Annual Conference of the Cognitive Science Society, pp. 678-682. Available at http://babs.cs.umass.edu/~clayton/CogSci95/SM-v-HLP.html
Peirce, Charles Sanders (1887) "Logical machines," American Journal of Psychology, vol. 1, Nov. 1887, pp. 165-170.
Peirce, Charles S. (1902) Logic, Considered as Semeiotic, MS L75, edited by Joseph Ransdell, http://members.door.net/arisbe/menu/library/bycsp/l75/l75.htm
Peirce, Charles Sanders (1909) Manuscript 514, with commentary by J. F. Sowa, available at http://www.jfsowa.com/peirce/ms514.htm
Sowa, John F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole Publishing Co., Pacific Grove, CA.