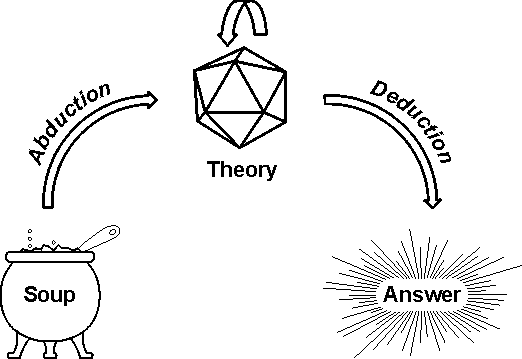
Figure 1: Crystallizing theories out of knowledge soup
Abstract. In very large knowledge bases, global consistency is almost impossible to achieve, yet local consistency is essential for deduction and problem solving. To preserve local consistency in an environment of global inconsistency, this article proposes a two-level structure: a large reservoir of loosely organized encyclopedic knowledge, called knowledge soup; and floating in the soup, much smaller, tightly organized theories that resemble the usual microworlds of AI. The two kinds of knowledge require two distinct kinds of reasoning: abduction uses associative search, measures of salience, and theory revision for finding chunks of knowledge in the soup and assembling them into consistent theories; and deduction uses theorem-proving techniques for reasoning within a theory. The resulting two-level system can attain the goals of nonmonotonic logic, while retaining the simplicity of classical logic; it can use statistics for dealing with uncertainty, while preserving the precision of logic in dealing with hard-edged facts; and it can relate logics with discrete symbols to models of continuous systems.
Pulished in Intelligent Systems: State of the Art and Future Directions, edited by Zbigniew W. Ras and Maria Zemankova, Ellis Horwood, New York, 1990, pp. 456-487. For a major update and extension of this paper, see "The Challenge of Knowledge Soup".
Much of the knowledge in people's heads is inconsistent. Some of it may be represented in symbolic or propositional form, but a lot of it or perhaps even most of it is stored in image-like forms. And some knowledge is stored in vague "gut feel" or intuitive forms that are almost never verbalized. The term knowledge base sounds too precise and organized to reflect the enormous complexity of what people have in their heads. The term knowledge soup more clearly suggests its heterogeneous nature. The soup may contain many small chunks, corresponding to the typical frames, rules, and facts in AI systems; and it may also contain large chunks that correspond to entire theories. The chunks should be internally consistent, but they may be inconsistent with one another. The inconsistencies arise from various sources:
Since the inconsistencies are most common in ordinary speech, many people assume that they are merely linguistic problems that would not occur in a purified language like logic. Yet that assumption is wrong. All of those problems are caused by the complexity of the world itself. A logical predicate like body-part(x) would solve nothing; the intermediate cases of hair and fingernails would raise the same questions of truth and falsity as the English noun phrase body part. Some of the vagueness results from a mismatch of the continuous world with the discrete set of words in language or predicates in logic:
Any mechanically embodied intelligent process will be comprised of structural ingredients that (a) we as external observers naturally take to represent a propositional account of the knowledge that the overall process exhibits, and (b) independent of such external semantical attribution, play a formal but causal and essential role in engendering the behavior that manifests that knowledge.The view of knowledge as a collection of propositions characterizes the discrete, symbolic systems of AI. But it is incompatible with Wittgenstein's family resemblances, Waismann's open textures, and any other view that considers continuity to be an essential and irreducible aspect of the world. A more general hypothesis is Craik's view (1952) of the brain as a machine for making models:
If the organism carries a small-scale model of external reality and of its own possible actions within its head, it is able to carry out various alternatives, conclude which is the best of them, react to future situations before they arise, utilize the knowledge of past events in dealing with the present and the future, and in every way react in a fuller, safer, and more competent manner to the emergencies which face it.Craik's view has been widely accepted since its introduction to the AI community by Minsky (1965). It includes Smith's hypothesis as a special case where the models happen to be built from discrete logical elements. But Craik's models are more general. They permit continuous models, numeric computations, and even nonnumeric images. For continuously varying quantities, it is more accurate to model a situation with differential equations than to prove theorems from a set of propositions. Research in qualitative physics uses symbolic methods to reason about physical situations. Those methods can "explain" why a given quantity may be positive or negative, but to compute its exact value, the symbolic methods must be supplemented with a much more detailed numeric computation.
Many aspects of intelligent behavior require constant interaction between continuous and discrete representations. A basketball player, for example, may think in propositions like We are 10 points ahead, and the game is almost over. Therefore, we should "freeze" the ball to prevent the other team from scoring. But when the same player shoots the ball at the basket, his arm movements can be computed more easily by numeric simulations than by logical deductions. For such problems, some programs simulate continuous structures with iconic or image-like "diagrams". Instead of proving theorems about the structures, they simply measure the diagrams. As an example, consider the following instructions for building a geometric model:
As this discussion indicates, the problems with knowledge soup arise from the complexity of the world. No version of logic with discrete symbols can represent all the richness of a continuous system. Yet discrete logics are the best systems available for precise reasoning, planning, and problem solving. They are also necessary for language, since every human language is based on a discrete, finite set of words or morphemes. To accommodate the continuous and the discrete, this article proposes a two-phase model of reasoning: the first phase, called abduction, extracts precise, discrete theories out of the continuities and uncertainties of knowledge soup; the second phase, called deduction, uses a more classical kind of logic to reason within a theory constructed by abduction. The next two sections of this article discuss statistics and nonmonotonic logics, which include techniques that may be used in abduction. Section 4 shows how abduction and deduction could be applied to various problems, and the remaining sections discuss ways of integrating the two kinds of reasoning in AI systems.
Statistics includes some of the oldest and best developed theories for dealing with knowledge soup. When a situation has confusing aspects that cannot easily be sorted out, statistical techniques of factor analysis and clustering can help to determine the ones that have the greatest effect. Connectionism is a popular statistical technique with an intuitively attractive relationship to brain models. But all statistical approaches, including connectionism, have limitations:
On the border between logic and statistics are fuzzy logic and fuzzy set theory (Zadeh 1974), which were designed for reasoning about phenomena with a high degree of uncertainty. Instead of saying categorically that all Quakers are pacifists, one might say that Quakers are very likely to be pacifists. Terms like "likely" or "very likely" are assigned numeric certainty factors, which can vary along a continuum from –1 for false to +1 for true. (Some versions use may use a different range of values, but the principles are the same.) These values are not probabilities, but degrees of certainty, which a person might feel intuitively. In fuzzy logic, the argument about Nixon might be: Quakers are pacifists (certainty 0.8); Republicans are not pacifists (certainty 0.8); Nixon is a Republican (certainty 0.9) and a Quaker (certainty 0.7); therefore, Nixon is a nonpacifist with certainty 0.72 (0.8 times 0.9) and a pacifist with certainty 0.56. By representing intuitive judgments, fuzzy logic can sometimes handle situations with insufficient data for the usual statistical tests. It has also been used to represent the interactions between a continuous system and discrete propositions; its most successful applications have been in control systems for trains, elevators, and automatic transmissions.
Despite some useful applications, the foundations of fuzzy logic have been severely criticized. Certainty factors are neither truth values nor probabilities, and no satisfactory model theory has been developed for them. There is an abundance of proposals for computing with certainty factors, but a shortage of convincing reasons for preferring one to another. Of the five kinds of problems with knowledge soup, fuzzy logic cannot solve any of them completely:
In analyzing methods for reasoning about uncertainty, Pearl (1988) distinguished two kinds of approaches: extensional approaches calculate a certainty factor for a proposition independent of its meaning; and intensional approaches require a deeper analysis of the meaning before determining the certainty. In fuzzy logic, for example, the usual rule for computing the certainty of a disjunction A∨B depends only on the certainty of A and the certainty of B:
C(A ∨ B) = max(C(A),C(B)).This is an extensional rule, since it does not depend on the meanings of A and B or on any interaction between A and B. By contrast, the rule for computing the probability of A∨B is more complex:
P(A ∨ B) = P(A) + P(B) − P(A ∧ B).This formula says that the probability of A∨B is not just a function of the probabilities of A and B; it also depends on the probability of A∧B, which cannot be determined without further knowledge of the meanings of A and B. For this reason, conventional probability theory may be called intensional.
Many expert systems use fuzzy logic rather than probabilities because extensional computations are easier to perform. Yet such easily computed numbers are subject to anomalies and paradoxes that often make them misleading or simply wrong. Connectionism is somewhere between the intensional and extensional approaches: neural networks could be trained to respond only to certainty factors and would therefore compute results similar to fuzzy logic; but they could also be trained on many different aspects of situations, including ones that relate to structure, purpose, and other intensional properties. Yet as connectionist networks become more complex, it becomes harder to analyze exactly what they are responding to and the real meaning of what they are computing.
Statistics, connectionism, and fuzzy logic can handle some of the uncertainties, but they are poorly suited to hard-edged, precise reasoning. In designing an automobile, for example, engineers have to make many decisions about possible alternatives. For each decision, statistics can help to evaluate the alternatives and estimate the failure rates. But after a decision is made, uncertainty vanishes; there is no such thing as an "average" car with 4.79 cylinders and 2.38-wheel drive. Although statistics may be important for evaluating design decisions, it cannot replace hard-edged logic for designing a structure and reasoning about it.
Classical logic is monotonic: adding propositions to a theory monotonically increases the number of theorems that can be proved. If a theory implies that you can drive from New York to Boston, new information about a dead battery or snow conditions can never block the proof. If a contradiction arises, the old proofs are not blocked; instead, everything becomes provable. For these reasons, many AI researchers reject classical logic, both as a psychological model of human thinking and as a basis for practical AI systems. There are two ways of rejecting classical logic:
The informal methods include Minsky's frames (1975), Schank and Abelson's scripts (1977), and related methods for showing typical, default, or expected information. The main weakness of the informal methods is that they were never defined precisely. Minsky and Schank presented a variety of stimulating examples in their papers, but they never formulated exact definitions that completely characterized them. As examples, consider the following frames, which were taken from an AI textbook:
[frame: bird
isa: vertebrate
slots: (covering (default feathers))
(reproduces-by (default lays-eggs))
(flies (default t))]
[frame: penguin
isa: bird
slots: (flies (default nil))]
The first frame says that the default value of the "flies" slot
for the bird frame is the truth value t. The second frame says that
a penguin is a subtype of bird; therefore, it inherits all the slots and
defaults in the bird frame except the default for "flies," which
is redefined to be nil. Together, these two frames are supposed to
imply that birds normally fly, but penguins don't.
Frames are popular because they are considered to be powerful and easy to learn. Yet those properties are illusory. The power of frame systems arises from their associated procedural languages, which are as general as a Turing machine. They are easy to learn because there are no rules for what can be used as slot names or the values that go in the slots. In this example, there are three slot names: "covering" is a participle whose associated value is a plural noun; "reproduces-by" is a verb-preposition pair whose value is a gerund-noun pair; and "flies" is a verb whose value is t or nil. The meaning of a frame is not defined by any systematic relationship to logic, language, or the real world; it is defined only by the procedures that manipulate the character strings in the slots, and they are allowed to do anything at all. Commercial frame systems are larger and more complex than this toy example, but they are no more precise. Indeed, they have more ad hoc features that make them even more susceptible to errors and anomalies, as various critics have pointed out (Brachman 1985; Twine 1990).
With their intuitive insights, Minsky and Schank were trying to express something important, but the actual systems implemented by their students never matched the richness of their original vision. Minsky's wealth of insights dissipated in expert systems where frames became little more than records with pointers to other records. Schank's original scripts were simplified to "sketchy scripts" for better efficiency and later to LISP data structures that were indistinguishable from what became of Minsky's frames. Schank's (1982) later structures, his MOPs and TOPs, were more generalized and modular than scripts, but they were no more precisely defined. For all of them, programmers wrote unmaintainable LISP code to manipulate the data structures. Good intuitions may be stimulating, but without a precise formalism, they cannot control the complexity of the knowledge soup.
Meanwhile, formalists tried to maintain the precision of classical logic, while changing the inference methods to overcome the limitations. One of the best known approaches is Reiter's default logic (1980). Default rules have the following form:
This rule says that if some predicate α is true of x and it is consistent to believe β(x), then conclude γ(x). For the example of driving the car to Boston, α(x) might be the statement "x is a car"; β(x) might be "x has all parts in working order"; and γ(x) might be the conclusion "x can be driven from New York to Boston." Therefore, if you have a car for which none of the conditions in β are violated, you could assume that you could drive it to Boston. But if you later discovered that the battery was dead, then the conclusion would be blocked. By allowing new information to block a conclusion, default rules provide a nonmonotonic effect.
Default logic was designed to handle exceptions to general propositions. But it runs into difficulties with conflicting defaults. As an example, consider the following default rule:
This rule says that if x is a Quaker and it is consistent to believe that x is a pacifist, then conclude that x is a pacifist. Then the following rule says that if x is a Republican and it is consistent to believe that x is not a pacifist, then conclude that x is not a pacifist.
Now suppose new information is added about Nixon being both a Republican and a Quaker. If the first rule happened to be executed first, the conclusion would be pacifist(Nixon), and the second rule would be blocked. But if the second rule happened to be executed first, the conclusion would be ~pacifist(Nixon), and the first rule would be blocked. Such a system would maintain consistency, but its results would be unpredictable. Reiter and Criscuolo (1981) acknowledge the difficulties; they admit that default theories are complicated and that interacting defaults make them even more so.
Another weakness of default logic is intractability. In conventional logic, the rule of modus ponens requires a pattern match that can be done in linear time. Yet even if each rule takes linear time, a complete proof could take exponential time because a very large number of rules may be executed. In default logic, however, each rule itself requires a consistency check that could be as complex as an entire proof in conventional logic. A proof with defaults might therefore require an exponential number of rules, each of which could take exponential time. The computations are so staggeringly complex that no one has ever applied default logic to anything more than toy examples. As Israel (1980) said, "Why such a beast is to be called a logic is somewhat beyond me."
In contrast with the complexity of default logic, frame systems are usually quite efficient. Inheritance allows an inference to be performed just by following a chain of pointers and copying some data. A default simply cancels one value and replaces it with another; even interacting defaults can be handled fairly well, and the underlying logic of inheritance can be developed in a formally respectable way (Thomason and Touretzky 1990). Yet that efficiency is purchased at the expense of reduced expressive power: many kinds of inferences cannot be handled by inheritance alone. If frame-like inheritance were the only inference rule, default logic could also do consistency checks in linear time and run nearly as fast as a frame system. There is no magic: frame notation cannot solve an unsolvable problem; it merely limits the expressive power so that the difficult questions cannot be asked.
Some form of nonmonotonic reasoning is necessary, but Israel was right in questioning whether it should be called "logic." There are many versions of logic — classical, intuitionistic, relevance, modal, intensional, and higher-order — yet all of them share a common spirit and a common notion of what a rule of inference should be. By requiring a consistency check for every application of a default rule, the nonmonotonic logicians have broken with the tradition that rules of inference should be simple and mechanical. McCarthy's theory of circumscription (1980) is a method of minimizing over models that is more explicitly a method of theory creation or modification than a rule of inference. He explicitly refused to call it a logic: "Circumscription is not a "nonmonotonic logic." It is a form of nonmonotonic reasoning augmenting first-order logic.... In our opinion, it is better to avoid modifying the logic if at all possible, because there are many temptations to modify the logic, and it would be difficult to keep them compatible." This view is compatible with the methods of theory revision proposed by Levi (1980), which provide a nonmonotonic effect while retaining the simplicity of first-order logic.
The philosopher and logician Charles Sanders Peirce coined the term abduction for the process of generating hypotheses, whose consequences are later explored by deduction. The term has been adopted by AI researchers for an initial stage of hypothesis formation to be followed by a later stage of deduction from the hypotheses. In this article, abduction is defined as the process of selecting chunks of knowledge from the soup, evaluating their relevance to the problem at hand, and assembling them into a consistent theory. Abduction may be performed at various levels of complexity:

Figure 1: Crystallizing theories out of knowledge soup
As an example, consider a bridge player who is planning a line of play. The knowledge soup for bridge includes tactics like finesses and endplays, probability estimates for various card distributions, and techniques for analyzing a given bridge hand to find an optimal line of play. In double-dummy bridge (where all 52 cards are arranged face up), there is no uncertainty, and success depends only on precise reasoning. But in a normal game, each player sees half of the cards dealt, and the distribution of the remaining cards must be guessed from probabilities and hints from the bidding and play. In planning the play, a bridge player combines abduction and deduction:
The bridge example illustrates how abduction could use statistics for dealing with uncertainty, while deduction uses precise logic. The two phases of reasoning may be stated more generally:
As another example of abduction and deduction, consider whether Nixon is a pacifist. The two phases in the reasoning process would proceed as follows:
For the problem about driving to Boston, the initial theory would include only the most salient propositions:
One of the long-time advocates of abduction in expert systems has been Pople (1975, 1982), who has used abduction for hypothesis generation and selection in the medical diagnostic systems DIALOG, INTERNIST, and CADUCEUS. The DIALOG system used the simplest version of abduction, which evaluated the relevance of several predefined hypotheses. In measuring the relevance of a hypothesis, DIALOG added points for implications that were observed, and subtracted points for implications that were not observed. The additions and subtractions were weighted by a measure of the importance of each observation. In the INTERNIST-II and CADUCEUS systems, the abduction phase was extended to combine hypotheses when multiple diseases might be present simultaneously. In all of these systems, however, the possible hypotheses were given in advance, and none of them used theory revision to handle complex abduction.
Uncertainty is common in medical diagnosis, but even physics, the hardest of the "hard" sciences, requires a stage of model building where approximation is essential. In calculating the orbit of a satellite, relativity and quantum mechanics are ignored; the influences of the earth, moon, and sun are significant, but the other planets and asteroids are ignored. In thermodynamics, individual molecules are ignored, and temperature, pressure, entropy, and other quantities depend on averages of sextillions of molecules. In fluid mechanics, the equations are so difficult to evaluate that every application requires major simplifications. For most subsonic flows, even air is treated as an incompressible fluid. One nineteenth-century physicist "proved" that it was impossible for anything to travel faster than the speed of sound; his proof depended on someone else's simplified equations for velocities that were much less than the speed of sound.
As these examples illustrate, physics is not a monolithic subject, but a loose collection of subfields, each characterized by what it ignores or approximates. The totality forms an inconsistent knowledge soup, where one scientist ignores features that are the focus of attention for another. In every subfield, problem solving requires an abductive stage of model building where relevant knowledge is selected, details are ignored, and irregular features are approximated by simpler structures. Reasoning only becomes precise, formal, and deductive after the intractable details have been thrown away: a boulder tumbling down a mountainside becomes a sphere rolling down a cone.
Abduction extracts relevant chunks from the knowledge soup to construct a theory that makes deduction possible. Yet what is relevant depends critically on the application. When the boulder is rolling down the mountain, its relevant features are roundness, radius, mass, and moment of inertia. A sphere is the simplest approximation for which those features are easy to compute and relate to one another. But in another application, that same boulder might be used to build a wall, where its sharp corners become significant. For that purpose, it might be better approximated as a rectangular building block. Note the key terms in this discussion: purpose, relevance, and approximation. In trying to define abduction, many AI researchers ignore them because they spoil the parallels with induction and deduction. Following are the common definitions:
Abduction also requires an implicit universal quantifier. If β is true, abduction should not pick an arbitrary α that happens to imply β. Instead, it should select the best α out of all possible explanations for β that are consistent with what is currently believed. Following is a definition of abduction adapted from Zadrozny (forthcoming), who generalized several earlier proposals (Reggia et al. 1983; Poole 1989; Levesque 1989): Let T be a theory that is believed to hold, and β an observation that is to be explained by extending T. Then define S as the set of all possible formulas that could be candidates for such an extension of T:
S = { α | T ∧ α ∧ β is consistent; T, α |− β }.This says that S is the set of all α consistent with T and β such that β is provable from T and α. Each α is a potential explanation for β, but not all of them are equally good. Zadrozny assumes a preference relation that defines a partial ordering over S. Abduction then selects the α in S with the highest preference. If α1 and α2 have equal preference, it would have to select one of them.
The preference relation is at the heart of some of the most serious controversies about abduction. Some characteristics are widely accepted: if α1 implies α2 and α2 implies β, then α2 is a more direct, hence more preferred explanation for β than α1. But β itself implies β, and nothing else could be more direct. Such trivial explanations can be eliminated by ruling out those that are logically equivalent to the observation. Yet suppose β is the observation "I see cat prints on my car." The immediate explanation is that a cat was walking across the car. That explanation, although not logically equivalent to β, is still rather trivial. A better explanation would be "It's probably the little mottled cat from next door, because I often see her in the driveway." This explanation is preferred because it also takes into account other cat sightings. One might counter that those other sightings should have been included as part of the original observation β. In general, however, there is no way to predict exactly which facts should be considered relevant. In science, medicine, and detective stories, the number of seemingly unrelated facts is enormous. Only after a theory has been proposed can relevant observations be distinguished from incidental details.
As another criterion for the preference relation, a small simple α is usually better, but it is not clear how size and simplicity should be measured. The story that God created heaven and earth in six days is shorter and simpler than the big bang theory plus evolution plus all the rest of science. Yet that seemingly simple assumption must be supplemented with additional assumptions for each star and planet, each species of plant and animal, and even each type of organ in each species. When all those additional assumptions are considered, the original simplicity vanishes. Besides simplicity, the preference relation may have to take into account external factors such as purpose and relevance. For one purpose, a boulder may be better approximated as a sphere; for another purpose, as a rectangular block.
Another issue to consider is the method of computing or selecting the propositions in S. In the examples cited in AI papers, S is finite, and quantification over "all possible" explanations is easy. But in real life, the number of possible explanations may be open ended, even nondenumerable, and subject to all the ambiguities and uncertainties of knowledge soup. Even a single α might be difficult to compute, especially if it happened to be a brilliant idea that might not occur to anyone for centuries to come. Finally, the selection of the starting theory T could create difficulties. An engineer might know all the standard theories of fluid mechanics, yet not know which simplifying assumptions to make in order to solve a particular problem.
A more general form of abduction should treat it as a process of theory creation or modification rather than a "logic" for deriving propositions. As before, let T be an initial theory and β some observations. To capture the notion of purpose, let γ(x) be some goal to be satisfied. The goal γ may represent a problem for which x is the solution: T may be a medical theory, β the symptoms, and x the prescribed therapy. For a planning system, the answer x might be a sequence of operations: if γ(x) is the goal of driving to Boston and β is an observation that the battery is dead, then x might be instructions for repairing the car followed by directions for driving to Boston. If the original T contained sufficient information, the goal γ(x) could be computed in the same way that Prolog responds to a goal. But in general, T might not be consistent with β, or it might not contain sufficient information to answer γ. Abduction is the process of revising T to form a consistent theory T′ from which the observation β and some x that satisfies the goal γ(x) are both derivable:
T′ is consistent, T′ |− β, and T′ |− (∃x)γ(x).If more than one T′ meets these conditions, a preference relation is necessary to choose between them. In extending T, minimal changes should be preferred, and any additions should come from the background knowledge soup K. There should also be a preference for increased explanatory power: if T′ implies some proposition in K that was not implied by T, then its preference is enhanced. The more chunks in K that are implied by a theory, the more effectively it crystallizes knowledge in a form that is suitable for deduction and problem solving.
The goal γ and the background knowledge K help to meet the objections to the earlier definitions. For the cat prints on the car, an explanation that takes into account a larger amount of background knowledge might be preferable, even though that knowledge was not included in the original observation β. For the boulder rolling down the mountain, which theory is chosen might depend on whether the goal γ is to compute its speed or to determine where to place it in building a wall. For the story of creation, the starting theory T might depend on a person's previous education in science and religion; it might also depend on whether the goal γ is to determine moral conduct in life or to compute the rate of expansion of the universe.
In revising a theory T, any proposition in the knowledge soup could be added to form a new theory T′. Yet additions alone cannot provide a nonmonotonic effect; deletions are necessary when an inconsistency arises. The logical and philosophical basis of theory revision has been developed by Levi (1980) and by Gärdenfors (1988) and his colleagues. Gärdenfors's axioms allow T to be contracted in case the new knowledge contradicts something in the old theory. Systems based on those axioms have been implemented by Rao and Foo (1989a,b). Once a theory T has been created, reasoning within T is done by purely classical logic. If contradictions or limitations are found, T may be revised or replaced with a better theory, and further reasoning remains classical. Although classical logic is monotonic, a nonmonotonic effect can be achieved by metalevel reasoning about theories and by modifying theories as new information is obtained.
Each theory crystallized from the knowledge soup is specialized for a particular observation β and goal γ. With another β and γ, other concepts and chunks of knowledge containing those concepts may increase or decrease in salience. For the concept DOG, the most salient supertype is normally ANIMAL, and other supertypes like CARNIVORE, MAMMAL, and VERTEBRATE are much less likely to be recalled. Yet those other supertypes could increase in salience if the topic concerned diet, lactation, or skeletal structure. For driving a car to Boston, the knowledge soup includes an indefinite amount of knowledge of low salience:
Salience and relevance are informal notions that can be given precise definitions. For any two concepts (or predicates) x and y, let a(x,y) be a measure of association between them; in information retrieval, it is defined in terms of the frequency with which x and y occur in the same context, usually with some adjustment for the the frequencies of x and y by themselves. For any chunk of knowledge p, let P be the set of all concepts in p, and Q the set of all concepts in β, γ, and the starting theory T; then the salience S(p) could be defined as the sum of the associations between concepts in P and concepts in Q:
S(p) = Σx∈P Σy∈Q a(x,y).Whereas salience is a statistical measure, relevance depends on logic. If T is a theory from which β is provable, the set of support for β consists of those propositions in T that are used in a proof of β. Each of those propositions is said to be relevant to the proof. For a given T, β, and γ, it is hoped that the propositions in K with high salience are likely to be relevant additions to T for deriving β and γ. There is some justification for this hope: a proposition of 0 salience is certain to be irrelevant, since it would have no concepts (or predicates) in common with any propositions in T; therefore, it could not interact with them in any rule of inference. Conversely, a proposition with high salience has a good chance of occurring in some line of a proof of β and γ. Although salience does not guarantee relevance, it could quickly eliminate the irrelevant chunks and estimate the importance of the others. Then the slower, but more precise logical techniques could be used to test relevance.
The definition of salience can apply to chunks of knowledge of any size. For familiar situations, the knowledge soup might contain a prefabricated theory T that could immediately determine what to do. If so, T would probably have a high salience, since it would contain many concepts with strong associations to the given β and γ. The notion of universal planning (Schoppers 1987) is based on that possibility: instead of using deductive logic for each situation, a robot might have a cache of prefabricated plans for every circumstance it is likely to encounter. The robot's perceptual inputs could go through an associative network that would select an appropriate plan (i.e. special-purpose theory) that would directly determine its next action. Both the perceptual mechanisms and the associative network might be sensitive to structural features that could determine more than salience: they might even estimate relevance, which would normally require some use of logic.
Universal planning is a controversial idea that was recently debated in AI Magazine (Ginsberg 1989; Chapman 1989; Schoppers 1989). Ginsberg presented several criticisms: it doesn't always work; it requires too much memory to be useful for practical problems; general deduction is still necessary for unanticipated situations; and it "cannot be used as an architecture on which to build a cognitive agent." The theory of knowledge soup can lead to an architecture that meets these criticisms: it requires some kind of associative memory, perhaps a connectionist network, for retrieving theories or fragments of theories at all levels of complexity. For familiar situations, it allows the network to retrieve a reactive plan almost instantaneously. For less familiar situations, the network could retrieve a theory that might require a few seconds or even minutes of deduction to compute a plan. And for unusual cases, it could use abduction to retrieve many fragments of low salience and assemble them into a tailor-made theory for the situation. If some application of a theory T worked successfully for a particular β and γ(x), the answer γ(a) could be stored in the knowledge soup; if a similar β and γ occurred later, the associative network could immediately retrieve γ(a) instead of doing a lengthy deduction from T. In criticizing the memory requirements, Ginsberg claimed that a universal plan might require an exponential amount of time to compute and a correspondingly exponential amount of storage in the cache. Yet a robot need not save all possibilities; it would only need to save those that were useful in the past (and perhaps those that turned out to be disastrous as well). Possibilities grow exponentially, but experience only accumulates linearly with time. If the knowledge soup grows linearly, the kinds of storage devices currently available should be adequate to store it.
Abduction is the kind of process that underlies the creation of scientific theories. Since perfect abduction is noncomputable, perfect science is unattainable, either by computers or by human beings. Instead of leaping from observation to finished theory, science evolves over the centuries with closer and closer approximations that never achieve a perfect match with reality. Although perfect abduction may be impossible, approximations that are adequate for some purpose are attainable by people, and they should be computable by machine. New observations and goals could stimulate abduction to extract an unusual selection of background knowledge and assemble it in novel ways. With a suitable sequence of observations and goals, a system based on abduction could become an evolutionary system for learning and discovery. The goals are an important stimulus to the process: by asking the right sequence of questions, Socrates could get his students to construct new theories for themselves.
In extracting knowledge from the soup, abduction may find relevant chunks that are stored as images or other continuous forms. The problem of relating continuous images to discrete symbols is called symbol grounding (Harnad 1990). Information from the senses enters in image-like icons, which must be interpreted in symbols for language and deduction. Conversely, plans expressed in symbols must be translated into signals for the muscles. Without a mapping to images, the symbols manipulated in programs (or the brain) would form meaningless syntactic structures with no semantic interpretation. Perception is the process of classifying continuous images in discrete categories. The perception of an object is a kind of abductive reasoning on the basis of incomplete evidence, as Peirce was well aware (CP 5.181):
Abductive inference shades into perceptual judgment without any sharp line of demarcation between them; or in other words, our first premises, the perceptual judgments, are to be regarded as an extreme case of abductive inferences, from which they differ in being absolutely beyond criticism. The abductive suggestion comes to us like a flash. It is an act of insight, although of extremely fallible insight. It is true that the different elements of the hypothesis were in our minds before; but it is the idea of putting together what we had never before dreamed of putting together which flashes the new suggestion before our contemplation.Peirce explicitly stated the form of the perceptual abduction in his review of William James's Principles of Psychology:
This is the kind of inference that takes place automatically in every act of perception. The brain is a highly efficient abductive reasoner, and only an imperfect deductive reasoner.A well-recognized kind of object M has for its ordinary predicates P1, P2, P3, etc., indistinctly recognized. The suggesting object S has these same predicates P1, P2, P3, etc. Hence, S is of the kind M.
Although deduction is not the brain's primary reasoning process, it is valuable for its precision in extended chains of reasoning. Logic is good for precise reasoning about discrete structures, but iconic simulations are better for reasoning about continuity. Yet the two processes can be closely related. As in the example in Section 1, a continuous model may be constructed from instructions stated as propositions, and measurements of its dimensions, areas, and volume may be expressed in propositions. To relate the continuous and the discrete, the following theory of symbol grounding was presented in Conceptual Structures (Sowa 1984):
The brain is primarily an abductive reasoner that is well suited to processing continuous images; discrete symbol processing is built on top of the underlying continuous system. Conventional AI systems, by contrast, are primarily deductive reasoners that are best suited to processing discrete symbols; they can only approximate continuous systems by combinations of discrete elements. The need for both kinds of processes is not a consequence of psychological studies or AI simulations. Instead, it results from the structure of logic and the structure of the world: continuous models are necessary to represent the world because that is the way the world works; discrete symbols are necessary for deduction because that is the way logic works.
In his later philosophy, Wittgenstein was trying to address the problems of the richness, complexity, and unresolvable inconsistencies in the knowledge soup. His solution was to abandon the search for a single consistent semantics for all of language and knowledge and to propose his theory of language games: language is not a monolithic system, but a collection of games, each specialized for a different domain and a different purpose. This view has major implications for future developments in AI:
Statistics is important for determining the salience of chunks in the soup and selecting the most promising ones for an application. Logic is needed to check their relevance and to do inferences from them. Even the scruffy heuristics have a place: frames, scripts, MOPs, and TOPs are possible ways of organizing the knowledge in the soup (provided, of course, that they are defined precisely enough to be compatible with the logic-based methods). Case-baed reasoning (Kolodner 1988) is a good example of how nonformalized background knowledge can be adapted to form an incipient theory about new circumstances. The theory of knowledge soup makes room for everybody: there is a need for logic in deduction and a need for heuristics and connectionism in abduction. Both the scruffies and the neats can contribute to the approach, and people in both camps can take advantage of each other's strengths.
This article evolved from lectures of the same title that I presented at various places since 1987. During that time, I have spoken with or corresponded with a number of people about these issues. I would like to acknowledge helpful comments from Charley Bontempo, Ed Feigenbaum, Norman Foo, Peter Gärdenfors, Isaac Levi, Ron Loui, Paula Newman, Donald Norman, Anand Rao, Doug Skuce, and Wlodek Zadrozny. I must also thank Maria Zemankova for prodding me into converting my lectures into written form.
Alchourron, C., P. Gärdenfors, & D. Mackinson (1985) "On the theory of change: partial meet contraction and revision functions," J. of Symbolic Logic 50:2, 510-530.
Brachman, R. J. (1985) ""I lied about the trees," Or defaults and definitions in knowledge representation," AI Magazine 6:3, 80-93.
Chapman, D. (1989) "Penguins can make cake," AI Magazine 10:4, 45-50.
Craik, K. J. W. (1952) The Nature of Explanation, Cambridge University Press, Cambridge.
Finke, R. A. (1989) Principles of Mental Imagery, MIT Press, Cambridge, MA.
Gärdenfors, P. (1988) Knowledge in Flux: Modeling the Dynamics of Epistemic States, MIT Press, Cambridge, MA.
Gärdenfors, P., & D. Mackinson (1988) "Revision of knowledge systems using epistemic entrenchment," Proc. of Conf. on Theoretical Aspects of Reasoning about Knowledge, Almaden.
Ginsberg, M. L., ed. (1987) Readings in Nonmonotonic Reasoning, Morgan Kaufmann Publishers, San Mateo, CA.
Ginsberg, M. L. (1989a) "Universal planning: an (almost) universally bad idea," AI Magazine 10:4, 40-44.
Ginsberg, M. L. (1989b) "Universal planning research: a good or bad idea?," AI Magazine 10:4, 61-62.
Harnad, S. (1990) "The symbol grounding problem," Physica D, in press.
Israel, D. J. (1980) "What's wrong with nonmonotonic logic?" Proc. AAAI-80, 99-101.
Kolodner, J., ed. (1988) Proc. Case-Based Reasoning Workshop, DARPA.
Levi, Isaac (1980) The Enterprise of Knowledge, MIT Press, Cambridge, MA.
Levesque, H. J. (1989) "A knowledge-level account of abduction," Proc. IJCAI-89, 1061-1067.
McCarthy, J. (1980) "Circumscription — a form of nonmonotonic reasoning," Artificial Intelligence 13, 27-39, 171-172.
McDermott, D. V. (1987) "A critique of pure reason," Computational Intelligence 3, 151-160.
Minsky, M. (1965) "Matter, mind and models," Proc. IFIP Congress 65, pp. 45-49.
Minsky, M. (1975) "A framework for representing knowledge," in P. Winston, ed., The Psychology of Computer Vision, McGraw-Hill, New York, 211-280.
Neisser, U. (1967) Cognitive Psychology, Appleton Century Crofts, New York.
Pearl, J. (1988) Probabilistic Reasoning in Intelligent Systems, Morgan Kaufmann Publishers, San Mateo, CA.
Peirce, C. S. (1931-1958) Collected Papers of C. S. Peirce, ed. by C. Hartshorne, P. Weiss, & A. Burks, 8 vols., Cambridge, MA.
Peirce, C. S. (1891) "Review of Principles of Psychology by William James," Nation 53, p. 32.
Poole, D. (1989) "Normality and faults in logic-based diagnosis," Proc. IJCAI-89, 1304-1310.
Pople, H. E., J. D. Myers, & R. A. Miller (1975) "DIALOG: a model of diagnostic logic for internal medicine," Proc. IJCAI-75, 848-855.
Pople, H. (1982) "Heuristic methods for imposing structure on ill-structured problems," in P. Szolovits, ed., Artificial Intelligence in Medicine, Westview Press, Boulder.
Rao, A. S. & N. Y. Foo (1989a) "Formal theories of belief revision," Proc. of the First International Conference on Principles of Knowledge Representation and Reasoning, Morgan Kaufmann Publishers, San Mateo, CA, 369-380.
Rao, A. S., & N. Y. Foo (1989b) "Minimal change and maximal coherence: a basis for belief revision and reasoning about actions," Proc. IJCAI-89.
Reggia, J. A., D. S. Nau, & P. Y. Wang (1983) "Diagnostic expert systems based on a set covering model," Int. J. Man-Machine Studies 19:5, 437-460.
Reiter, R. (1980) "A logic for default reasoning," Artificial Intelligence 13, 81-132.
Reiter, R., & G. Criscuolo (1981) "On interacting defaults," Proc. IJCAI-81, 270-276.
Schank, R. C., & R. Abelson (1977) Scripts, Plans, Goals, and Understanding, Erlbaum, Hillsdale, NJ.
Schank, R. C. (1982) Dynamic Memory, Cambridge University Press.
Schoppers, M. J. (1987) "Universal plans for reactive robots in unpredictable environments," Proc. IJCAI-87, 852-859.
Schoppers, M. J. (1989) "In defense of reaction plans as caches," AI Magazine 10:4, 51-60.
Smith, B. C. (1982) "Prolog to Reflections and Semantics in a Procedural Language," reprinted in R. J. Brachman & H. J. Levesque, eds., Readings in Knowledge Representation, Morgan Kaufmann Publishers, San Mateo, CA, 31-39.
Sowa, J. F. (1984) Conceptual Structures: Information Processing in Mind and Machine, Addison-Wesley, Reading, MA.
Sowa, J. F., ed. (1990) Principles of Semantic Networks, Morgan Kaufmann Publishers, forthcoming.
Thomason, R. H., & D. S. Touretzky (1990) "Inheritance Theory and Relational Networks," to appear in Sowa (1990).
Twine, S. (1990) "Representing facts in KEE's frame language," Artificial Intelligence in Databases and Information Systems, edited by R. A. Meersman, Zh. Shi, & C-H Kung, North-Holland, Amsterdam, 355-398.
Waismann, F. (1952) "Verifiability," in A. Flew, ed., Logic and Language, first series, Basil Blackwell, Oxford.
Wittgenstein, L. (1953) Philosophical Investigations, Basil Blackwell, Oxford.
Zadeh, L. A. (1974) "Fuzzy logic and its application to approximate reasoning," Information Processing 74, North-Holland, Amsterdam, 591-594.
Zadrozny, W., & M. M. Kokar (1990) "A logical model of machine learning: A study of vague predicates," in P. Benjamin, ed., Change of Representation and Inductive Bias, Kluwer, in press.
Zadrozny, W. (forthcoming) "The logic of abduction," IBM Research, Yorktown Heights, NY.
Last Modified: