
Figure 1: A fan for the word bank
Abstract. Natural languages are easy to learn by infants, they can express any thought that any adult might ever conceive, and they accommodate the limitations of human breathing rates and short-term memory. The first property implies a finite vocabulary, the second implies infinite extensibility, and the third implies a small upper bound on the length of phrases. Together, they imply that most words in a natural language will have an open-ended number of senses — ambiguity is inevitable. Peirce and Wittgenstein are two philosophers who understood that vagueness and ambiguity are not defects in language, but essential properties that enable it to accommodate anything and everything that people need to say. In analyzing the ambiguities, Wittgenstein developed his theory of language games, which allow words to have different senses in different contexts, applications, or modes of use. Recent developments in lexical semantics, which are remarkably compatible with the views of Peirce and Wittgenstein, are based on the recognition that words have an open-ended number of dynamically changing and context-dependent microsenses. The resulting flexibility enables natural languages to adapt to any possible subject from any perspective for any humanly conceivable purpose. To achieve a comparable level of flexibility with formal ontologies, this paper proposes an organization with a dynamically evolving collection of formal theories, systematic mappings to formal concept types and informal lexicons of natural language terms, and a modularity that allows independent distributed development and extension of all resources, formal and informal.
Published in Formal Ontology in Information Systems, edited by B. Bennett & C. Fellbaum, IOS Press, Amsterdam, 2006.
Formal languages, such as logic and computer programs, are precise, but what they express so precisely may have no relationship to what the author intended. Even when the author or programmer has corrected all the bugs or obvious discrepancies, the result might not satisfy the users' requirements. Engineers summarize the problem in a pithy slogan:
Customers never know what they want until they see what they get.More generally, the precision and clarity that are so admirable in the final specification of a successful system are the result of a lengthy process of discussion, analysis, and negotiation with many intermediate stages of trial, error, and revision. In most cases, the process of revision never ends until the system is obsolete, or as IBM euphemistically declares, "functionally stabilized." This predicament, which occurs in every area of science, engineering, business, and government, illustrates a universal principle: Precision and clarity are the goal, not the starting point of analysis, design, planning, or development. That principle has profound implications for ontology: A precise, finished ontology stated in a formal language is as unrealistic as a finished computer system.
Unlike formal languages, which can only express the finished result of a lengthy analysis, natural languages can express every step from an initially vague idea to the final specification. During his career as an experimental physicist and a practicing engineer, Peirce learned the difficulty of stating any general principle with absolute precision:
It is easy to speak with precision upon a general theme. Only, one must commonly surrender all ambition to be certain. It is equally easy to be certain. One has only to be sufficiently vague. It is not so difficult to be pretty precise and fairly certain at once about a very narrow subject. (CP 4.237)This quotation summarizes the futility of any attempt to develop a precisely defined ontology of everything, but it offers two useful alternatives: an informal classification, such as a thesaurus or terminology designed for human readers; and an open-ended collection of formal theories about narrowly delimited subjects. It also raises the questions of how and whether the informal resources might be used as a bridge between informal natural language and formally defined logics and programming languages.
In his first book, Wittgenstein (1921) restricted the legitimate uses of language to precisely defined mappings from sentences to configurations of objects in the world. But later, Wittgenstein (1953) faced the full complexity of language as it is used in science and everyday life. For his theory of language games, he observed that words do not have a fixed boundary defined by necessary and sufficient conditions. As an alternative, he suggested the term family resemblances for the "complicated network of overlapping and criss-crossing similarities, in the large and the small" (§66), and he did not consider vagueness a defect:
One might say that the concept 'game' is a concept with blurred edges. — "But is a blurred concept a concept at all?" — Is an indistinct photograph a picture of a person at all? Is it even always an advantage to replace an indistinct picture with a sharp one? Isn't the indistinct one often exactly what we need?Frege's view is incompatible with natural languages and with every branch of empirical science and engineering. With their background in engineering, Peirce and Wittgenstein recognized that all measurements have a margin of error or granularity, which must be taken into account at every step from design to implementation. The option of vagueness enables language to accommodate the inevitable vagueness in observations and the plans that are based on them.Frege compares a concept to an area and says that an area with vague boundaries cannot be called an area at all. This presumably means that we cannot do anything with it. — But is it senseless to say: "Stand roughly (ungefähr) there"? (§71).
This paper takes these insights as inspiration for a dynamic theory of ontology, which relates the variable meanings of a finite set of words to a potentially infinite set of concept and relation types, which are used and reused in a dynamically evolving lattice of theories. Section 2 reviews related research in natural language semantics and some pioneering efforts in computational linguistics by Margaret Masterman, a former student of Wittgenstein's. To relate language to formal theories, Section 3 relates words to concept types to canonical graphs and then to a lattice of theories. Section 4 shows how that lattice can be used in both formal and informal reasoning. The concluding Section 5 discusses the implications of this approach on the design of ontologies and the interfaces to their users and developers.
During the second half of the 20th century, various models of language understanding were proposed and implemented in computer programs. All of them have been useful for processing some aspects of language, but none of them have been adequate for all aspects of language or even for full coverage of just a single aspect:
A novel version of lexical semantics, influenced by Wittgenstein's language games and related developments in cognitive science, is the theory of dynamic construal of meaning (DCM) proposed by Cruse (2000) and developed further by Croft and Cruse (2004). The fundamental assumption of DCM is that the most stable aspect of a word is its spoken or written sign; its meaning is unstable and dynamically evolving as it is construed in each context in which it is used. Cruse coined the term microsense for each subtle variation in meaning as a word is used in different language games. That is an independent rediscovery of Peirce's view: sign types are stable, but the interpretations of a sign token in different contexts have no direct relationship to one another. The interpretation by each mind depends on the sign itself and its immediate context in a pattern of other signs, the physical environment, and each mind's memory of previous patterns of signs. Croft and Cruse showed how the DCM view of semantics could be integrated with a version of construction grammar, but their descriptions are not sufficiently detailed to be implemented in a computer system.
A model of language directly inspired by Wittgenstein's language games was developed by Margaret Masterman, one of six students in his course of 1933-34 whose notes were compiled as The Blue Book. In the late 1950s, Masterman founded the Cambridge Language Research Unit (CLRU) as a discussion group, which became one of the pioneering centers of research in computational linguistics. Her collected papers from the late 1950s to 1980 (Masterman 2005) present a computable version with many similarities to DCM:

Figure 1: A fan for the word bank
To illustrate the use of fans, Masterman analyzed the phrases up the steep bank and in the savings bank. All the words except the would have similar fans, and her algorithm would "pare down" the ambiguities "by retaining only the spokes that retain ideas which occur in each." For this example, it would retain "OBLIQUITY 220 in 'steep' and 'bank'; whereas it retains as common between 'savings' and 'bank' both of the two areas STORE 632 and TREASURY 799." She went on to discuss methods of handling various exceptions and complications, but all the algorithms use only words and families of words that actually occur in English. They never use abstract or artificial markers, features, or categories. That approach suggests a plausible cognitive theory: From an infant's first words to an adult's level of competence, language learning is a continuous process of building and refining the stock of words, families of words grouped by their use in common situations, and patterns of connections among the words and families.
Wittgenstein's language games and the related proposals by Cruse, Croft, and Masterman are more realistic models of natural language than the rigid theories of formal semantics. Yet scientists, engineers, and computer programmers routinely produce highly precise language-like structures by disciplined extensions of the methods used for ordinary language. A complete theory of language must be able to explain every level of competence from the initial vague stages to the most highly disciplined reasoning and representations of science. Furthermore, the level of precision needed to write computer programs can be acquired by school children without formal training. There is no linguistic or psychological evidence for a discontinuity in the methods of language production and interpretation.
In order to handle both formal and informal language, Masterman's approach must be extended with links to logic, but in a way that permits arbitrary revisions. Figure 2 illustrates a word fan that maps words to concept types to canonical graphs and finally to a lattice of theories. In this paper, the canonical graphs are represented as conceptual graphs (CGs), a formally defined version of logic that has the same model-theoretic foundation as Common Logic (ISO/IEC 2006). Equivalent operations may be performed with any notation, but examples shown as graphs are easier to read. No formal logic can be vague, but the axioms of a theory may be underspecified to accommodate multiple options in the subtheories. When precision is necessary, any theory may be specialized in order to tighten the constraints and add any required detail.
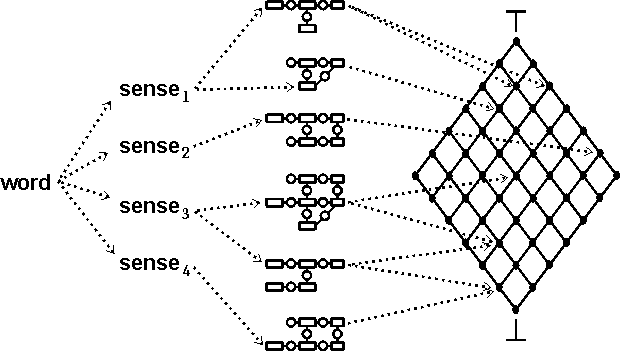
Figure 2: words → types → canonical graphs → lattice of theories
The fan on the left of Figure 2 links each word to an open-ended list of concept types, each of which corresponds to some area of a thesaurus in Masterman's system. The word bank, for example, could be linked to types with labels such as Bank799 or Bank_Treasury. In various applications or language games, those types could be further subdivided into finer grained subtypes, which would correspond to Cruse's microsenses. The selection of subtypes is determined by canonical graphs, which specify the characteristic patterns of concepts and relations associated with each type or subtype. Figure 3 illustrates three canonical graphs for the types Give, Easy, and Eager.

Figure 3: Canonical graphs for the types Give, Easy, and Eager
A canonical graph for a type is a conceptual graph that specifies one of the patterns characteristic of that type. On the left, the canonical graph for Give represents the same constraints as a typical case frame for a verb. It states that the agent (Agnt) must be Animate, the recipient (Rcpt) must be Animate, and the object (Obj) may be any Entity. The canonical graphs for Easy and Eager, however, illustrate the advantage of graphs over frames: a graph permits cycles, and the arcs can distinguish the directionality of the relations. Consider the following two sentences:
Bob is easy to please. Bob is eager to please.For both sentences, the concept [Person: Bob] would be linked via the attribute relation (Attr) to the concept [Easy] or [Eager], and the act [Please] would be linked via the manner relation (Manr) to the same concept. But the canonical graph for Easy would make Bob the object of the act Please, and the graph for Eager would make Bob the agent. The first sentence below is acceptable because the object may be any entity, but the constraint that the agent of an act must be animate would make the second sentence unacceptable:
The book is easy to read. * The book is eager to read.Chomsky (1965) used the easy/eager example to argue for different syntactic transformations associated with the two adjectives. But the canonical graphs state semantic constraints that cover a wider range of linguistic phenomena with simpler syntactic rules. A child learning a first language or an adult reading a foreign language can use semantic constraints to interpret sentences with unknown or even ungrammatical syntax. Under Chomsky's hypothesis that syntax is a prerequisite for semantics, such learning is inexplicable.
Canonical graphs with a few concept nodes are adequate to discriminate the general senses of most words, but the canonical graphs for detailed microsenses can become much more complex. For the adjective easy, the microsenses occur in very different patterns for a book that's easy to read, a person that's easy to please, or a car that's easy to drive. For the verb give, a large dictionary lists dozens of senses, and the number of microsenses is enormous. The prototypical act of giving is to hand something to someone, but a large object can be given just by pointing to it and saying "It's yours." When the gift is an action, as in giving a kiss, a kick, or a bath, the canonical graph used to parse the sentence has a few more nodes. But the graphs required to understand the implications of each type of action are far more complex, and they're related to the graphs for taking a bath or stealing a kiss.
The canonical graph for buy typically has two acts of giving: money from the buyer to the seller, and some goods from the seller to the buyer. But the canonical graphs needed to understand various microsenses may require far more detail about the buyers, the sellers, the goods sold, and other people, places, and things involved. Buying a computer, for example, can be done by clicking some boxes on a screen and typing the billing and shipping information. That process may trigger a series of international transactions, which can be viewed by going to the UPS web site to check when the computer was airmailed from Hong Kong and delivered to New York. All that detail is involved in one microsense of the verb buy. In a successful transaction, the buyer can ignore most of it, but somebody must be able to trace the steps if something goes wrong.
An important purpose of the lattice of theories is to facilitate modularity and to allow independent agents (human or computer) to revise arbitrary aspects of the knowledge at any level of detail. The theories in the lattice may be large or small, and they may be stated in any version of logic, but CL is assumed for this paper. The position of each theory in the lattice shows how it is related to every other theory. If theory x is above theory y, then x is more general than y, and y is more specialized than x. If theory x is neither above nor below y, then they are siblings or cousins. New theories can be added at the top, bottom, or middle levels of the lattice at any time without affecting any application that uses other theories. The complete lattice of all possible theories is infinite, but only a finite subset is ever implemented in an actual system.
A lattice of first-order theories combined with metalevel reasoning for selecting a theory is a powerful technique that avoids multiplicities of special-purpose logics. Instead of nonmonotonic logics, belief revision can be treated as a metalevel walk through the lattice to select an appropriate revision of the current theory (Sowa 2000). Instead of multiple logics for every modality, metalevel reasoning about the selection of laws (axioms) provides a foundation for multimodal reasoning that subsumes the semantics of Kripke, Montague, and many others as special cases (Sowa 2003, 2006). Instead of special-purpose logics of ambiguity (van Deemter & Peters 1996), this paper proposes metalevel reasoning about the lattice as a way of simulating Wittgenstein's language games.
Formal and informal reasoning should not be considered incompatible or conflicting. Instead, formal reasoning is a more disciplined application of the techniques used for informal reasoning. Analogy, the process of finding common patterns in different structures, is the foundation for both. The logical methods of reasoning by induction, deduction, and abduction are distinguished by the constraints they impose on analogy. Following is a summary of the structure-mapping operations that occur at each step of formal logic (Sowa & Majumdar 2003):
Deduction can never introduce anything new that is not already implicit in a given theory. In terms of the lattice, deduction stays within the bounds of a single theory. Methods of theory revision move from one theory to another by deleting, adding, or modifying axioms Figure 4 shows the four basic operators for navigating the lattice: contraction, expansion, revision, and analogy (Sowa 2000). The operators of contraction and expansion follow the arcs of the lattice, revision makes short hops sideways, and analogy makes long-distance jumps.
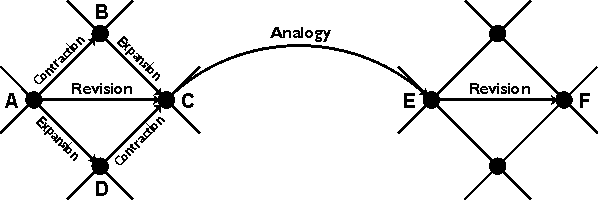
Figure 4: Four operators for navigating the lattice of theories
To illustrate the moves through the lattice, suppose that A is Newton's theory of gravitation applied to the earth revolving around the sun and F is Niels Bohr's theory about an electron revolving around the nucleus of a hydrogen atom. The path from A to F is a step-by-step transformation of the old theory to the new one. The revision step from A to C replaces the gravitational attraction between the earth and the sun with the electrical attraction between the electron and the proton. That step can be carried out in two intermediate steps:
The lattice of theories can be viewed as the theoretical background for a wide range of developments in AI, ranging from informal heuristics to the most sophisticated methods of learning and reasoning. In fact, any method of default or nonmonotonic reasoning can be interpreted as a strategy for walking and jumping through the infinite lattice in search of a suitable theory. For vague or incomplete theories, a theorem prover can be used to check consistency. If no contradictions are found, they can be placed in the lattice, and the methods of theory revision can be used to refine and extend them to a more complete version for their intended application. Mappings specified according to Figure 2 can be used to relate any aspect of any theory in the lattice to natural language statements or queries.
The lattice of theories presented in Sections 3 and 4 is neutral with respect to global consistency. It does not rule out the possibility that there might exist one ideal theory of everything that could be used at every level from top to bottom, but there is no evidence that global consistency is necessary or even desirable for all applications. On the contrary, no branch of science or engineering has a globally consistent set of axioms. For the Cyc system (Lenat 1995), the largest formal ontology ever developed, the axioms are subdivided among several thousand microtheories with no requirement for consistency among them. Although Cyc has a single top-level ontology, Lenat has said that the axioms at the middle levels are generally more useful and that the axioms at the lowest, task-oriented levels are the most relevant for specific problems.
The evidence from natural language use and from engineering design and development indicates that a bottom-up, task-oriented approach is the way children learn language, adults use language, and scientists and engineers develop their theories and designs. In short, Wittgenstein's later theory with a multiplicity of language games is a more realistic model for language than his early unified theory of a single fixed mapping from language to the world.
The implications for ontology are significant: Low-level, task-oriented modules have been the most successful in science, engineering, business, and everyday life. The largest ontology project ever attempted began with a globally consistent set of axioms, but later divided it into a multiplicity of independently developed microtheories. That evidence does not prove that global consistency is impossible, but it suggests that a modular approach is easier to implement. A lattice of theories can accommodate both. It permits the development of independent modules, but it includes all possible generalizations and combinations. The recommended strategy is to support modularity, provide the lattice operators for theory revision, and allow whatever consensus is appropriate to evolve from the bottom up.
Chomsky, Noam (1965) Aspects of the Theory of Syntax, MIT Press, Cambridge, MA.
Croft, William, & D. Alan Cruse (2004) Cognitive linguistics, Cambridge University Press, Cambridge, MA.
Cruse, D. Alan (2000) "Aspects of the micro-structure of word meanings," in Y. Ravin & C. Leacock, eds. (2000) Polysemy: Theoretical and Computational Approaches, Oxford University Press, Oxford, pp. 30-51.
ISO/IEC (2006) Common Logic: A Framework for a Family of Logic-Based Languages, Final Committee Draft, available at http://cl.tamu.edu .
Lenat, Douglas B. (1995) "Cyc: A large-scale investment in knowledge infrastructure," Communications of the ACM 38:11, 33-38.
Masterman, Margaret (2005) Language, Cohesion and Form, edited by Yorick Wilks, Cambridge University Press, Cambridge.
Peirce, Charles Sanders (CP) Collected Papers of C. S. Peirce, ed. by C. Hartshorne, P. Weiss, & A. Burks, 8 vols., Harvard University Press, Cambridge, MA, 1931-1958.
Sowa, John F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole Publishing Co., Pacific Grove, CA.
Sowa, John F. (2003) "Laws, facts, and contexts: Foundations for multimodal reasoning," in Knowledge Contributors, edited by V. F. Hendricks, K. F. Jørgensen, and S. A. Pedersen, Kluwer Academic Publishers, Dordrecht, pp. 145-184. http://www.jfsowa.com/pubs/laws.htm
Sowa, John F. (2006) "Worlds, Models, and Descriptions," Studia Logica, Special Issue Ways of Worlds II, to appear in November.
Sowa, John F., & Arun K. Majumdar (2003) "Analogical reasoning," in A. de Moor, W. Lex, & B. Ganter, eds., Conceptual Structures for Knowledge Creation and Communication, LNAI 2746, Springer-Verlag, Berlin, pp. 16-36. http://www.jfsowa.com/pubs/analog.htm
van Deemter, Kees, & Stanley Peters (1996) Semantic Ambiguity and Underspecification, CSLI, Stanford, CA.
Wittgenstein, Ludwig (1921) Tractatus Logico-Philosophicus, Routledge & Kegan Paul, London.
Wittgenstein, Ludwig (1953) Philosophical Investigations, Basil Blackwell, Oxford.