Laws, Facts, and Contexts:
Foundations for Multimodal Reasoning

Abstract.  Leibniz's intuition that necessity corresponds to truth in all possible worlds enabled Kripke to define a rigorous model theory for several axiomatizations of modal logic. Unfortunately, Kripke's model structures lead to a combinatorial explosion when they are extended to all the varieties of modality and intentionality that people routinely use in ordinary language. As an alternative, any semantics based on possible worlds can be replaced by a simpler and more easily generalizable approach based on Dunn's semantics of laws and facts and a theory of contexts based on the ideas of Peirce and McCarthy. To demonstrate consistency, this article defines a family of nested graph models, which can be specialized to a wide variety of model structures, including Kripke's models, situation semantics, temporal models, and many variations of them. An important advantage of nested graph models is the option of partitioning the reasoning tasks into separate metalevel stages, each of which can be axiomatized in classical first-order logic. At each stage, all inferences can be carried out with well-understood theorem provers for FOL or some subset of FOL. To prove that nothing more than FOL is required, Section 6 shows how any nested graph model with a finite nesting depth can be flattened to a conventional Tarski-style model. For most purposes, however, the nested models are computationally more tractable and intuitively more understandable.

An earlier version of this article was presented at the Φlog Conference in Denmark in May 2002. This version has been published in Knowledge Contributors, edited by V. F. Hendricks, K. F. Jørgensen, and S. A. Pedersen, Kluwer Academic Publishers, Dordrecht, 2003, pp. 145-184.

1. Replacing Possible Worlds with Contexts

Possible worlds have been the most popular semantic foundation for modal logic since Kripke (1963) adopted them for his version of model structures. Lewis (1986), for example, argued that "We ought to believe in other possible worlds and individuals because systematic philosophy goes more smoothly in many ways if we do." Yet computer implementations of modal reasoning replace possible worlds with "ersatz worlds" consisting of collections of propositions that more closely resemble Hintikka's (1963) model sets. By dividing the model sets into necessary laws and contingent facts, Dunn (1973) defined a conservative refinement of Kripke's semantics that eliminated the need for a "realist" view of possible worlds. Instead of assuming Kripke's accessibility relation as an unexplained primitive, Dunn derived it from the selection of laws and facts.

Since Dunn's semantics is logically equivalent to Kripke's for conventional modalities, most logicians ignored it in favor of Kripke's. For multimodal reasoning, however, Dunn's approach simplifies the reasoning process by separating the metalevel reasoning about laws and facts from the object-level reasoning in ordinary first-order logic. For each modality, Kripke semantics supports two operators such as for necessity and ◊ for possibility. For temporal logic, the same two operators are interpreted as always and sometimes. For deontic logic, they are reinterpreted as obligation and permission. That approach cannot represent, much less reason about a sentence that mixes all three modalities, such as You are never obligated to do anything impossible. The limitation to just one modality is what Scott (1970) considered "one of the biggest mistakes of all in modal logic":

The only way to have any philosophically significant results in deontic or epistemic logic is to combine these operators with:  Tense operators (otherwise how can you formulate principles of change?); the logical operators (otherwise how can you compare the relative with the absolute?); the operators like historical or physical necessity (otherwise how can you relate the agent to his environment?); and so on and so on. (p. 143)

To take advantage of Dunn's semantics, the metalevel reasoning should be performed in a separate context from the object-level reasoning. This separation requires a formal theory of contexts that can distinguish different metalevels. But as Rich Thomason (2001) observed, "The theory of context is important and problematic — problematic because the intuitions are confused, because disparate disciplines are involved, and because the chronic problem in cognitive science of how to arrive at a productive relation between formalizations and applications applies with particular force to this area." The version of contexts adopted for this article is based on a representation that Peirce introduced for existential graphs (EGs) and Sowa (1984) adopted as a foundation for conceptual graphs (CGs). That approach is further elaborated along the lines suggested by McCarthy (1993) and developed by Sowa (1995, 2000).

Sections 2, 3, and 4 of this article summarize Dunn's semantics of laws and facts, a theory of contexts based on the work of Peirce and McCarthy, and Tarski's hierarchy of metalevels. Then Section 5 introduces nested graph models (NGMs) as a general formalism for a family of models that can be specialized for various theories of modality and intentionality. Section 6 shows how any NGM with a finite depth of nesting can be flattened to a Tarski-style model consisting of nothing but a set D of individuals and a set R of relations over D. Although the process of flattening shows that modalities can be represented in first-order logic, the flattening comes at the expense of adding extra arguments to each relation to indicate every context in which it is nested. Finally, Section 7 shows how Peirce's semeiotic, Dunn's semantics, Tarski's metalevels, and nested graph models provide a powerful combination of tools for analyzing and formalizing semantic relationships.

2. Dunn's Laws and Facts

Philosophers since Aristotle have recognized that modality is related to laws; Dunn's innovation made the relationships explicit. Instead of Kripke's primitive accessibility relation between worlds, Dunn (1973) replaced each possible world with two sets of propositions called laws and facts. For every Kripke world w, Dunn assumed an ordered pair (M,L), where M is a Hintikka-style model set called the facts of w and L is a subset of M called the laws of w. For this article, the following conventions are assumed:

• Axioms.  Any subset A of L whose deductive closure is the laws (A |− L) is called an axiom set for (M,L).

• Facts.  The set of all facts M is maximally consistent:  for any proposition p, either p∈M or ~p∈M, but not both.

• Contingent facts.  The set M−L of all facts that are not laws is called the contingent facts.

• Closure.  The facts are the deductive closure of any axiom set A and the contingent facts: 
  A ∪ (M − L) |− M.

To show how the accessibility relation from one world to another can be derived from the choice of laws, let (M₁,L₁) be a pair of facts and laws that describe a possible world w₁, and let the pair (M₂,L₂) describe a world w₂. Dunn defined accessibility from the world w₁ to the world w₂ to mean that the laws L₁ are a subset of the facts in M₂:

R(w₁,w₂) ≡ L₁⊂M₂.

◊p ≡ (∃w:World)(R(w₀,w) ∧ w|=p).

◊p ≡ (∃M:ModelSet) (L₀ ⊂M ∧ p∈M).

p ≡ (∀M:ModelSet)(L₀ ⊂M ⊃ p∈M).

Dunn performed the same substitutions in Kripke's constraints on the accessibility relation. The result is a restatement of the constraints in terms of the laws and facts:

• System T.  The two axioms p⊃p and p⊃◊p require every world to be accessible from itself. That property follows from Dunn's definition because the laws L of any world are a subset of the facts:  L⊂M.

• System S4.  System T with axiom S4, p⊃p, requires that R must also be transitive. It imposes the tighter constraint that the laws of the first world must be a subset of the laws of the second world: L₁⊂L₂.

• System S5.  System S4 with axiom S5, ◊p⊃◊p, requires that R must also be symmetric. It constrains both worlds to have exactly the same laws:  L₁=L₂.

Dunn's theory is a conservative refinement of Kripke's theory, since any Kripke model structure (K,R,Φ) can be converted to one of Dunn's model structures in two steps:

1. Replace every world w in K with the set M of propositions that are true in w and the set L of propositions that are necessary in w.

   M = {p | Φ(p,w) = true}.

   L = {p | (∀u:World)(R(w,u) ⊃ Φ(p,u) = true}.

2. Define Kripke's primitive accessibility relation R(u,v) by the constraint that the laws of u are true in v:

   R(u,v) ≡ (∀p:Proposition)(p∈L_u ⊃ p∈M_v).

Every axiom and theorem of Kripke's theory remains true in Dunn's version, but Dunn's theory makes the reasons for modality available for further inferences. For theories of intentionality, Dunn's approach can relate the laws to the goals and purposes of some agent, who in effect legislates which propositions are to be considered laws. This approach formalizes an informal suggestion by Hughes and Cresswell (1968):  "a world, w₂, is accessible to a world, w₁, if w₂ is conceivable by someone living in w₁." In Dunn's terms, the laws that determine what is necessary in the world w₁ are the propositions that are not conceivably false for someone living in w₁.

3. Contexts by Peirce and McCarthy

In first-order logic, laws and facts are propositions, and there is no special mark that distinguishes a law from a fact. To distinguish them, a context mechanism is necessary to separate first-order reasoning with the propositions from metalevel reasoning about the propositions and about the distinctions between laws and facts. Peirce (1880, 1885) invented the algebraic notation for predicate calculus, which with a change of symbols by Peano became today's most widely used notation for logic. A dozen years later, Peirce developed a graphical notation for logic that more clearly distinguishes contexts. Figure 1 shows his graph notation for delimiting the context of a proposition. In explaining that graph, Peirce (1898) said "When we wish to assert something about a proposition without asserting the proposition itself, we will enclose it in a lightly drawn oval." The line attached to the oval links it to a relation that makes a metalevel assertion about the nested proposition.

Figure 1:  One of Peirce's graphs for talking about a proposition

The oval serves the syntactic function of grouping related information in a package. Besides notation, Peirce developed a theory of the semantics and pragmatics of contexts and the rules of inference for importing and exporting information into and out of contexts. To support first-order logic, the only metalevel relation required is negation. By combining negation with the existential-conjunctive subset of logic, Peirce developed his existential graphs (EGs), which are based on three logical operators and an open-ended number of relations:

1. Existential quantifier:  A bar or linked structure of bars, called a line of identity, represents ∃.

2. Conjunction:  The juxtaposition of two graphs in the same context represents ∧.

3. Negation:  An oval enclosure with no lines attached to it represents ~ or the denial of the enclosed proposition.

4. Relation:  Character strings represent the names of propositions, predicates, or relations, which may be attached to zero or more lines of identities.

Figure 2:  EG and CG for "If a farmer owns a donkey, then he beats it."

To illustrate the use of negative contexts for representing FOL, Figure 2 shows an existential graph and a conceptual graph for the sentence If a farmer owns a donkey, then he beats it. This sentence is one of a series of examples used by medieval logicians to illustrate issues in mapping language to logic. The EG on the left has two ovals with no attached lines; by default, they represent negations. It also has two lines of identity, represented as linked bars: one line, which connects farmer to the left side of owns and beats, represents an existentially quantified variable (∃x); the other line, which connects donkey to the right side of owns and beats represents another variable (∃y).

When the EG of Figure 2 is translated to predicate calculus, farmer and donkey map to monadic predicates; owns and beats map to dyadic predicates. If a relation is attached to more than one line of identity, the lines are ordered from left to right by their point of attachment to the name of the relation. With the implicit conjunctions represented by the ∧ symbol, the result is an untyped formula:

~(∃x)(∃y)(farmer(x) ∧ donkey(y) ∧ owns(x,y) ∧ ~beats(x,y)).

A nest of two ovals, as in Figure 2, is what Peirce called a scroll. It represents implication, since ~(p∧~q) is equivalent to p⊃q. Using the ⊃ symbol, the formula may be rewritten

(∀x)(∀y)((farmer(x) ∧ donkey(y) ∧ owns(x,y)) ⊃ beats(x,y)).

(∀x:Farmer)(∀y:Donkey)(owns(x,y) ⊃ beats(x,y)).

The nested graph models defined in Section 5 are based on the CG formalism, but with one restriction:  every graph must be wholly contained within a single context. The relation (Beats) in Figure 2 could not be linked to concept boxes outside its own context. To support that restriction, Figure 3 shows an equivalent CG in which concept boxes in different contexts are connected by dotted lines called coreference links, which indicate that the two concepts refer to exactly the same individual. A set of boxes connected by coreference links corresponds to what Peirce called a line of identity.

Figure 3:  A conceptual graph with coreference links

The symbol , which is a synonym for the type Entity, represents the most general type, which is true of everything. Therefore, concepts of the form [] correspond an unrestricted quantifier, such as (∃z). The dotted lines correspond to equations of the form x=z. Therefore, Figure 3 is equivalent to the following formula:

(∀x:Farmer)(∀y:Donkey)(owns(x,y) ⊃ (∃z)(∃w)(beats(z,w) ∧ x=z ∧ y=w)).

Besides attaching a relation to an oval, Peirce also used colors or tinctures to distinguish contexts other than negation. Figure 4 shows one of his examples with red (or shading) to indicate possibility. The graph contains four ovals:  the outer two form a scroll for if-then; the inner two represent possibility (shading) and impossibility (shading inside a negation). The outer oval may be read If there exist a person, a horse, and water; the next oval may be read then it is possible for the person to lead the horse to the water and not possible for the person to make the horse drink the water.

Figure 4:  EG for "You can lead a horse to water, but you can't make him drink."

The notation "—leads—to—" represents a triad or triadic relation leadsTo(x,y,z), and "—makes—drink—" represents makesDrink(x,y,z). In the algebraic notation with the symbol ◊ for possibility, Figure 4 maps to the following formula:

~(∃x)(∃y)(∃z)(person(x) ∧ horse(y) ∧ water(z) ∧ ~(◊leadsTo(x,y,z) ∧ ~◊makesDrink(x,y,z))).

(∀x)(∀y)(∀z)((person(x) ∧ horse(y) ∧ water(z)) ⊃ (◊leadsTo(x,y,z) ∧ ~◊makesDrink(x,y,z))).

Discourse representation theory.  The logician Hans Kamp once spent a summer translating English sentences from a scientific article to predicate calculus. During the course of his work, he was troubled by the same kinds of irregularities that puzzled the medieval logicians. In order to simplify the mapping from language to logic, Kamp (1981) developed discourse representation structures (DRSs) with an explicit notation for contexts. In terms of those structures, Kamp defined the rules of discourse representation theory for mapping quantifiers, determiners, and pronouns from language to logic (Kamp & Reyle 1993).

Although Kamp had not been aware of Peirce's existential graphs, his DRSs are structurally equivalent to Peirce's EGs. The diagram on the right of Figure 5 is a DRS for the donkey sentence, If there exist a farmer x and a donkey y and x owns y, then x beats y. The two boxes connected by an arrow represent an implication where the antecedent includes the consequent within its scope.

Figure 5:  EG and DRS for "If a farmer owns a donkey, then he beats it."

The DRS and EG notations look quite different, but they are exactly isomorphic:  they have the same primitives, the same scoping rules for variables or lines of identity, and the same translation to predicate calculus. Therefore, the EG and DRS notations map to the same formula:

~(∃x)(∃y)(farmer(x) ∧ donkey(y) ∧ owns(x,y) ∧ ~beats(x,y)).

McCarthy's contexts.  In his "Notes on Formalizing Context," McCarthy (1993) introduced the predicate ist(C,p), which may be read "the proposition p is true in context C." For clarity, it will be spelled out in the form isTrueIn(C, p). As illustrations, McCarthy gave the following examples:

• isTrueIn(contextOf("Sherlock Holmes stories"), "Holmes is a detective").

• isTrueIn(contextOf("U.S. legal history"), "Holmes is a Supreme Court Justice").

One of McCarthy's reasons for developing a theory of context was his uneasiness with the proliferation of new logics for every kind of modal, temporal, epistemic, and nonmonotonic reasoning. The ever-growing number of modes presented in AI journals and conferences is a throwback to the scholastic logicians who went beyond Aristotle's two modes necessary and possible to permissible, obligatory, doubtful, clear, generally known, heretical, said by the ancients, or written in Holy Scriptures. The medieval logicians spent so much time talking about modes that they were nicknamed the modistae. The modern logicians have axiomatized their modes and developed semantic models to support them, but each theory includes only one or two of the many modes. McCarthy (1977) observed,

For AI purposes, we would need all the above modal operators in the same system. This would make the semantic discussion of the resulting modal logic extremely complex.

• The facts of a context are determined by metalevel reasoning with the isTrueIn predicate:

  M = {p | isTrueIn(C,p)}.

• The laws of a context are determined by metalevel reasoning with the isLawOf predicate:

  L = {p | isLawOf(C,p)}.

4. Tarski's Metalevels

The semantics for multiple levels of nested contexts is based on the method of stratified metalevels by Tarski (1933). Each context in a nest is treated as a metalevel with respect to every context nested within it. The propositions in some context that has no nested levels beneath it may be considered as an object language L₀, which refers to entities in some universe of discourse D. The metalanguage L₁ refers to the symbols of L₀ and their relationships to D. Tarski showed that the metalanguage is still first order, but its universe of discourse is enlarged from D to L₀∪D. The metametalanguage L₂ is also first order, but its universe of discourse is L₁∪L₀∪D. To avoid paradoxes, Tarski insisted that no metalanguage L_n could refer to its own symbols, but it could refer to the symbols or individuals in the domain of any language L_i where 0≤i<n.

In short, metalevel reasoning is first-order reasoning about the way statements may be sorted into contexts. After the sorting has been done, reasoning with the propositions in a context can be handled by the usual FOL rules. At every level of the Tarski hierarchy of metalanguages, the reasoning process is governed by first-order rules. But first-order reasoning in language L_n has the effect of higher-order or modal reasoning for every language below n. At every level n, the model theory that justifies the reasoning in L_n is a conventional first-order Tarskian semantics, since the nature of the objects in the domain D_n is irrelevant to the rules that apply to L_n.

Example.  To illustrate the interplay of the metalevel and object-level inferences, consider the following statement, which includes direct quotation, indirect quotation, indexical pronouns, and metalanguage about belief:

Joe said "I don't believe in astrology, but everybody knows that it works even if you don't believe in it."

1. First mark the indexicals with the # symbol, and use square brackets to mark the multiple levels of nested contexts:

   Joe said
     [#I don't believe [in astrology]
       but everybody knows
         [[#it works]
           even if #you don't believe [in #it]]].
   

2. The indexical #I can be resolved to the speaker Joe, but the other indexicals depend on implicit background knowledge. The pronoun everybody is a universal quantifier that could be translated to "every person." The two occurrences of #it refer to astrology, but the three nested contexts about astrology have different forms; for simplicity, they could all be rewritten "astrology works." When no explicit person is being addressed, the indexical #you can be interpreted as a reference to any or every person who may be listening. For this example, it could be assumed to be coreferent with "every person" in the community. With these substitutions, the statement becomes

   Joe said
     [Joe doesn't believe [astrology works]
       but every person x knows
         [[astrology works]
           even if x doesn't believe
             [astrology works] ]].
   

3. If Joe's statement was sincere, Joe believes what he said. The word but could be replaced with the word and, which preserves the propositional content, but omits the contrastive emphasis. A statement of the form "p even if q" means that p is true independent of the truth value of q. It is equivalent to ((q⊃p) ∧ ((~q)⊃p)), which implies p by itself. The statement can therefore be rewritten

   Joe believes
     [Joe doesn't believe [astrology works]
       and every person x knows [astrology works] ].
   

4. Since Joe is a person in Joe's community, the constant "Joe" may be substituted for the quantifier "every person x":

   Joe believes
     [Joe doesn't believe [astrology works]
       and Joe knows [astrology works] ].
   

5. By the axioms of epistemic logic, everything known is believed. Therefore, the verb knows in third line can be replaced by the implicit believes:

   Joe believes
     [Joe doesn't believe [astrology works]
       and Joe believes [astrology works] ].
   

   This statement shows that Joe believes a contradiction of the form (~p ∧ p).

In the process of reasoning about Joe's beliefs, the context [astrology works] is treated as an encapsulated object, whose internal structure is ignored. When the levels interact, however, further axioms are necessary to relate them. Like the iterated modalities ◊◊p and ◊p, iterated beliefs occur in statements like Joe believes that Joe doesn't believe that astrology works. One reasonable axiom is that if an agent a believes that a believes p, then a believes p:

(∀a:Agent)(∀p:Proposition)(believe(a,believe(a,p)) ⊃ believe(a,p)).

5. Nested Graph Models

To prove that a syntactic notation for contexts is consistent, it is necessary to define a model-theoretic semantics for it. But to show that the model captures the intended interpretation, it is necessary to show how it represents the entities of interest in the application domain. For consistency, this section defines model structures called nested graph models (NGMs), which can serve as the denotation of logical expressions that contain nested contexts. Nested graph models are general enough to represent a variety of other model structures, including Tarski-style "flat" models, the possible worlds of Kripke and Montague, and other approaches discussed in this article. The mapping from those model structures to NGMs shows that NGMs are at least as suitable for capturing the intented interpretation. Dunn's semantics allows NGMs to do more:  the option of representing metalevel information in any context enables statements in one context to talk about the laws and facts of nested contexts and about the intentions of agents who may have legislated the laws.

To illustrate the formal definitions, Figure 6 shows an informal example of an NGM. Every box or rectangle in Figure 6 represents an individual entity in the domain of discourse, and every circle represents a property (monadic predicate) or a relation (predicate or relation with two or more arguments) that is true of the individual(s) to which it is linked. The arrows on the arcs are synonyms for the integers used to label the arcs:  for dyadic relations, an arrow pointing toward the circle represents the integer 1, and an arrow pointing away from the circle represents 2; relations with more than two arcs must supplement the arrows with integers. Some boxes contain nested graphs:  they represent individuals that have parts or aspects, which are individual entities represented by the boxes in the nested graphs.

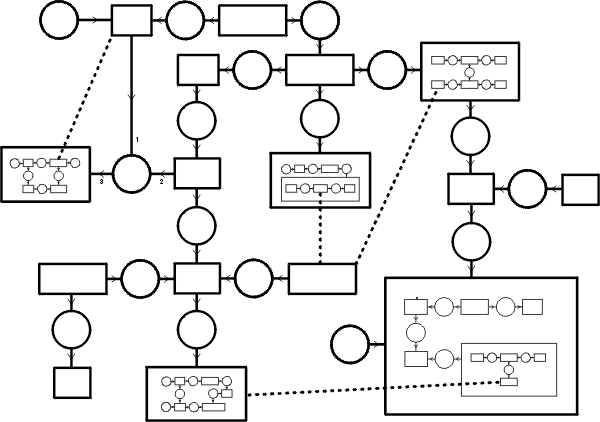
Figure 6:  A nested graph model (NGM)

The four dotted lines in Figure 6 are coreference links, which represent three lines lines of identity. Two lines of identity contain only two boxes, which are the endpoints of a single coreference link. The third line of identity contains three boxes, which are connected by two coreference links. In general, a line of identity with n boxes may be shown by n−1 coreference links, each of which corresponds to an equation that asserts the equality of the referents of the boxes it connects. A coreference link may connect two boxes of the same NGM, or it may connect a box of an NGM G to a box of another NGM that is nested directly or indirectly in G. But a coreference link may never connect a box of an NGM G to a box of another NGM H, where neither G nor H is nested in the other. As Figure 6 illustrates, coreference links may go from an outer NGM to a more deeply nested NGM, but they may not connect boxes in two independently nested NGMs.

For convenience in relating the formalism to diagrams such as Figure 6, the components of a nested graph model (NGM) are called arcs, boxes, circles, labels, and lines of identity. Formally, however, an NGM is defined as a 5-tuple G=(A,B,C,L,I), consisting of five abstract sets whose implications are completely determined by the following definitions:

1. Arcs.  Every arc in A is an ordered pair (c,b), where c is a circle in C and b is a box in B.

2. Boxes.  If b is any box in B, there may be a nested graph model H that is said to be contained in b and directly nested in G. An NGM is said to be nested in G if it is directly nested either in G itself or in some other NGM that is nested in G. The NGM G may not be nested in itself, and any NGM nested in G must be contained in exactly one box of G or of some NGM nested in G. No NGM may be contained in more than one box.

3. Circles.  If c is any circle in C, any arc (c,b) in A is said to belong to c. For any circle c, the number n of arcs that belong to c is finite; and for each i from 1 to n, there is one and only one arc a_i, which belongs to c and for which label(a_i)=i. (If no arcs belong to c, then c represents a proposition constant, which Peirce called a medad.)

4. Labels.  L is a set of entities called labels, for which there exists a function label: A∪B∪C→L. If a is any arc in A, label(a)=i is a positive integer. If b is any box in B, label(b) is said to be an individual identifier; no two boxes in B may have identical labels. If c is any circle in C, label(c) is said to be a relation identifier; any number of circles in C may have identical labels.

5. Lines of Identity.  Every line of identity is a set of two or more boxes. For each i in I, there must exist exactly one NGM H, where either H=G or H is nested in G; one or more boxes of i must be boxes of H, and all other boxes of i must be boxes of some NGM nested in H. (Note:  coreference links, which appear in informal diagrams such as Figures 3 and 6, are not mentioned in the formal definition of lines of identity. Alternative notations, such as variable names, could be used to indicate the boxes that belong to each line of identity.)

6. Outermost context.  The NGM G is said to be the outermost context of G. Any box that contains an NGM H nested in G is said to be a nested context of G.

An NGM may contain any number of levels of nested NGMs, but no NGM may be nested within itself, either directly or indirectly. If an NGM has an infinite nesting depth, it could be isomorphic to another NGM nested in itself; but the nested copy is considered to be distinct from the outer NGM.

Mapping other models to NGMs.  Nested graph models are set-theoretical structures that can serve as models for a wide variety of logical theories. They can be specialized in various ways to represent other model structures. Tarski-style models require no nesting, Kripke-style models require one level of nesting, and models for multiple modalities, which will be discussed in Sections 6 and 7, require deeper nesting.

• Tarski's flat models.  A Tarski-style model M=(D,R,Φ) consists of a nonempty set D called a domain of individuals, a set R of relations defined over D, and an evaluation function Φ. For any first-order proposition p stated in terms of D and R, Φ(p) is a truth value T or F. By the usual methods for representing relations as graphs, the model M can be represented as a flat NGM G=(A,B,C,L,I), for which no box in B contains a nested NGM. Informally, the individuals in D are represented by boxes, and the relations are represented by circles. The labels of the boxes are the names or identifiers of the individuals in D, and the labels of the circles are the names of the relations in R. Formally, the following construction defines an isomorphism from M to G:

  1. Each individual x in the domain D is represented by exactly one box b in B whose label is x:  label(b)=x. For any x in D, the inverse label^-1(x) is the box in B that represents x.

  2. Each tuple t=(x₁,...,x_n) of any n-adic relation r in R is represented by a circle c in C, and label(c)=r. The inverse label^-1(r) is a subset of C, which contains exactly one circle for every tuple of r.

  3. For each i from 1 to n, the i-th arc of the circle c for the tuple t is the pair (c, label^-1(x_i)). That arc is labeled with the integer i, and it is said to link c to the box labeled x_i.

  4. The sets A, B, C, and L contain no elements other than those specified in steps 1, 2, and 3.

  5. There are no lines of identity:  the set I is empty.

  6. Since this construction defines a unique NGM G that is isomorphic to M, the definition of Φ(p) in terms of D and R can be mapped to an equivalent evaluation funcdtion Ψ(p) in terms of G.

  For finite models, these steps can be translated to a computer program that constructs G from M and Ψ from Φ. For infinite models, they should be considered a specification rather than a construction. By this specification, D and R are subsets of L. Therefore, there would always be enough labels for the boxes and circles, even if D and R happen to be uncoutably infinite.

• Kripke's possible worlds.  Any Kripke model structure M=(K,R,Φ) can be represented by a nested graph model with one level of nesting. The outermost context of G contains one box for every world w in K and one circle for every pair (w_i,w_j) in the accessibility relation R. Figure 7 shows such an NGM in which each of the five outer boxes contains a nested NGM that represents a Tarski-style model of some possible world.
  

  Figure 7:  An NGM that represents a Kripke model structure

  The box labeled w₀ represents the real world, and the boxes labeled w₁ to w₄ represent worlds that are accessible from the real world. The circles labeled R represent instances of the accessibility relation, and the arrows show which worlds are accessible from any other. Formally, the following construction defines an isomorphism from any Kripke model structure M to an NGM G=(A,B,C,L,I):

  1. For each possible world w_i in K, let the set B have a box b_i, which contains a flat NGM W that represents a Tarski-style model for w_i. Let the label of the box b_i be the world w_i.

  2. For each pair (w_i,w_j) in the accessibility relation R, let the set C have a circle c with the label "R", and let the set A have two arcs:  an arc (c,b_i) with the label "1" and an arc (c,b_j) with the label "2". (In Figure 7, an arrow pointing toward the circle marks arc 1, and an arrow pointing away marks arc 2.)

  3. The sets A, B, and C have no elements other than those specified in steps 1 and 2. Let the set L be the union of all the labels specified in those steps:  L=K∪{"R","1","2"}. The arcs, boxes, circles, and labels in any NGM W nested in a box b_i in B are derived from the Tarski-style model for the world w_i.

  4. There are no lines of identity:  the set I is empty.

  5. Since this construction defines a unique NGM G that is isomorphic to M, the definition of Φ for M can be mapped to an equivalent evaluation function Ψ for G.

• Models for quantified modal logic.  Kripke's original model theory was designed for propositional modal logic, which does not support quantified variables that range over individuals. When quantification is added to modal logic, variables may refer to individuals that "exist" in more than one world. Figure 8 shows an extension to the Kripke models that allows individuals in one world to have counterparts in other worlds.
  

  Figure 8:  An NGM with counterparts in multiple worlds

  At the top of Figure 8, two individuals, represented by boxes labeled a and b, are connected by coreference links to some of the boxes of the nested graphs. The box labeled w₀ represents a Tarski-style model for the real world, in which two individuals are marked as identical to a and b by coreference links. The box labeled w₁ represents some possible world in which two individuals are marked as counterparts for a and b by coreference links, and w₂ represents another possible world in which only one individual has a counterpart for b. The two coreference links attached to box a represent a line of identity that contains three boxes, and the three coreference links attached to box b represent a line of identity that contains four boxes.

  An NGM for quantified modal logic, G=(A,B,C,L,I), can be constructed by starting with the first three steps for an NGM for a Kripke-style model and continuing with the following:

  1. For every individual x that has counterparts in two or more worlds, add x to the set of labels L.

  2. Add a box b to B with label(b)=x.

  3. For every world w that has a counterpart of x, there must be a nested NGM that has some box b_w that represents x.

  4. Add a line of identity i to I consisting of the box b from step #2 and every b_w from step #3:

     i = {b} ∪ {b_w | w is a world that has a counterpart of x}.

  If all the boxes in the line of identity i have the same label, then that label could be considered a rigid identifier of the individual across multiple worlds. This construction, however, does not require rigid identifiers:  the boxes that represent the same individual in different worlds may have different labels.

• Models for temporal logic.  Prior (1968) showed that the operators and ◊ could be interpreted as the temporal operators sometimes and always. That interpretation creates a modal-like version of temporal logic whose semantics can be formalized with Kripke-style models. For such logics, an NGM such as Figure 8 could be interpreted as a model of a sequence of events, in which each w_i represents a snapshot of one event in the sequence, and the relation R represents the next relation of each snapshot to its successor.

  As an example, Figure 8 might represent an encounter between a mouse a and a cat b. At time t = 0, the snapshot w₀ represents a model of an event in which the cat b catches the mouse a. In w₁, b eats a. In w₂, b is licking his lips, but a no longer exists. The cat b has a counterpart in all three snapshots, but the mouse a exists in just the first 2. The boxes in the snapshots that have no links to boxes outside their snapshot represent entities such as actions or aspects of actions, which exist only for the duration of one snapshot.

  Figure 8 illustrates a version of temporal logic in which the snapshots are linearly ordered. An NGM could also represent branching time, in which the snapshots for the future lie on multiple branches, each of which represents a different option that the cat or the mouse might choose. Branching models are especially useful for game-playing programs that analyze options many steps into the future.

• Barcan models.  With quantified modal logic, the quantifiers may interact with the modal operators in various ways. The Barcan formula imposes the strong constraint that the necessity operator commutes with universal quantifiers over individuals:

  (∀x)P(x) ≡ (∀x)P(x).

  In terms of Kripke-style models or NGMs, the Barcan constraint implies that all worlds accessible from a given world must have exactly the same individuals. To enforce that constraint, a Barcan NGM can be defined as a G=(A,B,C,L,I) for quantified modal logic whose boxes B are partitioned in an equivalence class E with the following properties:

  1. Every e in E is the union of two disjoint sets of boxes, e = B₁ ∪ B₂, where the boxes in B₁ represent individuals and the boxes in B₂ represent worlds.

  2. For every box b in B₁, b contains no nested NGM, and label(b)=x for some individual x.

  3. For every box b in B₂, b contains a nested NGM H that represents some world w, label(b)=w, and there is an isomorphism f that maps the boxes of H to the boxes in B₁.

  4. For every box b in B₁, there exists a line of identity i in I that consists of the box b and the boxes of each nested NGM that are isomorphic to b:

     i = {b} ∪ {d | d is a box of some NGM nested in a box of B₂ for which f(d)=b}.

  5. There are no lines of identity in I other than those determined in step #4.

  In short, each equivalence class contains a set of individual boxes B₁ and a set of world boxes B₂. Each world box contains a nested NGM whose boxes are in a one-to-one correspondence with the individual boxes of B₁. Each individual box has a coreference link to the corresponding box of each NGM nested in a world box of B₂.

This discussion shows how various Kripke-style models can be converted to isomorphic NGMs. That conversion enables different kinds of model structures to be compared within a common framework. The next two sections of this paper show that NGMs combined with Dunn's semantics can represent a wider range of semantic structures and methods of reasoning.

6. Beyond Kripke Semantics

As the examples in Section 5 show, nested graph models can represent the equivalent of Kripke models for a wide range of logics. But Kripke models, which use only a single level of nesting, do not take full advantage of the representational options of NGMs. The possibility of multiple levels of nesting makes NGMs significantly more expressive than Kripke's model structures, but questions arise about what they actually express. In criticizing Kripke's models, Quine (1972) noted that models can be used to prove that certain axioms are consistent, but they don't explain the intended meaning of those axioms:

The notion of possible world did indeed contribute to the semantics of modal logic, and it behooves us to recognize the nature of its contribution: it led to Kripke's precocious and significant theory of models of modal logic. Models afford consistency proofs; also they have heuristic value; but they do not constitute explication. Models, however clear they be in themselves, may leave us at a loss for the primary, intended interpretation.

To illustrate the issues, Figure 9 shows a conceptual graph with two levels of nesting to represent the sentence Tom believes that Mary wants to marry a sailor. The type labels of the contexts indicate how the nested CGs are interpreted:  what Tom believes is a proposition stated by the CG nested in the context of type Proposition; what Mary wants is a situation described by the proposition stated by the CG nested in the context of type Situation. Relations of type (Expr) show that Tom and Mary are the experiencers of states of believing or wanting, and relations of type (Thme) show that the themes of those states are propositions or situations.

Figure 9:  A conceptual graph with two nested contexts

When a CG is in the outermost context or when it is nested in a concept of type Proposition, it states a proposition. When a CG is nested inside a concept of type Situation, the stated proposition describes the situation. When a context is translated to predicate calculus, the result depends on the type label of the context. In the following translation, the first line represents the subgraph outside the nested contexts, the second line represents the subgraph for Tom's belief, and the third line represents the subgraph for Mary's desire:

(∃a:Person)(∃b:Believe)(name(a,'Tom') ∧ expr(a,b) ∧ thme(b,
     (∃c:Person)(∃d:Want)(∃e:Situation)(name(c,'Mary') ∧ expr(d,c) ∧ thme(d,e) ∧ dscr(e,
          (∃f:Marry)(∃g:Sailor)(agnt(f,c) ∧ thme(f,g))))))

As the translation to predicate calculus illustrates, the nested CG contexts map to formulas that are nested as arguments of predicates, such as thme or dscr. Such graphs or formulas can be treated as examples of Tarski's stratified metalevels, in which a proposition expressed in the outer context can make a statement about a proposition in the nested context, which may in turn make a statement about another proposition nested even more deeply. A nested graph model for such propositions would have the same kind of nested structure.

To show how the denotation of the CG in Figure 9 (or its translation to predicate calculus) is evaluated, consider the NGM in Figure 10, which represents some aspect of the world, including some of Tom's beliefs. The outermost context of Figure 10 represents some information known to an outside observer who uttered the original sentence Tom believes that Mary wants to marry a sailor. The context labeled #4 contains some of Tom's beliefs, including his mistaken belief that person #5 is named Jane, even though #5 is coreferent with person #3, who is known to the outside observer as Mary. The evaluation of Figure 9 in terms of Figure 10 is based on the method of outside-in evaluation, which Peirce (1909) called endoporeutic.

Figure 10:  An NGM for which Figure 9 has denotation true

Syntactically, Figure 10 is a well formed CG, but it is limited to a more primitive subset of features than Figure 9. Before the denotation of Figure 9 can be evaluated in terms of Figure 10, each concept node of the CG must be replaced by a subgraph that uses the same features. The concept [Person: Tom], for example, may be considered an abbreviation for a CG that uses only the primitive features:

(Person)—[∃]→(Name)→["Tom"]—(Word).

For nested CGs, projections are used to evaluate the denotations of subgraphs in each context, but more information must be considered:  the nesting structure, the types of contexts, and the relations attached to the contexts. Figures 9 and 10 illustrate an important special case in which there are no negations, the nesting struture is the same, and the corresponding contexts have the same types and attached relations. For that case, the denotation is true if the subgraph of Figure 9 in each context has a projection into the corresponding subgraph of Figure 10. The evaluation starts from the outside and moves inward:

1. The first step begins by matching the outermost context of Figure 9 to the outermost context of Figure 10. When Figure 9 is converted to the same primitives as Figure 10, the projection succeeds because the outermost part of Figure 9 is identical to a subgraph of Figure 10. If the projection had failed, the denotation would be false, and further evaluation of the nested contexts would be irrelevant.

2. The evaluation continues by determining whether the part of Figure 9 nested one level deep has a projection into the corresponding part of Figure 10. In this case, the projection is blocked because Tom falsely believes that Mary has the name Jane. Nevertheless, the node [#5], which represents Jane in Tom's belief, is coreferent with the outer node [#3], which represents the person whose actual name is Mary. The projection can succeed if the subgraph with the name Mary may be imported (copied) from the outer context to the inner context. Since the original sentence was uttered by somebody who knew Mary's name, the speaker used the name Mary in that context, even though Tom believed she was named Jane. Therefore, the correct name may be used to evaluate the denotation. When the subgraph →(Name)→["Mary"]—(Word) is imported into the context and attached to node [#5], the projection succeeds.

3. Finally, the part of Figure 9 nested two levels deep must have a projection into the corresponding part of Figure 10. In this case, the projection is blocked because concept [#11] is not marked as a sailor. Nevertheless, that node is coreferent with concept [#7], which is marked as a sailor. Since the scope of Tom's belief includes both contexts #4 and #8, the subgraph —(Sailor) may be imported from context #4 and attached to concept [#11]. As a result, the modified version Figure 9 can be projected into the modified version of Figure 10, and the denotation is true.

By supporting multiple levels of nesting, NGMs can represent structures that are significantly richer than Kripke models. But the intended meaning of those structures and the methods for evaluating denotations raise seven key questions:

1. How does Peirce's method of endoporeutic relate to Tarski's method for evaluating the denotation of a formula in first-order logic?

2. To what extent does the nesting increase the expressive power of an NGM in comparison to a Tarski-style relational structure or a Kripke-style model structure?

3. Import rules add a feature that is not present in any version of Tarski's or Kripke's evaulation function. What is their model-theoretic justification?

4. How are NGMs related to Dunn's semantics, Tarski's stratified metalevels, and other semantic theories? How is the NGM formalism related to other graph formalisms, such as SNePS (Shapiro 1979; Shapiro & Rappaport 1992)?

5. The nested contexts are governed by concepts such as Believe and Want, which represent two kinds of propositional attitudes. But natural languages have hundreds or thousands of verbs that express some kind of mental attitude about a proposition stated in a subordinate clause. How could the evaluation function take into account all the conditions implied by each of those verbs or the events they represent?

6. The evaluation of Figure 9 depends on the mental attitudes of several agents, such as Tom, Mary, and an outside observer who presumably uttered the original sentence. Is it always necessary to consider multiple agents and the structure of the linguistic discourse? How can the effects of such interactions be analyzed and formalized in the evaluation function?

7. Finally, what is the ontological status of entities that are supposed to "exist" within a context? What is their "intended interpretation" in Quine's sense? If they don't represent things in possible worlds, what do they represent or correspond to in the real world?

Since Peirce developed endoporeutic about thirty years before Tarski, he never related it to Tarski's approach. But he did relate it to the detailed model-theoretic analyses of medieval logicians such as Ockham (1323). Peirce (1885) used model-theoretic arguments to justify the rules of inference for his algebraic notation for predicate calculus. For existential graphs, Peirce (1909) defined endoporeutic as an evaluation method that is logically equivalent to Tarski's. That equivalence was not recognized until Hilpinen (1982) showed that Peirce's endoporeutic could be viewed as a version of game-theoretical semantics by Hintikka (1973). Sowa (1984) used a game-theoretical method to define the model theory for the first-order subset of conceptual graphs. For an introductory textbook on model theory, Barwise and Etchemendy (1993) adopted game-theoretical semantics because it is easier to explain than Tarski's original method. For evaluating NGMs, it is especially convenient because it can accommodate various extensions, such as import conditions and discourse constraints, while the evaluation progresses from one level of nesting to the next (Hintikka & Kulas 1985).

The flexibility of game-theoretical semantics allows it to accommodate the insights and mechanisms of dynamic semantics, which uses discourse information while determining the semantics of NL sentences (Karttunen 1976; Heim 1982; Groenendijk & Stokhof 1991). Veltman (1996) characterized dynamic semantics by the slogan "You know the meaning of a sentence if you know the change it brings about in the information state of anyone who accepts the news conveyed by it." Dynamic semantics is complementary to Hintikka's game-theoretical semantics and Peirce's endoporeutic.

• Peirce developed endoporeutic as a formalization of Ockham's method of evaluating the truth conditions of sentences in Latin, and Hintikka developed game-theoretical semantics as a simpler but more general method for evaluating truth conditions than Tarski's.

• Karttunen and Heim were addressing the problem of incorporating new information into a semantic representation during natural language discourse. They considered truth conditions to be an important, but solvable problem compared to the many unsolved problems of anaphoric references.

• The method of outside-in evaluation that characterizes both endoporeutic and game-theoretical semantics makes the evaluation procedure more amenable to the introduction of new information. As an example, the evaluation of Figure 9 in terms of Figure 10 allows information to be imported as the evaluation proceeds from one context to the next. The discourse constraints of dynamic semantics can also be enforced as each new context is entered.

Although NGMs can accommodate many kinds of relationships that Tarski and Kripke never considered, they remain within the framework of first-order semantics. In principle, any NGM can be translated to a flat NGM, which can be used to evaluate denotations by Tarski's original approach. As an example, Figure 11 shows a flattened version of Figure 10. In order to preserve information about the nesting structure, the method of flattening attaches an extra argument to show the context of each circle and links each box to its containing context by a relation of type IsIn. Coreference links in the NGM are replaced by a three-argument equality relation (EQ), in which the third argument shows the context in which two individuals are considered to be equal.

Figure 11:  A flattened version of Figure 10

The conversion from Figure 10 to Figure 11 is similar to the translation from the CG notation with nested contexts to Shapiro's SNePS notation, in which nested contexts are replaced by propositional nodes to which the relations are attached. Both notations are capable of expressing logically equivalent information. Formally, any NGM G=(A,B,C,L,I) can be converted to a flat NGM F=(FA,FB,FC,FL,FI) by the following construction:

1. For every box b of G or of any NGM nested in G, let FB have a unique box fb, let label(b) be in FL, and let label(fb) = label(b).

2. For every circle c in G or in any NGM nested in G, let FC have a unique circle fc, let label(c) be in FL, and let label(fc) = label(c).

3. For every arc a=(c,b) in G or in any NGM nested in G, let FA have an arc fa=(fc,fb) where fc is the circle that corresponds to c, fb is the box that corresponds to b, and label(fa) = label(a).

4. Add the strings "IsIn" and "EQ" to the labels in FL. (If step #3 had already introduced either of those labels in FL, then append some string to the previous labels that is sufficient to distinguish them from all other labels in FL.)

5. For every box fb in FB whose corresponding box b contains a nested NGM H, the box fb shall not contain any nested NGM. In addition,
   • For every box d of H whose corresponding box is fd in FB, add a circle e in FC with label(e) = "IsIn" and with two additional arcs in FA:  (e,fd) with label 1 and (e,fb) with label 2.
   • For every circle c of H whose corresponding circle is fc in FC, add an arc (fc,fb) to FA. If c has n arcs, let label((fc,fb))=n+1.

6. Let the set FI be empty, and for every line of identity i in I, let H be the NGM whose boxes have a nonempty overlap with i and all other boxes of i are boxes of some NGM nested in H. Select some box b of H which is also in i and whose corresponding box in FB is fb. For every box d in i other than b whose corresponding box in FB is fd, add a circle c to FC for which label(c)="EQ", add an arc (c,fb) with label 1 to FA, add an arc (c,fd) with label 2 to FA, and if the box fd is linked to a box fx by a circle with the label "IsIn", add an arc (c,fx) with label 3 to FA.

The method used to map a nested graph model to a flat model can be generalized to a method for translating a formalism with nested contexts, such as conceptual graphs, to a formalism with propositional nodes but no nesting, such as SNePS. In effect, the nesting is an explicit reprsentation of Tarski's stratified metalevels, in which higher levels are able to state propositions about both the syntax and semantics of propositions stated at any lower level. When two or more levels are flattened to a single level, additional arguments must be added to the relations in order to indicate which level they came from. The process of flattening demonstrates how a purely first-order model theory is supported:  propositions are represented by nodes that represent individual entities of type Proposition. The flattened models correspond to a Tarski-style model, and the flattened languages are first-order logics, whose denotations can be evaluated by a Tarski-style method.

Although nested contexts do not increase the theoretical complexity beyond first-order logic, they simplify the language by eliminating the extra arguments needed to distinguish contexts in a flat model. The contexts also separate the metalevel propositions about a context from the object-level propositions within a context. That separation facilitates the introduction of Dunn's semantics into the langauge:

1. The modal operators and ◊ or the equivalent CG relations Necs and Psbl make metalevel assertions that the nested propositions they govern are provable from the laws or consistent with the laws.

2. The laws themselves, which are asserted in a metalevel outside the context governed by the modal operators, are all stated in FOL, and conventional theorem provers can be used to check the provability or consistency. (For undecidable logics, only some of the checking my be computable, but that is better than Kripke's primitive accessibility relation, which eliminates any possibility of checking.)

3. Formally, the laws, facts, and propositions governed by the modal operators are all stated in FOL, and conventional theorem provers can be used to check their provability or consistency.

4. Computationally, the separation between the metalevel and the object level allows the two kinds of reasoning to be performed independently, as illustrated by the example in Section 4 about Joe's belief in astrology.

5. Any kind of reasoning that is performed with modal operators defined by Kripke semantics can also be performed when the operators are defined in terms of laws and facts. But Dunn's semantics also makes it possible to perform metametalevel reasoning about the propositions considered as laws or facts. In particular, probabilities and heuristics can be used to select laws at the metametalevel, while logical deduction with those laws is used at the lower levels.

The import rules for copying information compensate for the possibly incomplete information in a context. To use the terms of Reiter (1978), a context represents an open world, in contrast to Hintikka's maximally consistent model sets, which represent closed worlds. Computationally, the infinite model sets contain far too much information to be comprehended or manipulated in any useful way. A context is a finite excerpt from a model set in the same sense that a situation is a finite excerpt from a possible world. Figure 12 shows mappings from a Kripke possible world w to a description of w as a Hintikka model set M or a finite excerpt from w as a Barwise and Perry situation s. Then M and s may be mapped to a McCarthy context C.

From a possible world w, the mapping to the right extracts an excerpt as a situation s, which may be described by the propositions in a context C. From the same world w, the downward mapping leads to a description of w as a model set M, from which an equivalent excerpt would produce the same context C. The symbol |= represents semantic entailment:  w entails M, and s entails C. The ultimate justification for the import rules is the preservation of the truth conditions that make Figure 12 a commutative diagram:  the alternate routes through the diagram must lead to logically equivalent results.

The combined mappings in Figure 12 replace the mysterious possible worlds with finite, computable contexts. Hintikka's model sets support operations on well-defined symbols instead of imaginary worlds, but they may still be infinite. Situations are finite, but like worlds they consist of physical or fictitious objects that are not computable. The contexts in the lower right of Figure 12 are the only things that can be represented and manipulated in a digital computer. Any theory of semantics that is stated in terms of possible worlds, model sets, or situations must ultimately be mapped to a theory of contexts in order to be computable.

The discussion so far has addressed the first four of the seven key questions on page xx. The next section addresses the last three questions, which involve the kinds of verbs that express mental attitudes, the ontological status of the entities they represent, the roles of the agents who have those attitudes, and the methods of reasoning about those attitudes.

7. The Intended Interpretation

Models and worlds have been interpreted in many different ways by people who have formulated theories about them. Some have used models as surrogates for worlds, but Lewis, among others, criticized such "ersatz worlds" as inadequate. In a paper that acknowledged conversations with Lewis, Montague (1967) explained why he objected to "the identification of possible worlds with models":

...two possible worlds may differ even though they may be indistinguishable in all respects expressible in a given language (even by open formulas). For instance, if the language refers only to physical predicates, then we may consider two possible worlds, consisting of exactly the same persons and physical objects, all of which have exactly the same physical properties and stand in exactly the same physical relations; then the two corresponding models for our physical language will be identical. But the two possible worlds may still differ, for example, in that in one everyone believes the proposition that snow is white, while in the other someone does not believe it.... This point might seem unimportant, but it looms large in any attempt to treat belief as a relation between persons and propositions.

In that same paper, Montague outlined his method for reducing "four types of entities — experiences, events, tasks, obligations — to [dyadic] predicates." But he used those predicates in statements governed by modal operators such as obligatory:

Obligations can probably best be regarded as the same sort of things as tasks and experiences, that is, as relations-in-intension between persons and moments; for instance, the obligation to give Smith a horse can be identified with the predicte expressed by 'x gives Smith a horse at t'. We should scrutinize, in this context also, the notion of partaking of a predicate. Notice that if R is an obligation, to say that x bears the relation-in-intension R to t is not to say that x has the obligation R at t, but rather that x discharges or fulfills the obligation R at t. But how could we say that x has at t the obligation R? This would amount to the assertion that it is obligatory at t that x bear the relation-in-intension R to some moment equal to or subsequent to t.

1. Jones has an obligation to give Smith a horse.

2. Obligatory(there exists a time t when Jones gives Smith a horse).

1. The noun obligation had to be eliminated because it implied the existence of an unobservable entity of type Obligation.

2. Since Kripke had previously "solved" the problem of defining modal operators, Montague transformed the noun to an adverb that represents a modal operator.

3. Then Kripke's semantics could define the operator Obligatory in terms of possible worlds and the accessibility relation between worlds.

4. To evaluate the denotation of sentences for his model theory, Montague adopted Carnap's idea that the intension of a sentence could be defined as a function from possible worlds to truth values.

5. To construct those functions from simpler functions, Montague (1970) assigned a lambda expression to every grammar rule for his fragment of English. The parse tree for a sentence would then determine a combination of lambda expressions that would define the intension of a sentence in terms of simpler functions for each part of speech.

6. With this construction, Montague restricted the variables of his logic to refer only to physical objects, never to "experiences, events, tasks, obligations."

Peirce had a much simpler and more realistic theory. For him, thoughts, beliefs, and obligations are signs. The types of signs are independent of any mind or brain, but the particular instances — or tokens as he called them — exist in the brains of individual people, not in an undefined accessibility relation between imaginary worlds. Those people can give evidence of their internal signs by using external signs, such as sentences, contracts, and handshakes. In his definition of sign, Peirce (1902) emphasized its independence of any implementation in proteins or silicon:

I define a sign as something, A, which brings something, B, its interpretant, into the same sort of correspondence with something, C, its object, as that in which itself stands to C. In this definition I make no more reference to anything like the human mind than I do when I define a line as the place within which a particle lies during a lapse of time. (p. 235)

In 1906, Peirce introduced colors into his existential graphs to distinguish various kinds of modality and intentionality. Figure 4, for example, used red to represent possibility in the EG for the sentence You can lead a horse to water, but you can't make him drink. To distinguish the actual, modal, and intentional contexts illustrated in Figure 8, three kinds of colors would be needed. Conveniently, the heraldic tinctures, which were used to paint coats of arms in the middle ages, were grouped in three classes:  metal, color, and fur. Peirce adopted them for his three kinds of contexts, each of which corresponded to one of his three categories: Firstness (independent conception), Secondness (relative conception), and Thirdness (mediating conception).

1. Actuality is Firstness, because it is what it is, independent of anything else. Peirce used the metallic tincture argent (white background) for "the actual or true in a general or ordinary sense," and three other metals (or, fer, and plomb) for "the actual or true in some special sense."

2. Modality is Secondness, because it distinguishes the mode of a situation relative to what is actual:  whenever the actual world changes, the possibilities must also change. Peirce used four heraldic colors to distinguish modalities:  azure for logical possibility (dark blue) and subjective possibility (light blue); gules (red) for objective possibility; vert (green) for "what is in the interrogative mood"; and purpure (purple) for "freedom or ability."

3. Intentionality is Thirdness, because it depends on the mediation of some agent who distinguishes the intended situation from what is actual. Peirce used four heraldic furs for intentionality: sable (gray) for "the metaphysically, or rationally, or secondarily necessitated"; ermine (yellow) for "purpose or intention"; vair (brown) for "the commanded"; and potent (orange) for "the compelled."

Throughout his analyses, Peirce distinguished the logical operators, such as ∧, ~, and ∃, from the tinctures, which, he said, do not represent

...differences of the predicates, or significations of the graphs, but of the predetermined objects to which the graphs are intended to refer. Consequently, the Iconic idea of the System requires that they should be represented, not by differentiations of the Graphs themselves but by appropriate visible characters of the surfaces upon which the Graphs are marked.

The nature of the universe or universes of discourse (for several may be referred to in a single assertion) in the rather unusual cases in which such precision is required, is denoted either by using modifications of the heraldic tinctures, marked in something like the usual manner in pale ink upon the surface, or by scribing the graphs in colored inks.

Classifying contexts.  Reasoning about modality requires a classification of the types of contexts, their relationships to one another, and the identification of certain propositions in a context as laws or facts. Any of the tinctured contexts may be nested inside or outside the ovals representing negation. When combined with negation in all possible ways, each tincture can represent a family of related modalities:

1. The first metallic tincture, argent, corresponds to the white background that Peirce used for his original existential graphs. When combined with existence and conjunction, negations on a white background support classical first-order logic about what is actually true or false "in an ordinary sense." Negations on the other metallic backgrounds support FOL for what is "actual in some special sense." A statement about the physical world, for example, would be actual in an ordinary sense. But Peirce also considered mathematical abstractions, such as Cantor's hierarchy of infinite sets, to be actual, but not in the same sense as ordinary physical entities.

2. In the algebraic notation, ◊p means that p is possible. Then necessity p is defined as ~◊~p. Impossibility is represented as ~◊p or equivalently ~p. Instead of the single symbol ◊, Peirce's five colors represent different versions of possibility; for each of them, there is a corresponding interpretation of necessity, impossibility, and contingency:

   • Logical possibility.  A dark blue context, Peirce's equivalent of ◊p, would mean that p is consistent or not provably false. His version of p, represented as dark blue between two negations, would therefore mean that p is provable. Impossible ~◊p would mean inconsistent or provably false.

   • Subjective possibility.  In light blue, ◊p would mean that p is believable or not known to be false. p would mean that p is known or not believably false. This interpretation of ◊ and is called epistemic logic.

   • Objective possibility.  In red, ◊p would mean that p is physically possible. As an example, Peirce noted that it was physically possible for him to raise his arm, even when he was not at the moment doing so. p would mean physical necessity according to the laws of nature.

   • Interrogative mood.  In green, ◊p would mean that p is questioned, and p would mean that p is not questionably false. This interpretation of ◊p corresponds to a proposition p in a Prolog goal or the where-clause of an SQL query.

   • Freedom.  In purple, ◊p would mean that p is free or permissible; p would mean that p is obligatory or not permissibly false; ~◊p would mean that p is not permissible or illegal; and ◊~p would mean that p is permissibly false or optional. This interpretation of ◊ and is called deontic logic.

3. The heraldic furs represent various kinds of intentions, but Peirce did not explore the detailed interactions of the furs with negations or with each other. Don Roberts (1973) suggested some combinations, such as negation with the tinctures gules and potent to represent The quality of mercy is not strained.

Multimodal reasoning.  As the multiple axioms for modal logic indicate, there is no single version that is adequate for all applications. The complexities increase when different interpretations of modality are mixed, as in Peirce's five versions of possibility, which could be represented by colors or by subscripts, such as ◊₁, ◊₂, ..., ◊₅. Each of those modalities is derived from a different set of laws, which interact in various ways with the other laws:

• The combination ₂◊₁p, for example, would mean that it is subjectively necessary that p is logically possible. In other words, someone must know that ◊₁p.

• Since what is known must be true, the following theorem would hold for that combination of modalities:

  ₃◊₁p ⊃ ◊₁p.

By introducing contexts, McCarthy hoped to reduce the proliferation of modalities to a single mechanism of metalevel reasoning about the propositions that are true in a context. By supporting a more detailed representation than the operators ◊ and , the dyadic entailment relation and the triadic legislation relation support metalevel reasoning about the laws, facts, and their implications. Following are some implications of Peirce's five kinds of possibility:

• Logical possibility.  The only statements that are logically necessary are tautologies: those statements that are entailed by the empty set. No special lawgiver is needed for the empty set; alternatively, every agent may be assumed to legislate the empty set:

  {} = {p:Proposition | (∀a:Agent)(∀x:Entity)legislate(a,p,x)}.

  The empty set is the set of all propositions p that every agent a legislates as a law for every entity x.

• Subjective possibility.  A proposition p is subjectively possible for an agent a if a does not know p to be false. The subjective laws for any agent a are all the propositions that a knows:

  SubjectiveLaws(a) = {p:Proposition | know(a,p)}.

  That principle of subjective possibility can be stated in the following axiom:

  (∀a:Agent)(∀p:Proposition)(∀x:Entity) (legislate(a,p,x) ≡ know(a, x|=p)).

  For any agent a, proposition p, and entity x, the agent a legislates p as a law for x if and only if a knows that x entails p.

• Objective possibility.  The laws of nature define what is physically possible. The symbol God may be used as a place holder for the lawgiver:

  LawsOfNature = {p:Proposition | (∀x:Entity)legislate(God,p,x)}.

  If God is assumed to be omniscient, this set is the same as everything God knows or SubjectiveLaws(God). What is subjective for God is objective for everyone else.

• Interrogative mood.  A proposition is not questioned if it is part of the common knowledge of the parties to a conversation. For two agents a and b, common knowledge can be defined as the intersection of their subjective knowledge or laws:

  CommonKnowledge(a,b) = SubjectiveLaws(a) ∩ SubjectiveLaws(b).

• Freedom.  Whatever is free or permissible is consistent with the laws, rules, regulations, ordnances, or policies of some lawgiver who has the authority to legislate what is obligatory for x:

  Obligatory(x) = {p:Proposition | (∃a:Agent)(authority(a,x) ∧ legislate(a,p,x)}.

  This interpretation, which defines deontic logic, makes it a weak version of modal logic since consistency is weaker than truth. The usual modal axioms p⊃p and p⊃◊p do not hold for deontic logic, since people can and do violate laws.

To relate events to the agents who form plans and execute them, Bratman (1987) distinguished three determining factors:  beliefs, desires, and intentions (BDI). He insisted that all three are essential and that none of them can be reduced to the other two. Peirce would have agreed:  the appetitive aspect of desire is a kind of Firstness; belief is a kind of Secondness that relates a proposition to a situation; and intention is a kind of Thirdness that relates an agent, a situation, and the agent's plan for action in the situation. To formalize Bratman's theory in Kripke-style model structures, Cohen and Levesque (1990) extended Kripke's triples to BDI octuples of the form (Θ,P,E,Agnt,T,B,G,Φ):

1. Θ is a set of entities called things;

2. P is a set of entities called people;

3. E is a set of event types;

4. Agnt is a function defined over events, which specifies some entity in P as the agent of the event;

5. T is a set of possible worlds or courses of events, each of which is a function from a sequence Z of time points to event types in E;

6. B(w₁,p,t,w₂) is a belief accessibility relation, which relates a course of events w₁, a person p, and a time point t to some course of events w₂ that is accessible from w₁ according to p's beliefs;

7. G(w₁,p,t,w₂) is a goal accessibility relation, which relates a course of events w₁, a person p, and a time point t to some course of events w₂ that is accessible from w₁ according to p's goals;

8. Φ is an evaluation function similar to Kripke's Φ.

The list of features in the BDI octuples is a good summary of the kinds of information that any formalization of intentionality must accommodate. But it also demonstrates the limitations of Kripke-style models in comparison to the more general nested graph models:

• The multiplicity of Greek letters and subscripts tends to frighten nonmathemticians, but it is not a serious defect of the formalism. NGMs would represent logically equivalent information in a more readable form, but with no reduction in the total amount.

• A more serious limitation is the information that BDI octuples leave as undefined primitives:  the belief accessibility relation B and the goal accessibility relation G. With Dunn's semantics, B and G would be replaced by selections of laws and facts, which explain why some courses of events are accessible from others.

• The sets Θ, P, and E constitute an ontology with only three concept types:  Thing, Person, and Event (which is actually the supertype of an open-ended number of event types). A more realistic ontology would require a much richer collection of concept types, their interrelationships, and their associated axioms. Some such ontology is a prerequisite for constructing models, but the definition of the function Φ for evaluating denotations is independent of any particular ontology.

• The set of event types E would correspond to the set of verb senses in natural languages, which has a cardinality between 10⁴ and 10⁵. The function Agnt, which specifies the agent of an event type, is just one of several thematic roles that must be specified for each event type. In addition to the types and roles, an ontology must also specify the definitions and axioms for each type.

• The definitions and axioms of an ontology are the laws that enable Dunn's semantics to derive accessibility relations such as B and G instead of assuming them as undefined primitives.

• The axioms of the ontology and the discourse constraints of dynamic semantics determine the conditions for importing information from one context to another when denotations are evaluated.

• The formal definition of NGMs in Section 5 is general enough to accommodate any ontology for any domain of discourse, and the evaluation methods of Peirce and Hintikka provide a flexible model theory that can support dynamic semantics.

References

Barwise, Jon, & John Etchemendy (1993) Tarski's World, CSLI Publications, Stanford, CA.

Bratman, Michael E. (1987) Intentions, Plans, and Practical Reason, Harvard University Press, Cambridge, MA.

Cohen, Philip R., & Hector J. Levesque (1990) "Intention is choice with commitment," Artificial Intelligence 42:3, 213-261.

Dunn, J. Michael (1973) "A truth value semantics for modal logic," in H. Leblanc, ed., Truth, Syntax and Modality, North-Holland, Amsterdam, pp. 87-100.

Groenendijk, Jeroen, & Martin Stokhof (1991), "Dynamic Predicate Logic", Linguistics and Philosophy 14:1, pp. 39-100.

Heim, Irene R. (1982) The Semantics of Definite and Indefinite Noun Phrases, PhD Dissertation, University of Massachusetts, Amherst. Published (1988) Garland, New York.

Hilpinen, Risto (1982) "On C. S. Peirce's theory of the proposition: Peirce as a precursor of game-theoretical semantics," The Monist 65, 182-88.

Hintikka, Jaakko (1963) "The modes of modality," Acta Philosophica Fennica, Modal and Many-valued Logics, pp. 65-81.

Hintikka, Jaakko (1973) Logic, Language Games, and Information, Clarendon Press, Oxford.

Hintikka, Jaakko, & Jack Kulas (1985) The Game of Language: Studies in Game-Theoretical Semantics and its Applications, D. Reidel, Dordrecht.

Hughes, G. E., & M. J. Cresswell (1968) An Introduction to Modal Logic, Methuen, London.

Kamp, Hans (1981) "Events, discourse representations, and temporal references," Langages 64, 39-64.

Kamp, Hans, & Uwe Reyle (1993) From Discourse to Logic, Kluwer, Dordrecht.

Karttunen, Lauri (1976) "Discourse referents," in J. McCawley, ed., Syntax and Semantics vol. 7, Academic Press, New York, pp. 363-385.

Kripke, Saul A. (1963) "Semantical analysis of modal logic I," Zeitschrift für mathematische Logik und Grundlagen der Mathematik 9, 67-96.

Kripke, Saul A. (1965) "Semantical analysis of modal logic II: Non-normal modal propositional calculi," in J. W. Addison, Leon Henkin, & Alfred Tarski (1965) The Theory of Models, North-Holland Publishing Co., Amsterdam, pp. 206-220.

Lewis, David K. (1986) On the Plurality of Worlds, Basil Blackwell, Oxford.

McCarthy, John (1977) "Epistemological problems of artificial intelligence," Proceedings of IJCAI-77, reprinted in J. McCarthy, Formalizing Common Sense, Ablex, Norwood, NJ.

McCarthy, John (1993) "Notes on formalizing context," Proc. IJCAI-93, Chambéry, France, pp. 555-560.

Montague, Richard (1967) "On the nature of certain philosophical entities," originally published in The Monist 53 (1960), revised version in Montague (1974) pp. 148-187.

Montague, Richard (1970) "The proper treatment of quantification in ordinary English," reprinted in Montague (1974), pp. 247-270.

Montague, Richard (1974) Formal Philosophy, Yale University Press, New Haven.

Ockham, William of (1323) Summa Logicae, Johannes Higman, Paris, 1488. The edition owned by C. S. Peirce.

Peirce, Charles Sanders (1880) "On the algebra of logic," American Journal of Mathematics 3, 15-57.

Peirce, Charles Sanders (1885) "On the algebra of logic," American Journal of Mathematics 7, 180-202.

Peirce, Charles Sanders (1902) Logic, Considered as Semeiotic, MS L75, edited by Joseph Ransdell, http://members.door.net/arisbe/menu/LIBRARY/bycsp/L75/ver1/l75v1-01.htm

Peirce, Charles Sanders (1906) "Prolegomena to an apology for pragmaticism," The Monist, vol. 16, pp. 492-497.

Peirce, Charles Sanders (1909) Manuscript 514, with commentary by J. F. Sowa, available at http://www.jfsowa.com/peirce/ms514.htm

Prior, Arthur N. (1968) Papers on Time and Tense, revised edition ed. by P. Hasle, P. Øhrstrøm, T. Braüner, & B. J. Copeland, Oxford University Press, 2003.

Quine, Willard Van Orman (1972) "Responding to Saul Kripke," reprinted in Quine, Theories and Things, Harvard University Press,

Roberts, Don D. (1973) The Existential Graphs of Charles S. Peirce, Mouton, The Hague.

Shapiro, Stuart C. (1979) "The SNePS semantic network processing system," in N. V. Findler, ed., Associative Networks: Representation and Use of Knowledge by Computers, Academic Press, New York, pp. 263-315.

Shapiro, Stuart C., & William J. Rapaport (1992) "The SNePS family," in F. Lehmann, ed., Semantic Networks in Artificial Intelligence, Pergamon Press, Oxford.

Sowa, John F. (1984) Conceptual Structures: Information Processing in Mind and Machine, Addison-Wesley, Reading, MA.

Sowa, John F. (1995) "Syntax, semantics, and pragmatics of contexts," in Ellis et al. (1995) Conceptual Structures: Applications, Implementation, and Theory, Lecture Notes in #AI 954, Springer-Verlag, Berlin, pp. 1-15.

Sowa, John F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole Publishing Co., Pacific Grove, CA.

Tarski, Alfred (1933) "Pojecie prawdy w jezykach nauk dedukcynych," German trans. as "Der Wahrheitsbegriff in den formalisierten Sprachen," English trans. as "The concept of truth in formalized languages," in Tarski, Logic, Semantics, Metamathematics, second edition, Hackett Publishing Co., Indianapolis, pp. 152-278.

Thomason, Richmond H. (2001) "Review of Formal Aspects of Context edited by Bonzon et al.," Computational Linguistics 27:4, 598-600.

Veltman, Frank C. (1996), "Defaults in Update Semantics," Journal of Philosophical Logic 25, 221-261.

  Last Modified: