
Figure 1. Tree of Porphyry, as drawn by Peter of Spain (1239)
John F. Sowa
This is an updated version of an article in the Encyclopedia of Artificial Intelligence, Wiley, 1987, second edition, 1992. With some minor changes, all the text from 1992 is included. More recent material and references have been added. For a printable version, see http://www.jfsowa.com/pubs/semnet.pdf
A semantic network or net is a graph structure for representing knowledge in patterns of interconnected nodes and arcs. Computer implementations of semantic networks were first developed for artificial intelligence and machine translation, but earlier versions have long been used in philosophy, psychology, and linguistics. The Giant Global Graph of the Semantic Web is a large semantic network (Berners-Lee et al. 2001; Hendler & van Harmelen 2008).
What is common to all semantic networks is a declarative graphic representation that can be used to represent knowledge and support automated systems for reasoning about the knowledge. Some versions are highly informal, but others are formally defined systems of logic. Following are six of the most common kinds of semantic networks:
Network notations and linear notations are capable of expressing equivalent information. But certain kinds of information are easier to express or process in one form or the other. Since the boundary lines are vague, it is impossible to state necessary and sufficient conditions that include all semantic networks while excluding other systems that are not usually called semantic networks. Section 7 of this article discusses the syntactic mechanisms used to express information in network notations and compares them to the corresponding mechanisms used in linear notations.
The oldest known semantic network was drawn in the 3rd century AD by the Greek philosopher Porphyry in his commentary on Aristotle’s categories. Porphyry used it to illustrate Aristotle’s method of defining categories by specifying the genus or general type and the differentiae that distinguish different subtypes of the same supertype. Figure 1 shows a version of the Tree of Porphyry, as it was drawn by the logician Peter of Spain (1239). It illustrates the categories under Substance, which is called the supreme genus or the most general category.

Figure 1. Tree of Porphyry, as drawn by Peter of Spain (1239)
Despite its age, the Tree of Porphyry represents the common core of all modern hierarchies that are used for defining concept types. In Figure 1, the genus Substance with the differentia material is Body and with the differentia immaterial is Spirit. The modern rule of inheritance is a special case of the Aristotelian syllogisms, which specify the conditions for inheriting properties from supertypes to subtypes: LivingThing inherits material Substance from Body and adds the differentia animate; Human inherits sensitive animate material Substance and adds the differentia rational. Aristotle, Porphyry, and the medieval logicians also distinguished the categories or universals from the individual instances or particulars, which are listed at the bottom of Figure 1. Aristotle’s methods of definition and reasoning are still used in artificial intelligence, object-oriented programming languages, and every dictionary from the earliest days to the present.
The first implementations of semantic networks were used to define concept types and patterns of relations for machine translation (MT). Silvio Ceccato (1961) developed correlational nets, which were based on 56 different relations, including subtype, instance, part-whole, case relations, kinship relations, and various kinds of attributes. He used the correlations as patterns for guiding a parser and resolving syntactic ambiguities. Margaret Masterman and her colleagues at the Cambridge Language Research Unit (CLRU) designed the first systems to be called semantic networks. The first published use of the term was in a proposal by Richard Richens (1956) for the “preprogramming” of an MT system:
I refer now to the construction of an interlingua in which all the structural peculiarities of the base language are removed and we are left with what I shall call a “semantic net” of “naked ideas.”Masterman (1961) developed a list of 100 primitive concept types, such as Folk, Stuff, Thing, Do, and Be. She organized the concept types in a lattice, which permits inheritance from multiple supertypes. The CLRU group used those primitives as the basis for defining a conceptual dictionary of 15,000 entries. The basic principles and even many of the primitive concepts have survived in more recent systems of preference semantics (Wilks & Fass 1992).
Among current systems, the description logics include the features of the Tree of Porphyry as a minimum, but they usually add various extensions. They are derived from an approach proposed by Woods (1975) and implemented by Brachman (1979) in a system called Knowledge Language One (KL-ONE). As an example, Figure 2 shows a KL-ONE network that defines the concepts Truck and TrailerTruck as subtypes of Vehicle.

Figure 2. Truck and TrailerTruck concepts defined in KL-ONE
Figure 2 has nine ovals for concept nodes and nine arrows, which represent different kinds of links. The white ovals represent generic concepts for the types, as distinguished from the shaded oval, which is an individual concept for the instance 18. Integer is a built-in or primitive type. The concepts Truck and TrailerTruck are defined in Figure 2, but Vehicle, Trailer, WtMeasure, and VolMeasure would have to be defined by other KL-ONE diagrams.
The double-line arrows represent subtype-supertype links from TrailerTruck to Truck and from Truck to Vehicle. The arrows with a circle in the middle represent roles. The Truck node has four roles labeled UnloadedWt, MaxGrossWt, CargoCapacity, and NumberOfWheels. The TrailerTruck node has two roles, one labeled HasPart and one that restricts the NumberOfWheels role of Truck to the value 18. The notation v/r at the target end of the role arrows indicates value restrictions or type constraints on the permissible values for those roles.
The information in Figure 2 could be represented in Aristotle’s syllogisms by the following two statements. For readability, the second sentence is indented to make it resemble the notation used for frames. It could be split into multiple sentences and recombined by the logics developed by medieval Scholastics, such as William of Ockham (1323).
Every truck is a vehicle.Every trailer truck is a truck that has
as part a trailer,
an unloaded weight, which is a weight measure,
a maximum gross weight, which is a weight measure,
a cargo capacity, which is a volume measure,
and a number of wheels, which is the integer 18.
The tree of Porphyry, KL-ONE, and most description logics are subsets of classical first-order logic (FOL). They belong to the class of monotonic logics, in which new information monotonically increases the number of provable theorems, and none of the old information can ever be deleted or modified. Some versions of description logic support nonmonotonic reasoning, which allows default rules to add optional information and canceling rules to block inherited information. Such systems can be useful for many applications, but they can also create problems of conflicting defaults, as illustrated in Figure 3.

Figure 3. Conflicting defaults in a definitional network
The Nixon diamond on the left shows a conflict caused by inheritance from two different supertypes: by default, Quakers are pacifists, and Republicans are not pacifists. Does Nixon inherit pacifism along the Quaker path, or is it blocked by the negation on the Republican path? On the right is another diamond in which the subtype RoyalElephant cancels the property of being gray, which is the default color for ordinary elephants. If Clyde is first mentioned as an elephant, his default color would be gray, but later information that he is a RoyalElephant should cause the previous information to be retracted. To resolve such conflicts, many developers have adopted more systematic methods of nonmonotonic logic and belief revision that can guarantee global consistency.
Although the basic methods of description logics are as old as Aristotle, they remain a vital part of many hybrid systems, as described in Section 6 below. Much of the ongoing research on description logics has been devoted to increasing their expressive power while remaining within an efficiently computable subset of logic (Brachman et al. 1991; Woods & Schmolze 1992; Baader et al. 2008). Today, the description logic OWL is widely used for representing knowledge in the Semantic Web. But most applications of OWL use only the EL subset, which can be represented by Aristotle’s syllogisms. The EL++ subset has some features that go beyond Aristotle (Hoekstra 2007).
Gottlob Frege (1879) developed a tree notation for the first complete version of first-order logic — his Begriffsschrift or concept writing. Charles Sanders Peirce (1880, 1885) independently developed an algebraic notation, which with a change of symbols by Peano (1889) has become the modern notation for predicate calculus. Although Peirce invented the algebraic notation, he was never fully satisfied with it. As early as 1882, he was searching for a graphic notation, similar to the notations used in organic chemistry, that would more clearly show “the atoms and molecules of logic.” Figure 4 shows one of his relational graphs, which represents the sentence, A Stagirite teacher of a Macedonian conqueror of the world is a disciple and an opponent of a philosopher admired by Church Fathers.

Figure 4. A relational graph
Figure 4 contains three branching lines of identity, each of which corresponds to an existentially quantified variable in the algebraic notation. The words and phrases attached to those lines correspond to the relations or predicates in the algebraic notation. With that correspondence, Figure 4 can be translated to the following formula in predicate calculus:
(∃x)(∃y)(∃z)(isStagirite(x) ∧ teaches(x,y) ∧ isMacedonian(y) ∧ conquersTheWorld(y) ∧ isDiscipleOf(y,z) ∧ isOpponentOf(y,z) ∧ isAdmiredByChurchFathers(z) ).As this formula illustrates, a relational graph can only represent two logical operators: the conjunction ∧ and the existential quantifier ∃. This is the same subset of logic that is represented in the Semantic Web by RDF (Resource Description Framework). The blank nodes in RDF correspond to existential quantifiers.
Other operators, such as negation ~, disjunction ∨, implication ⊃, and the universal quantifier ∀, are more difficult to express because they require some method for demarcating the scope — that part of the formula that is governed by the operator. The problem of representing scope, which Peirce faced in his graphs of 1882, also plagued the early semantic networks used in artificial intelligence 80 years later.
In 1897, Peirce made a simple, but brilliant discovery that solved all the problems at once: he introduced an oval that could enclose and negate an arbitrarily large graph or subgraph. Then combinations of ovals with conjunction and the existential quantifier could express all the logical operators used in the algebraic notation (Peirce 1909). That innovation transformed the relational graphs into the system of existential graphs (EG), which Peirce called “the logic of the future” (Roberts 1973). The implication ⊃, for example, could be represented with a nest of two ovals, since (p⊃q) is equivalent to ~(p∧~q). At the left of Figure 5 is an existential graph for the sentence If a farmer owns a donkey, then he beats it.

Figure 5. EG and DRS for If a farmer owns a donkey, then he beats it.
The outer oval of Figure 5 is the antecedent or if part, which contains farmer, linked by a line representing (∃x) to owns, which is linked by a line representing (∃y) to donkey. The subgraph in the outer oval may be read If a farmer x owns a donkey y. The lines x and y are extended into the inner oval, which represents the consequent, then x beats y. Figure 5 may be translated to the following algebraic formula:
~(∃x)(∃y)(farmer(x) ∧ donkey(y) ∧ owns(x,y) ∧ ~beats(x,y)).This formula is equivalent to
(∀x)(∀y)((farmer(x) ∧ donkey(y) ∧ owns(x,y)) ⊃ beats(x,y)).For comparison, the diagram on the right of Figure 5 is a discourse representation structure (DRS), which Hans Kamp (1981) invented to represent natural language semantics. As their default operators, Peirce and Kamp adopted the existential quantifier (∃) and conjunction (∧). Instead of nested ovals, Kamp used boxes linked by arrows; instead of lines of identity, he used variables. But the logical structures are formally equivalent: they both map to the same formulas in predicate calculus, and the same techniques for analyzing and representing NL semantics can be used with either notation.
As an example that uses disjunction, Figure 6 shows an EG (top) and a DRS (bottom) for the sentence Either Jones owns a book on semantics, Smith owns a book on logic, or Cooper owns a book on unicorns. Below the EG is the corresponding DRS, as drawn by Kamp and Reyle (1993:210).

Figure 6. EG and DRS for representing a disjunction
Since the names Jones, Smith, and Cooper may be true of many individuals, both the EG and the DRS represent them by predicates rather than constants. In both diagrams, the existential quantifiers for Jones, Smith, and Cooper are in the outer area, but the quantifiers for the three books are inside the alternatives. Both diagrams can be mapped to exactly the same formula:
(∃x)(∃y)(∃z)(Jones(x) ∧ Smith(y)) ∧ Cooper(z) ∧
( (∃u)(owns(x,u) ∧ book_on_semantics(u)) ∨
(∃v)(owns(x,v) ∧ book_on_logic(v)) ∨
(∃w)(owns(x,w) ∧ book_on_unicorns(w)) ) )
In linguistics, Lucien Tesnière (1959) developed graph notations for his system of dependency grammar. Figure 7 shows one of his graphs for an epigram by Voltaire, L’autre jour, au fond d’un vallon, un serpent piqua Jean Fréron (The other day, at the bottom of a valley, a snake stung Jean Fréron). At the top is the verb piqua (stung), from which the words that depend directly on the verb are hanging: the subject (serpent), the object (Jean), and two prepositional phrases. The bull’s eye symbol indicates an implicit preposition (à). Every word other than piqua is hanging below some word on which it depends.

Figure 7. A dependency graph in Tesnière’s notation
Tesnière has had a major influence on linguistic theories that place more emphasis on semantics than on syntax. David Hays (1964) presented dependency theory as a formal alternative to Chomsky’s syntactic notations. Klein and Simmons (1963) adopted it for a machine translation system. Valency theory (Allerton 1982) and Meaning-Text Theory (Mel'čuk 1973; Steele 1990) are two ongoing developments of the dependency approach. The dependency theories have also been strongly influenced by case grammar (Fillmore 1968), which provides a convenient set of labels for the arcs of the graphs (Somers 1987).
Under the influence of Hays and Simmons, Roger Schank adopted the dependency approach, but shifted the emphasis to concepts rather than words (Schank & Tesler 1969; Schank 1975). Figure 8 shows a conceptual dependency graph for the sentence A dog is greedily eating a bone. Instead of Tesnière’s tree notation, Schank used different kinds of arrows for different relations, such as ⇔ for the agent-verb relation or an arrow marked with o for object. He replaced the verb eat with one of his primitive acts ingest; he replaced adverbs like greedily with adjective forms like greedy; and he added the linked arrows marked with d for direction to show that the bone goes from some unspecified place into the dog (the subscript 1 indicates that the bone went into the same dog that ingested it).

Figure 8. Schank’s notation for conceptual dependencies
Conceptual dependencies were primarily suited to representing information at the sentence level, but Schank and his colleagues later developed notations for representing larger structures, in which the sentence-level dependencies occurred as nested substructures. The larger structures were called scripts (Schank & Abelson 1977), memory organization packets (MOPs), and thematic organization packets (TOPs) (Schank 1982). To learn or discover the larger structures automatically, case-based reasoning has been used to search for commonly occurring patterns among the lower-level conceptual dependencies (Schank et al. 1994).
Logically, Tesnière’s dependency graphs have the same expressive power as Peirce’s relational graphs of 1882: the only logical operators they can represent are conjunction and the existential quantifier. Even when those graphs have nodes marked with other logical operators, such as disjunction, negation, or the universal quantifier, they fail to express their scope correctly. During the 1970s, various network notations were developed to represent the scope of logical operators. The most successful approach was the method of adding explicit nodes to show propositions. Logical operators would connect the propositional nodes, and relations would either be attached to the propositional nodes or be nested inside them. By those criteria, Frege’s Begriffsschrift, Peirce’s existential graphs, and Kamp’s discourse representation structures could be called propositional semantic networks. In Figure 5, for example, the two EG ovals and the two DRS boxes represent propositions, each of which contains nested propositions.
The first propositional semantic network to be implemented in AI was the MIND system, developed by Stuart Shapiro (1971). It later evolved into the Semantic Network Processing System (SNePS), which has been used to represent a wide range of features in natural language semantics (Shapiro 1979; Maida & Shapiro 1982; Shapiro & Rappaport 1992). Figure 9 shows the SNePS representation for the sentence Sue thinks that Bob believes that a dog is eating a bone. Each of the nodes labeled M1 through M5 represents a distinct proposition, whose relational content is attached to the propositional node.

Figure 9. Propositions represented in SNePS
The proposition M1 states that Sue is the experiencer (Expr) of the verb think, whose theme (Thme) is another proposition M2. For M2, the experiencer is Bob, the verb is believe, and the theme is a proposition M3. For M3, the agent (Agnt) is some entity B1, which is a member of the class Dog, the verb is eat, and the patient (Ptnt) is an entity B2, which is a member of the class Bone. As Figure 9 illustrates, propositions may be used at the metalevel to make statements about other propositions: M1 states that M2 is thought by Sue, and M2 states that M3 is believed by Bob.
Conceptual graphs (Sowa 1976, 2008) are a variety of propositional semantic networks in which the relations are nested inside the propositional nodes. They evolved as a combination of the linguistic features of Tesnière’s dependency graphs and the logical features of Peirce’s existential graphs with strong influences from the work in artificial intelligence and computational linguistics. Figure 10 shows a comparison of Peirce’s EG from Figure 5 with a conceptual graph (CG) that represents the sentence If a farmer owns a donkey, then he beats it.

Figure 10. Comparison of the EG from Figure 5 with a CG for the same sentence
The most obvious differences between the EG and the CG are cosmetic: the ovals are squared off to form boxes, and the implicit negations in the EG are explicitly marked If and Then for better readability. The more subtle differences are in the range of quantification and the point where the quantification occurs. In an EG, a line of identity represents an existential quantifier (∃x) or (∃y), which ranges over anything in the domain of discourse; but in a CG, each box, called a concept, represents a quantifier (∃x:Farmer) or (∃y:Donkey), which is restricted to the type or sort Farmer or Donkey. In the CG, the arcs with arrows indicate the argument of the relations (numbers are used to distinguish the arcs for relations with more than two arguments). As another example, Figure 11 shows the CG that corresponds to the SNePS diagram in Figure 9.

Figure 11. A conceptual graph that corresponds to Figure 9
Figures 8 and 10 both represent the sentence Sue thinks that Bob believes that a dog is eating a bone. The SNePS proposition M1 corresponds to the entire CG in Figure 11; M2 corresponds to the concept box that contains the CG for the nested proposition Bob believes that a dog is eating a bone; and M3 corresponds to the concept box that contains the CG for the more deeply nested proposition A dog is eating a bone. Each concept box in a CG could be considered a separate proposition node that could be translated to a complete sentence by itself. The concept [Dog] could be expressed by the sentence There exists a dog, which corresponds to the SNePS proposition M4. The concept [Person: Sue] expresses the sentence There exists a person named Sue. By such methods, it is possible to translate propositions expressed in SNePS or CGs to equivalent propositions in the other notation. For most sentences, the translations are nearly one-to-one, but sentences that take advantage of special features in one notation may require a more roundabout paraphrase when translated to the other.
Different versions of propositional semantic networks have different syntactic mechanisms for associating the relational content with the propositional nodes, but formal translation rules can be defined for mapping one version to another. Peirce, Sowa, and Kamp used strictly nested propositional enclosures with variables or lines to show coreferences between different enclosures. Frege and Shapiro attached the relations to the propositional nodes (or lines in Frege’s notation). Gary Hendrix (1975, 1979) developed a third option: partitions that enclose the relational content, but with the option of overlapping enclosures if they have common components. Formally, Hendrix’s solution is equivalent to Shapiro’s; but as a practical matter, it is not possible to draw the partitions on a plane sheet if multiple enclosures overlap in complex ways.
An implicational network is a special case of a propositional semantic network in which the primary relation is implication. Other relations may be nested inside the propositional nodes, but they are ignored by the inference procedures. Depending on the interpretation, such networks may be called belief networks, causal networks, Bayesian networks, or truth-maintenance systems. Sometimes the same graph can be used with any or all of these interpretations. Figure 12 shows possible causes for slippery grass: each box represents a proposition, and the arrows show the implications from one proposition to another. If it is the rainy season, the arrow marked T implies that it recently rained; if not, the arrow marked F implies that the sprinkler is in use. For boxes with only one outgoing arrow, the truth of the first proposition implies the truth of the second, but falsity of the first makes no prediction about the second.

Figure 12. An implicational network for reasoning about wet grass
Suppose someone walking across a lawn slips on the grass. Figure 12 represents the kind of background knowledge that the victim might use to reason about the cause. A likely cause of slippery grass is that the grass is wet. It could be wet because either the sprinkler had been in use or it had recently rained. If it is the rainy season, the sprinkler would not be in use. Therefore, it must have rained.
The kind of reasoning described in the previous paragraph can be performed by various AI systems. Chuck Rieger (1976) developed a version of causal networks, which he used for analyzing problem descriptions in English and translating them to a network that could support metalevel reasoning. Benjamin Kuipers (1984, 1994), who was strongly influenced by Rieger’s approach, developed methods of qualitative reasoning, which serve as a bridge between the symbolic methods of AI and the differential equations used in physics and engineering. Judea Pearl (1988, 2000), who has developed techniques for applying statistics and probability to AI, introduced belief networks, which are causal networks whose links are labeled with probabilities.
Different methods of reasoning can be applied to the same basic graph, such as Figure 12. Nodes of the graph may be annotated with truth values, probabilities, or fuzzy values. The choice of two truth values {T,F} or a continuous range of values distinguishes the two major approaches:
Although implicational networks emphasize implication, they are capable of expressing all the Boolean connectives by allowing a conjunction of inputs to a propositional node and a disjunction of outputs. Gerhard Gentzen (1935) showed that a collection of implications in that form could express all of propositional logic. Following is the general form of an implication written in Gentzen’s clause form:
p1, ..., pn ⇒ q1, ..., qmThe p’s are called the antecedents of the implication, and the q’s are called the consequents. The generalized rule of modus ponens states that when every one of the antecedents is true, at least one of the consequents must be true. In effect, the commas in the antecedent have the effect of and operators, and the commas in the consequent have the effect of or operators. Doyle’s original TMS only allowed one term in the consequent. That option, called Horn-clause logic, is widely used for rule-based systems. To support full propositional logic, later versions of TMS allow multiple or operators in the consequent.
Executable semantic networks contain mechanisms that can cause some change to the network itself. The executable mechanisms distinguish them from networks that are static data structures, which can only change through the action of programs external to the net itself. Three kinds of mechanisms are commonly used with executable semantic networks:
An important class of executable networks was inspired by the work of the psychologist Otto Selz (1913, 1922), who was dissatisfied with the undirected associationist theories that were then current. As an alternative, Selz proposed schematic anticipation as a goal-directed method of focusing the thought processes on the task of filling empty slots in a pattern or schema. Figure 13 is an example of a schema that Selz asked his test subjects to complete while he recorded their verbal protocols.

Figure 13. A schema used in Otto Selz’s experiments
The expected answers for the empty slots in Figure 13 are the supertypes of the words at the bottom: the supertype of Newspaper and Magazine is Periodical, and the supertype of Periodical and Book is Publication. This task is actually more difficult in German than in English: Selz’s subjects tried to find a one-word supertype for Zeitung (Newspaper) and Zeitschrift (Magazine), but the correct answer in German is the two-word phrase periodische Druckschrift.
The similarity between Selz’s method of schematic anticipation and the goal-directed methods of AI is not an accident. Two of the pioneers in AI, Herbert Simon and Allen Newell, learned of Selz’s theories from one of their visitors, the psychologist and chessplayer Adriaan de Groot (Simon 1981). In his analysis of chess playing, de Groot (1965) applied Selz’s theories and methods of protocol analysis to the verbal reports of chessplayers ranging from novices to grandmasters. Newell and Simon (1972) adopted Selz’s method of protocol analysis for their study of human problem solving. Their student, Ross Quillian (1966), combined Selz’s networks with the semantic networks used in machine translation. Quillian’s most significant innovation was the marker passing algorithm for spreading activations, which was adopted for later systems, such as NETL by Scott Fahlman (1979) and the massively parallel algorithms by Hendler (1987; 1992) and Shastri (1991; 1992).
The simplest networks with attached procedures are dataflow graphs, which contain passive nodes that hold data and active nodes that take data from input nodes and send results to output nodes. Figure 14 shows a dataflow graph with boxes for the passive nodes and diamonds for the active nodes. The labels on the boxes indicate the data type (Number or String), and the labels on the diamonds indicate the name of the function (+, ×, or convert string to number).
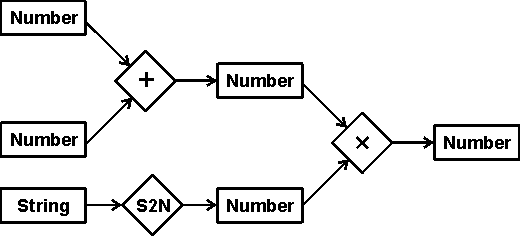
Figure 14. A dataflow graph
For numeric computations, dataflow graphs have little advantage over the algebraic notation used in common programming languages. Figure 14, for example, would correspond to an assignment statement of the following form:
X = (A + B) * S2N(C)Graphic notations are more often used in an Integrated Development Environment (IDE) for linking multiple programs to form a complete system. When dataflow graphs are supplemented with a graphic method for specifying conditions, such as if-then-else, and a way of defining recursive functions, they can form a complete programming language, similar to functional programming languages such as Scheme and ML.
Petri nets, first introduced by Carl Adam Petri (1962), are the most widely-used formalism that combines marker passing with procedures. Like dataflow diagrams, Petri nets have passive nodes, called places, and active nodes, called transitions. In addition, they have a set of rules for marking places with dots, called tokens, and for executing or firing the transitions. To illustrate the flow of tokens, Figure 15 shows a Petri net for a bus stop where three tokens represent people waiting and one token represents an arriving bus.

Figure 15. Petri net for a bus stop
At the upper left of Figure 15, each of the three tokens represents one person waiting at the bus stop. The token at the upper right represents an arriving bus. The transition labeled Bus stops represents an event that fires by removing the token from the arriving place and putting a token in the waiting place. When the bus is waiting, the transition labeled One person gets on bus is enabled because it has at least one token in both of its input places. It fires by first removing one token from both of its input places and putting one token in both of its output places (including the Bus waiting place from which one token had just been removed). As long as the bus is waiting and there are more people waiting, that transition can keep firing. It stops firing when either there are no more people waiting or the Bus starts transition fires by removing the token for the waiting bus and putting a token in the place for Bus leaving.
Each place in a Petri net represents a precondition for the transitions that use it as an input and a postcondition for the transitions that uses it as an output. A token in a place asserts that the corresponding condition is true. By removing a token from each input place, the firing of a transition retracts the assertions of its preconditions. By adding a token to each output place, the firing asserts that each of the postconditions has become true. Petri nets can be used to model or simulate physical events, as in the example of Figure 15. They can also be used to model processes that take place in computer hardware and software; they are especially useful for designing and modeling distributed parallel processes. In Figure 15, each token represents a single bit of information, but an extension, called colored Petri nets, can associate an arbitrary amount of data with each token (Jensen 1992). With such extensions, Petri nets can represent arbitrarily many dataflow graphs running in parallel or simulate the various marker passing algorithms used in semantic networks in the Quillian tradition.
Although dataflow graphs and Petri nets are not usually called semantic networks, similar techniques have been implemented in procedural semantic networks. At the University of Toronto, John Mylopoulos and his students and colleagues have implemented a series of semantic networks with attached procedures (Levesque & Mylopoulos 1979; Mylopoulos 1992). Their systems incorporate definitional networks for defining classes, assertional networks for stating facts, and procedures similar to the methods of object-oriented programming languages. For conceptual graphs, Sowa (1976, 1984) allowed some relation nodes to be replaced by actors, which are functions that form the equivalent of a dataflow graph.
Besides markers and procedures, the third method for making networks executable is to let them grow and change dynamically. Peirce and Selz could also be considered pioneers of that approach. Peirce said that the inference operations on existential graphs could be considered “a moving picture of thought.” For schematic anticipation, Selz considered a schema to be the cause of the neural activity that generates a solution to a problem. Formally, transformations on networks can be defined without reference to the mechanisms that perform the transformations. In Petri nets, for example, the definition states that a transition may “fire” when each of its input nodes contains a token; the mechanism that performs the firing could be internal or external to the transition. For a computer implementation, it may be convenient to treat the networks as passive data structures and to write a program that manipulates them. For a cognitive theory, however, the transformations could be interpreted as network operations initiated and carried out by the network itself. Either interpretation could be consistent with the same formal definitions.
A learning system, natural or artificial, responds to new information by modifying its internal representations in a way that enables the system to respond more effectively to its environment. Systems that use network representations can modify the networks in three ways:
Commercially, rote memory is of enormous importance, since the world economy depends on exact record keeping. For such applications, information is sometimes stored in tables, as in relational databases. But the Semantic Web and related methods are more flexible for information that is not as rigidly structured as a table. However, any information represented in one can be converted to the other. For better efficiency and usability, most database systems add indexes to speed up the search, and they support query languages, such as SQL, which perform transformations to extract and combine the information necessary to answer a request. Since a learning system must be able to distinguish common features and exceptions among similar examples, another feature is essential: the ability to measure similarity and to search the database for networks that are similar, but not identical to any given example.
Neural nets are a widely-used technique for learning by changing the weights assigned to the nodes or arcs of a network. In his study of learning, Thorndike (1932) developed a stimulus-response theory, which he called connectionism: rewards strengthen the S-R connections, and punishments weaken them. Meanwhile, McCulloch and Pitts (1943), a neurophysiologist collaborating with a logician, designed a theoretical model of neural nets that are capable of learning and computing any Boolean function of their inputs. To implement that model, Rosenblatt (1958) built a machine called a perceptron, which simulated the nodes and links of a neural net. Later versions combined connectionism with neural nets, which were simulated on digital computers instead of being implemented directly in hardware. Figure 16 shows a typical neural net with stimuli entering the layer of nodes at the left; the links propagate signals to nodes in one or more hidden layers in the middle; finally, the responses appear at the layer of nodes on the right. The nodes represent neurons, and the links represent dendrites that pass signals from one neuron to another. In computer simulations, each link has an associated weight, which increases or decreases the strength of any signal that passes through the link. Each node combines the strength of all its inputs to determine the value of its output.

Figure 16. A neural net
In a typical neural network, the structure of nodes and arcs is fixed, and the only changes that may occur are the assignments of weights to the arcs. When a new input is presented, the weights on the arcs are combined with the weights on the input features to determine the weights in the hidden layers of the net and ultimately the weights on the outputs. In the learning stage, the system is told whether the predicted weights are correct, and various methods of back propagation are used to adjust the weights on the arcs that lead to the result.
Rote memory is best suited to applications that require exact retrieval of the original data, and methods of changing weights are best suited to pattern recognition. For more versatile and creative kinds of learning, some way of restructuring the network is necessary. But the number of options for reorganizing a network is so vast that the full range of possibilities is largely unexplored. Following are some examples:
For the learning phase, Levinson used a combination of rote learning as in case-based reasoning, restructuring to derive significant generalizations, a similarity measure based on the generalizations, and a method of back propagation to estimate the value of any case that occurred in a game. For playing chess, the cases were board positions represented as graphs. Every position that occurred in a game was stored in a generalization hierarchy, such as those used in definitional networks. At the end of each game, the system used back propagation to adjust the estimated values of each position that led to the win, loss, or draw. When playing a game, the system would examine all legal moves from a given position, search for similar positions in the hierarchy, and choose the move that led to a position whose closest match had the best predicted value.
Complex systems are usually hybrids. A typical example is a combination of HTML for the user interface, a database system for storing data, and a programming language for detailed computation. Most applications of the Semantic Web are hybrids that combine several methods. An example is BabelNet (Navigli & Ponzetto, 2012), which combines techniques for semantic networks, machine translation, and the Semantic Web to learn from and reason with information in the multiple languages of Wikipedia.
For knowledge representation, the Krypton system (Brachman et al. 1983) was a hybrid of KL-ONE for defining a hierarchy of terms (T-Box) with a theorem prover for processing FOL assertions (A-Box). By the same criteria, an order-sorted logic (Cohn 1992) could be called a hybrid: the T-Box is a sort structure that specifies a hierarchy of sorts or types, and the A-box is a version of first-order logic. Most object-oriented programming languages could also be considered hybrids: the C++ language, for example, is a hybrid of a definitional language for specifying a hierarchy of types or classes with the procedural language C for computation.
The most widely used hybrid of multiple network notations is the Unified Modeling Language (UML), which was by designed by three authors, Grady Booch, Ivar Jacobson, and Jim Rumbaugh, who merged their competing notations (Rational Software 1997). Although UML is not usually called a semantic network, its notations can be classified according to the categories of semantic networks discussed in this article:
self.parameter->forAll(p1, p2 | p1.name=p2.name implies p1=p2).In OCL, self refers to the current entity being defined, and the names of functions are written after the entity to which they apply. In predicate calculus, the order would be interchanged: p1.name would be written name(p1). Following is a translation of the OCL statement to predicate calculus with the symbol #self representing the current entity.
(∀p1)(∀p2)
((p1∈parameter(#self) ∧ p2∈parameter(#self) ∧ name(p1)=name(p2))
⊃ p1=p2).
This formula says that for every p1 and
p2, if p1 is a parameter of self
and p2 is a parameter of self and the name
of p1 is equal to the name of p2,
then p1 is equal to p2.
UML has been criticized for a lack of a formal definition, which has resulted in inconsistencies between various implementations (Kent et al. 1999). In response to that criticism, the Object Management Group (2013) developed a formal specification called FUML, which specifies the UML diagrams by a translation to Common Logic (ISO/IEC 2007). The Conceptual Graph Interchange Format (CGIF) is also specified by a translation to Common Logic (Sowa 2008).
Graph notations and linear notations can express logically equivalent information, but with different syntactic conventions. The relational graph in Figure 4 and its translation to a formula in predicate calculus illustrate the differences between the two kinds of notations:
As another example, Petri nets, which are usually expressed in a graphic notation, are formally equivalent to a notation called linear logic. Although Petri nets and linear logic were independently developed by different researchers for different purposes, a commonly used version of Petri nets happens to be isomorphic to a commonly used version of linear logic (Troelstra 1992). Following is a translation of the Petri net of Figure 15 to that version of linear logic:
BusStops: BusArriving ⇒ BusWaiting OnePersonGetsOnBus: PersonWaiting & BusWaiting ⇒ PersonOnBus & BusWaiting BusStarts: BusWaiting ⇒ BusLeaving InitialAssertions: PersonWaiting. PersonWaiting. PersonWaiting. BusArriving.Each arrow (⇒) in this example represents one of the transitions in the Petri net. The feature of linear logic that distinguishes it from classical first-order logic is its treatment of implication. For comparison, following is an application of modus ponens in classical FOL, its replacement in linear logic, and the rule for firing a transition in Petri nets:
One of the major arguments for graphic notations is human readability, but proponents of linear notations often argue that their notations are also highly readable. Each rule in linear logic, for example, is quite readable, but the relationships between rules are not as immediately readable as the direct connections in the Petri net.
As an example, consider the proposition BusWaiting, which is represented by a single place in the Petri net with two inputs and two outputs. That fact can be seen immediately from Figure 15, but a reader would have to search through all of the rules in the linear logic example to verify that the name BusWaiting occurs four times. As examples become larger, any notation become more difficult to read, but the graphic notations still have an advantage over linear notations. Petri nets have been implemented with many thousands of nodes, but it is always possible to look at any node and see immediately how many inputs and outputs it has and where they are linked.
For a system that relates linear and graphic notations, Suzuki et al. (2014) used methods based on Petri nets and dataflow graphs to analyze and transform a linear notation (Prolog) to a Knowledge Transitive Network (KTN). The KTN has both procedural and declarative aspects. As an executable network, a KTN can derive the same results as the original Prolog programs. But as a declarative network, a KTN can be used for deduction, learning, and generating explanations in a natural language.
Besides readability, graphic notations often have heuristic value in helping human readers (either students or researchers) to discover patterns that would be difficult or impossible to see in the linear form. The reason why Peirce called his existential graphs “the logic of the future” was not so much their readability as the direct insight they provided into the structure of proofs. With EGs, Peirce invented the simplest and most elegant rules of inference ever developed for any version of logic. Peirce’s rules, which he discovered in 1897, are a simplification and generalization of the rules of natural deduction that Gentzen (1935) reinvented many years later.
Even today, Peirce’s rules provide insights that have eluded logicians for many years. As an example, Larry Wos (1988) listed 33 unsolved research problems in automated reasoning. Problem 24 asks about the relationship between proofs that use Gentzen’s rules for clauses or his rules of natural deduction:
Is there a mapping between clause representation and natural-deduction representation (and corresponding inference rules and strategies) that causes reasoning programs based respectively on the two approaches or paradigms to attack a given assignment in an essentially identical fashion?The answer follows from theorems that are easy to prove when stated in existential graphs (Sowa 2011, Section 6):
The following six volumes show the evolution of semantic networks and related systems during the past half century. The first three present the historical systems. The last three include systems that continue to be developed and applied in the 21st century.
The following references are cited in the text. Some of them were published in one of the above volumes. Several authors were participants in the 1961 conference.
Allerton, D. J. (1982) Valency and the English Verb, New York: Academic Press.
Baader, Franz, Ian Horrocks, & Ulrike Sattler (2008) Description logics, in van Harmelen, et al. (2008) pp. 135-179.
Bachman, Charles W. (1969) Data structure diagrams, Data Base 1:2, New York: ACM SIGBDP, pp. 4-10.
Basili, Roberto, Maria Teresa Pazienza, & Paola Velardi (1993) Acquisition of selectional patterns from sublanguages, Machine Translation 8.
Basili, Roberto, Maria Teresa Pazienza, & Paola Velardi (1996) An empirical symbolic approach to natural language processing, Artificial Intelligence 85, 59-99.
Berners-Lee, Tim, James Hendler, & Ora Lassila (2001) The Semantic Web, Scientific American, May 2001.
Brachman, Ronald J. (1979) On the epistemological status of semantic networks, in Findler (1979) 3-50.
Brachman, Ronald J., Richard E. Fikes, & Hector J. Levesque (1983) Krypton: A functional approach to knowledge representation, IEEE Computer 16:10, pp. 67-73.
Brachman, Ronald J., Deborah L. McGuinness, Peter F. Patel-Schneider, Lori A. Resnick, & Alex Borgida (1991) Living with Classic: when and how to use a KL-ONE-like language, in Sowa (1991) pp. 401-456.
Brewka, Gerhard, Ilkka Niemelä, & Mirosław Truszczyński (2008) in van Harmelen et al. (2008) pp. 239-284.
Ceccato, Silvio (1961) Linguistic Analysis and Programming for Mechanical Translation, Gordon and Breach, New York.
Chen, Peter Pin-Shan (1976) The entity-relationship model—toward a unified view of data, ACM Transactions on Database Systems 1:1, pp. 9-36.
Cohn, Anthony G. (1992) Completing sort hierarchies, in Lehmann (1992), pp. 477-491.
Dau, Frithjof (2006). Some notes on proofs with Alpha graphs. In Conceptual Structures: Inspiration and Application, (LNAI 4068), H. Schärfe, P. Hitzler, and P. Øhrstrom (eds.), Berlin: Springer. pp. 172-188.
de Groot, Adriaan D. (1965) Thought and Choice in Chess, The Hague: Mouton.
Fahlman, Scott E. (1979) NETL: A System for Representing and Using Real-World Knowledge, Cambridge, MA: MIT Press.
Fillmore, Charles J. (1968) The case for case in E. Bach & R. T. Harms, eds., Universals in Linguistic Theory, New York: Holt, Rinehart and Winston, pp. 1-88.
Frege, Gottlob (1879) Begriffsschrift, English translation in J. van Heijenoort, ed. (1967) From Frege to Gödel, Cambridge, MA: Harvard University Press, pp. 1-82.
Gentzen, Gerhard (1935) Untersuchungen über das logische Schließen, translated as Investigations into logical deduction in The Collected Papers of Gerhard Gentzen, ed. and translated by M. E. Szabo, Amsterdam: North Holland, 1969, pp. 68-131.
Haas, Norman, & Gary G. Hendrix (1983) Learning by being told, in R. S. Michalski, J. G. Carbonell, & T. M. Mitchell, Machine Learning, Palo Alto: Tioga, pp. 405-427.
Hayek, Petr (2010) Fuzzy logic, Stanford Encyclopedia of Philosophy.
Hays, David G. (1964) Dependency theory: a formalism and some observations, Language 40(4), 511-525.
Hendler, James A. (1987) Integrating Marker Passing and Problem Solving, Hillsdale, NJ: Lawrence Erlbaum.
Hendler, James A. (1992) Massively-parallel marker-passing in semantic networks, in Lehmann (1992) pp. 277-291.
Hendler, James A., & Frank van Harmelen (2008) The Semantic Web: webizing knowledge representation, in van Harmelen et al. (2008) pp. 821-839.
Hendrix, Gary G. (1975) Expanding the utility of semantic networks through partitioning, in Proc. IJCAI-75, 115-121.
Hendrix, Gary G. (1979) Encoding knowledge in partitioned networks, in Findler (1979) pp. 51-92.
Hinton, Geoffrey A. (2013) Neural network tutorials, http://www.cs.toronto.edu/~hinton/nntut.html
Hoekstra, Rinke (2007) EL, http://www.w3.org/2007/OWL/wiki/EL
ISO/IEC (2007) Common Logic (CL) — A Framework for a family of Logic-Based Languages, IS 24707, Geneva: International Organisation for Standardisation.
Jain, Anil K., Jianchang Mao, & K Moidin Mohiuddin (1996) Artificial neural networks: a tutorial, IEEE Computer 29:3, 31-44.
Jensen, Kurt (1992) Coloured Petri Nets, vol. 1, Berlin: Springer.
Kamp, Hans (1981) Events, discourse representations, and temporal references, Langages 64, 39-64.
Kamp, Hans, & Uwe Reyle (1993) From Discourse to Logic, Dordrecht: Kluwer.
Kent, Stuart, Andy Evans, & Bernhard Rumpe, eds. (1999) UML Semantics FAQ, http://www.cs.ukc.ac.uk/pubs/1999/977/content.pdf
Klein, Sheldon, & Robert F. Simmons (1963) Syntactic dependence and the computer generation of coherent discourse, Mechanical Translation 7.
Kolodner, Janet L. (1993) Case-Based Reasoning, San Mateo, CA: Morgan Kaufmann.
Lendaris, George G. (1988a) Neural networks, potential assistants to knowledge engineers, Heuristics 1:2.
Lendaris, George G. (1988b) Conceptual graph knowledge systems as problem context for neural networks, Proc. ICNN-88, San Diego.
Levesque, Hector, & John Mylopoulos, A procedural semantics for semantic networks, in Findler (1979) pp. 93-120.
Levinson, Robert A. (1996) General game-playing and reinforcement learning, Computational Intelligence 12:1 155-176.
Maida, Anthony S., & Stuart C. Shapiro (1982) Intensional concepts in propositional semantic networks, Cognitive Science 6:4, 291-330.
Masterman, Margaret (1961) Semantic message detection for machine translation, using an interlingua, in NPL (1961) pp. 438-475.
McCulloch, Warren S., & Walter Pitts (1943) A logical calculus of the ideas immanent in nervous activity, Bulletin of Mathematical Biophysics 5, 115-133.
Mel'čuk, Igor A. (1973) Towards a linguistic 'Meaning ⇔ Text' model, in F. Kiefer, ed., Trends in Soviet Theoretical Linguistics, Dordrecht: Reidel, pp. 35-57.
Mylopoulos, John (1992) The PSN tribe, in Lehmann (1992) 223-241.
Navigli, Roberto, & Simone Paolo Ponzetto (2012) BabelNet: The automatic construction, evaluation and application of a wide-coverage multilingual semantic network, Artificial Intelligence 193, 217-250.
Newell, Allen, & Herbert A. Simon (1972) Human Problem Solving, Englewood Cliffs, NJ: Prentice Hall.
Object Management Group (2013) Semantics of a Foundational Subset for Executable UML Models (FUML), http://www.omg.org/spec/FUML/
Ockham, William of (1323) Summa Logicae, Paris: Johannes Higman, 1488. Part I translated as Ockham’s Theory of Terms by M. J. Loux, Notre Dame, IN: University Press. Part II translated as Ockham’s Theory of Propositions by A. J. Freddoso & H. Schuurman, Notre Dame, IN: University Press.
Peano, Giuseppe (1889) Aritmetices principia nova methoda exposita, Torino: Bocca. Excerpt translated as Principles of mathematics presented by a new method in van Heijenoort (1967) pp.83-97.
Peirce, Charles Sanders (1880) On the algebra of logic, American Journal of Mathematics 3, 15-57.
Peirce, Charles Sanders (1885) On the algebra of logic, American Journal of Mathematics 7, 180-202.
Peirce, Charles Sanders (1909) Manuscript 514. For excerpts and commentary see Sowa (2011).
Peppas, Pavlos (2008) Belief revision, in van Harmelen et al. (2008) pp. 317-359.
Peter of Spain or Petrus Hispanus (circa 1239) Summulae Logicales, edited by I. M. Bocheński, Turin: Marietti, 1947.
Porphyry, On Aristotle’s Categories, translated by S. K. Strange, Ithaca, NY: Cornell University Press, 1992.
Quillian, M. Ross (1966) Semantic Memory, PhD dissertation, Carnegie Institute of Technology (now CMU). Abridged version in Minsky (1968) pp. 227-270.
Rational Software (1997) UML Semantics, http://www.rational.com/media/uml/resources/media/ad970804_UML11_Semantics2.pdf
Richens, Richard H. (1956) Preprogramming for mechanical translation, Mechanical Translation 3:1, 20-25.
Rieger, Chuck (1976) An organization of knowledge for problem solving and language comprehension, Artificial Intelligence 7:2, 89-127.
Roberts, Don D. (1973) The Existential Graphs of Charles S. Peirce, The Hague: Mouton.
Rosenblatt, Frank (1958) The perceptron: a probabilistic model for information storage and organization in the brain, Psychological Review 65:6, 386-408.
Schank, Roger C., ed. (1975) Conceptual Information Processing, Amsterdam: North Holland.
Schank, Roger C. (1982) Dynamic Memory, New York: Cambridge University Press.
Schank, Roger C., & Larry G. Tesler (1969) A conceptual parser for natural language, Proc. IJCAI-69, 569-578.
Schank, Roger C., & Robert P. Abelson (1977) Scripts, Plans, Goals and Understanding, Hillsdale, NJ: Lawrence Erlbaum.
Schank, Roger C., Alex Kass, & Christopher K. Riesbeck (1994) Inside Case-Based Explanation, Hillsdale, NJ: Lawrence Erlbaum.
Shapiro, Stuart C. (1971) A net structure for semantic information storage, deduction and retrieval, Proc. IJCAI-71, 512-523.
Shapiro, Stuart C. (1979) The SNePS semantic network processing system, in Findler (1979) pp. 263-315.
Shapiro, Stuart C., & William J. Rapaport (1992) The SNePS family, in Lehmann (1992) pp. 243-275.
Selz, Otto (1913) Über die Gesetze des geordneten Denkverlaufs, Stuttgart: Spemann.
Selz, Otto (1922) Zur Psychologie des produktiven Denkens und des Irrtums, Bonn: Friedrich Cohen.
Simon, Herbert A. (1981) Otto Selz and information-processing psychology, in N. H. Frijda A. D. de Groot, eds., Otto Selz: His Contribution to Psychology, The Hague: Mouton.
Somers, Harold L. (1987) Valency and Case in Computational Linguistics, Edinburgh: University Press.
Sowa, John F. (1976) Conceptual graphs for a data base interface, IBM Journal of Research and Development 20:4, 336-357.
Sowa, John F. (1984) Conceptual Structures: Information Processing in Mind and Machine, Reading, MA: Addison-Wesley.
Sowa, John F. (2008) Conceptual graphs, in van Harmelen et al. (2008) pp. 213-237.
Sowa, John F. (2011) Peirce’s tutorial on existential graphs, Semiotica 186:1-4, 345-394.
Sowa, John F. (2013) From existential graphs to conceptual graphs, International Journal of Conceptual Structures 1:1, 39-72.
Steele, James, ed. (1990) Meaning-Text Theory, Ottawa: University Press.
Suzuki, Hideaki, Mikio Yoshida. & Hidefumi Sawai (2014) A network representation of first-order logic that uses token evolution for inference, Journal of Information Science and Engineering 30, 669-686.
Tesnière, Lucien (1959) Éléments de Syntaxe Structurale, corrected edition, Paris: Librairie C. Klincksieck, 1988. Translated as Elements of Structural Syntax by T. Osborne & S. Kahane, Amsterdam: John Benjamins, 2015.
Thorndike, Edward Lee (1932) The Fundamentals of Learning, New York: Teachers College Press.
Troelstra, Anne Sjerp (1992) Lectures on Linear Logic, Stanford, CA: CSLI.
Tulving, Endel (1972) Episodic and semantic memory, in E. Tulving & W. Donaldson, eds., Organization of Memory, New York: Academic Press.
Wilks, Yorick, & Dan Fass (1992) The preference semantics family, in Lehmann (1992) pp. 205-222.
Winston, Patrick Henry, (1975) Learning structural descriptions from examples, in P. H. Winston, ed., The Psychology of Computer Vision, New York: McGraw-Hill, pp. 157-209.
Woods, William A. (1975) What’s in a link: foundations for semantic networks, in D. G. Bobrow & A. Collins, eds. (1975) Representation and Understanding, New York: Academic Press, pp. 35-82.
Woods, William A., & James G. Schmolze (1992) The KL-ONE Family, in Lehmann (1992) pp. 133-177.
Wos, Larry (1988) Automated Reasoning: 33 Basic Research Problems, Englewood Cliffs, NJ: Prentice Hall.
Zadeh, Lotfi A. (1975) Fuzzy logic and approximate reasoning, Synthese 30, 407-428.
Send comments to John F. Sowa.
Last Modified: