
Figure 1: Positions from the games of go and go-moku
Systems, scientific and philosophic, come and go. Each method of limited understanding is at length exhausted. In its prime each system is a triumphant success: in its decay it is an obstructive nuisance.Alfred North Whitehead, Adventures of Ideas
Abstract. According to Heraclitus, panta rhei — everything is in flux. But what gives that flux its form is the logos — the words or signs that enable us to perceive patterns in the flux, remember them, talk about them, and take action upon them even while we ourselves are part of the flux we are acting in and on. Modern physics is essentially a theory of flux in which the ultimate building blocks of matter maintain some semblance of stability only because of conservation laws of energy, momentum, spin, charge, and more exotic notions like charm and strangeness. Meanwhile, the concepts of everyday life are derived from experience with objects and processes that are measured and classified by comparisons with the human body, its parts, and its typical movements. Yet despite the vast differences in sizes, speeds, and time scale, the languages and counting systems of our stone-age ancestors have been successfully adapted to describe, analyze, and predict the behavior of everything from subatomic particles to clusters of galaxies that span the universe. Any system of ontology that is adequate for defining the concepts used in natural languages must be at least as flexible as the languages themselves: it must be able to accommodate all the categories of thought that are humanly conceivable and relate them to all possible experiences, either directly by human senses or indirectly by whatever instrumentation any scientist or engineer may invent. As a foundation for such an ontology, this paper proposes the philosophies of three logicians who understood the limitations of logic in dealing with the both the flux and the logos: Charles Sanders Peirce, Alfred North Whitehead, and Ludwig Wittgenstein.
This is an extended version of an invited lecture presented in May 1999 at the International Conference on the Challenge of Pragmatic Process Philosophy at the University of Nijmegen. For a PDF version, click here.
The primary task of ontology, as it was practiced by its founder Aristotle, is to bridge the gap between what exists and the languages, both natural and artificial, for talking and reasoning about what exists. Aristotle did not state that goal explicitly, but it is the unifying theme exemplified in his life’s work: the analysis of the basic principles of every branch of knowledge and their organization in a system that shows how the diverse subjects are related to one another. Although Aristotle did not work out all the details himself, he laid the foundations for the science and technology of the Hellenistic era that followed him, the great flowering of Islamic civilization in the early middle ages, and the grand synthesis by the 13th century Scholastics in response to the clash of the Islamic, Jewish, and Christian cultures in Spain. In linguistics, the Scholastics developed Aristotle’s correspondence theory of truth into an early version of model-theoretic semantics, which they applied to the analysis and definition of the quantifiers and logical connectives of Latin. In fact, the Theory of Propositions by William of Ockham (1323) would still serve as a good introduction to model theory for linguists who are discouraged by Richard Montague’s formidable notation.
Today, the goal of developing an ontology that can support natural language processing and knowledge sharing among heterogeneous computer systems requires such a synthesis. Following are three systems with the largest hierarchies of categories, all of which are defined by Aristotle’s method of genus and differentiae:
Although Aristotle’s logic and categories still serve as a paradigm for the ontologies used in modern computer systems, his grand synthesis began to break down in the 16th century. Aristotle’s physics and cosmology were demolished by the work of Copernicus, Kepler, Galileo, and Newton. In philosophy, the skeptical tradition of antiquity was revived by the publication in 1562 of a new edition of the works of Sextus Empiricus, whose attacks on Aristotle were popularized by the essays of Michel de Montaigne (Annas & Barnes 1985). In responding to the skeptics, Descartes began his search for certainty from the standpoint of universal doubt, but he merely reinforced the corrosive effects of skepticism. The British empiricists responded with new approaches to epistemology, which culminated in Hume’s devastating criticisms of the foundations of science itself. Two responses to Hume helped to restore the legitimacy of science: Thomas Reid’s critical common sense and Immanuel Kant’s three major Critiques. Kant (1787) adopted Aristotle’s logic as the basis for his new system of categories, which he claimed would be sufficient for defining all other concepts:
If one has the original and primitive concepts, it is easy to add the derivative and subsidiary, and thus give a complete picture of the family tree of the pure understanding. Since at present, I am concerned not with the completeness of the system, but only with the principles to be followed, I leave this supplementary work for another occasion. It can easily be carried out with the aid of the ontological manuals. (A:82, B:108)Yet after two hundred years, Kant’s easy task is still unfinished. His Opus postumum records the struggles of the last decade of his life when Kant tried to make the transition from his a priori metaphysics to the experimental evidence of physics. Förster (2000) wrote “although Kant began this manuscript in order to solve a comparatively minor problem within his philosophy, his reflections soon forced him to readdress virtually all the key problems of his critical philosophy: the objective validity of the categories, the dynamical theory of matter, the nature of space and time, the refutation of idealism, the theory of the self and its agency, the question of living organisms, the doctrine of practical postulates and the idea of God, the unity of theoretical and practical reason, and, finally, the idea of transcendental philosophy itself.”
Before attempting a new synthesis, it is important to understand the strengths and weaknesses of the Aristotelian achievement and the lessons that can be learned from it. What, if anything, can be salvaged from it? What philosophical foundations might be better able to accommodate the breakthroughs in modern science, logic, linguistics, and computer science? What semantic foundations could support the highly technical languages of science, the colloquial speech of everyday life, and the problems of finding, sharing, and reasoning with knowledge scattered among millions of computers across the Internet? Should Kant’s achievements be considered an encouraging step toward a new synthesis or a discouraging dead end?
Those questions were raised and answered by Peirce, Whitehead, and Wittgenstein — three logicians who understood the limitations of logic when applied to the problems of language and life. What set them apart from their contemporaries was their willingness to build the foundations of their philosophies on the recognition that logic, although important, is limited in what it can do. Section 2 of this paper reviews the difficulties encountered by the 20th-century analytic philosophers who either failed to recognize the limitations of logic or tried to bury their doubts under many layers of formalism. Section 3 analyzes the efforts in artificial intelligence to design logical systems that can cope with the limitations of logic. Sections 4, 5, and 6 show how Peirce, Whitehead, and Wittgenstein developed methods for accommodating the limitations, not eliminating them. Finally, Section 7 outlines the proposed new foundations: Whitehead’s process philosophy as a theory of the flux, Peirce’s semiotics as a theory of the logos, and Wittgenstein’s language games as a theory of semantic change and adaptability. Together, they provide a foundation for ontology that is capable of any desired level of precision, while accommodating the inevitable discrepancies that occur when discrete symbols are used to approximate a continuous world.
Using logic as a tool for knowledge representation is the chief characteristic of analytic philosophy. It began in a revolutionary spirit, which is most clearly defined by what it rejected. The founder, Gottlob Frege (1879), set out “to break the domination of the word over the human spirit by laying bare the misconceptions that through the use of language often almost unavoidably arise concerning the relations between concepts.” Bertrand Russell shared Frege’s contempt for natural language and sought refuge in a purified language of logic. The theory of logical atomism, which Russell (1918) developed in partnership with Ludwig Wittgenstein, was a natural outgrowth: predicate calculus has only two quantifiers, which range over a discrete set of individuals; therefore, the world should be describable by a logical combination of atomic facts about discrete atoms. The major achievements of analytic philosophy resulted from the application of symbolic logic to the analysis of language and the description of the world. Its major weaknesses stemmed from that same source. It focused on those aspects of language and the world that were easy to represent in logic. Unfortunately, everything else was systematically ignored — especially human purposes, intentions, society, and life.
To eliminate metaphysical assumptions, Russell (1924) formulated what he called “the supreme axiom in scientific philosophising”: “Whenever possible, substitute constructions out of known entities for inferences to unknown entities” (p. 363). Among scientists, the behaviorists were the most enthusiastic in purging their theories of all traces of unobservable mental notions. They even dropped the name psychology because it implied an unobservable psyche. Physicists, however, ignored Russell’s supreme axiom and happily constructed theories about unobservable fields, forces, particles, and waves. Albert Einstein (1944) criticized Russell’s “fear of metaphysics” (Angst vor der Metaphysik) as a “malady (Krankheit) of 20th-century empirical philosophy.” Contrary to Russell, Einstein maintained that “the concepts which arise in our thought and in our linguistic expressions are all — logically considered — free creations of thought which cannot be inductively derived from sense experiences.” He believed that was just as true “for everyday thinking as for the more consciously and systematically developed thought in the sciences.”
Russell and Wittgenstein had a strong influence on the Vienna Circle, including Rudolf Carnap, who had been one of Frege’s few students. The Vienna Circle combined the positivism of an earlier Viennese, Ernst Mach, with the new language of logic to form logical positivism, whose primary thesis was the rejection of metaphysics and any theoretical terms that could not be explicitly defined in terms of observable data. To this mix, a visitor to the Vienna Circle, Alfred Tarski (1933, 1936) contributed model-theoretic semantics, which gave a formal definition of the truth of compound statements in terms of elementary facts about individuals. Tarski’s combining rules for deriving the truth value of a compound sentence from its elementary clauses were equivalent to Ockham’s. What was novel was the rejection of any aspect of meaning that could not be reduced to relations of individual objects.
Among the major achievements of analytic philosophy were Der Logische Aufbau der Welt by Rudolf Carnap (1928) and The Structure of Appearance by Nelson Goodman (1951). Both authors used symbolic logic to “construct” a description of the world in terms of observable entities. Carnap took the more challenging approach of reducing everything to primitive sensory data, which he called Elementarerlebnisse (elementary experiences). He showed how to use logic, set theory, and geometry to define physical objects in terms of sensory data. Goodman took an easier, but quicker approach by starting with physical objects and using mereology to combine them in larger structures. In both books, the primary emphasis was on the representation of static physical objects. For Carnap, psychological “objects” are physical objects that have a spatiotemporal location within an individual human object (§18). Carnap “clarified” the notion of intention relation by saying it is “nothing but” a relation between a psychological object and some other object (§164). Carnap recognized the importance of the sign relation and admitted “The construction of this relation is more difficult than any of the other relations which we have hitherto undertaken” (§141). In his later works, Carnap (1934, 1947, 1954) returned to the problems of representing signs, but only in formal languages. Richard Montague (1970) combined Carnap’s approach with Kripke’s model theory to develop a formal semantics for a 37-word “fragment” of English.
Analytic philosophy was criticized throughout the 20th century by philosophers who were partisans of other traditions. But the most serious criticisms were formulated by its own adherents or by philosophers who had been closely associated with the founders. Although Peirce invented the notation for logic that the logical positivists adopted, he had been a harsh critic of the attempt to eliminate metaphysics by the 19th-century positivists, Auguste Comte (1830) and Ernst Mach (1886). His criticism applies equally well to the logical positivists: “Find a scientific man who proposes to get along without any metaphysics... and you have found one whose doctrines are thoroughly vitiated by the crude and uncriticized metaphysics with which they are packed” (CP 1.129). As an example of the vitiating effect of his crude metaphysics, Mach fought a long, desperate battle against the assumption of unobservable atoms. He prevented his fellow Viennese, Ludwig Boltzmann, from receiving proper recognition for his brilliant theory of statistical mechanics (Lindley 2001). Einstein was even more blunt: “Mach was a good experimental physicist but a miserable philosopher”; he made “a catalog not a system” (quoted by Lindley, p. 219).
The most devastating criticism, which analytic philosophers have never been able to answer, was by Wittgenstein. In his first book, Wittgenstein (1922) presented the clearest formulation of logical atomism, which he and Russell had jointly developed before World War I. In his second book, however, Wittgenstein (1953) repudiated the “grave mistakes” in “what logicians have said about the structure of language,” among whom he included Frege, Russell, and his earlier self. Instead of his direct mapping from language to the world, which was highly compatible with Tarski’s model theory, Wittgenstein later developed the theory of language games, which are linguistically far more realistic, but far more difficult to reconcile with analytic philosophy.
Although Whitehead coauthored the Principia Mathematica with Russell, he was highly critical of Russell’s approach to philosophy and rejected nearly all the basic assumptions of analytic philosophy. Whereas Russell emphasized static relations among things, Whitehead presented a dynamic theory of processes. Whereas Russell tried to avoid metaphysical entities, Whitehead boldly posited Platonic Forms, which he called eternal objects. Whereas Russell believed in absolute clarity, Whitehead (1937) maintained “In the focus of experience, there is comparative clarity. But the discrimination of this clarity leads into the penumbral background. There are always questions left over.” When introducing Russell for his William James Lectures at Harvard, Whitehead said “This is my friend Bertrand Russell. Bertie thinks that I am muddleheaded, but then I think that he is simpleminded” (Lucas 1989:111). That remark is consistent with a statement attributed to Russell: “I’d rather be narrow minded than vague and wooly” (Kuntz 1984:50).
Another analytic philosopher, Nicholas Rescher, had a broad background in other traditions, including Arabic and medieval philosophy. While reviewing Quine’s Word and Object, he was struck by the absence of any discussion of events, processes, actions, and change. After reviewing the literature, Rescher (1962) realized that Quine’s static views were endemic in the tradition: “The ontological doctrine whose too readily granted credentials I propose to revoke consists of several connected tenets, the first fundamental, the rest derivative:”
Rescher found that the only analytic philosopher who bothered to defend the static view was Peter Strawson (1959), who claimed that “identifiability” and “independence” were sufficient criteria for ontological priority: “whether there is reason to suppose that identification of particulars belonging to some categories is in fact dependent on the identification of particulars belonging to others, and whether there is any category of particulars that is basic in this respect” (pp. 40-41). By applying that principle, Strawson concluded that physical objects are ontologically basic because processes cannot be identified without first identifying the objects that participate in them. Rescher, however, found Strawson’s arguments unconvincing and presented three rebuttals, which can be summarized briefly:
The thing-property ontology, which Russell (1918) pushed to the extreme of treating objects as nothing but “a bundle of properties,” is derived from the substance-property-accident representation of Aristotle’s early philosophy. In reviewing the development of Greek philosophy, Wolfgang-Rainer Mann (2000) observed that far from being common sense, the position Aristotle presented in the Categories was “a revolutionary metaphysical picture”:
To formulate it most starkly: before the Categories and Topics, there were no things. Less starkly, things did not show up as things, until Aristotle wrote those two works. (p. 4)The fundamental issue is the nature of the ‘beings’ or ‘entities’ (ta onta) that are ontologically primary. Both Plato and Aristotle used the word ousia for those privileged entities. Plato considered the abstract Forms to be ousiai and physical entities to be imperfect copies that participate in the Forms. In the Categories, however, Aristotle considered physical things, of which his main examples were living things, to be ousiai, which Boethius translated into Latin as substantiae. But as Mann notes, Aristotle distanced himself from those early views in his later philosophy, especially the Metaphysics and De Anima. In those books, Aristotle’s primary representation of physical entities is the form-matter composite, which is more compatible with Plato than with his own early philosophy. The main difference between Plato and the later Aristotle is over the nature of the combination: whether physical entities participate in the Forms or whether the Forms inhere in the physical entities.
Besides telling a fascinating story about the development of ancient philosophy, Mann raised serious questions about what views might be considered “common sense.” He also observed that the presocratic philosophers had no single word that corresponds to the English word thing. The closest words in Greek were derived from verbs: pragma literally means what is done, and chrêma means what is used. Other languages also use verbal forms for “object”: objectus in Latin and Gegenstand in German mean something that is thrown against or standing in the way. As Mann’s analysis indicates, a revolutionary view that Aristotle once proposed and later abandoned can hardly be considered so obvious that no further justification is required.
During the course of the 20th century, many philosophers who were trained in the analytic tradition broadened their views in order to deal with human language, intentions, and society. Among them are John Searle (1969, 1982, 1995), who wrote several books on those subjects, Michael Bratman (1987), whose theory of beliefs, desires, and intentions has been formalized and applied to AI systems called BDI agents, and Barwise and Perry (1983), whose work on situation semantics has been influential in formal theories of propositional attitudes. In psychology, strict behaviorism began to decline with the publication of Edward Tolman’s (1948) classic paper, “Cognitive Maps in Rats and Men.” In that paper, Tolman showed that the behavior of rats running a maze cannot be adequately explained without assuming that they form a mental map of the maze in their brains. Thirty years later, O’Keefe and Nadel (1979) showed that the hippocampus is involved in building cognitive maps, and later evidence from neural imaging experiments provided further confirmation. In short, cognitive psychology has demonstrated that mental hypotheses are worthy of serious scientific study, neural evidence shows they are correlated with observable activity in the brain, and AI researchers collaborating with philosophers, linguists, and psychologists have formalized those hypotheses and implemented them in working computer systems.
Despite the growing acceptance of mental hypotheses in cognitive science, some philosophers have continued to observe Russell’s supreme axiom. One example is Barry Smith (1995, 1998, 1999), who has struggled to eliminate mental notions by defining all aspects of human life in terms of mereological sums of physical objects and processes. His resulting ontology has two basic categories, continuants (physical objects) and occurrents (processes), which can be combined by mereology to form complex entities called physical-behavioral units and social objects:
As this discussion indicates, analytic philosophy was “a triumphant success” at the beginning of the 20th century, but it became, in Whitehead’s terms, “an obstructive nuisance” by the end of the century. In the early days, it served a useful purpose by promoting the development of logic as a tool for knowledge analysis and representation. Its weaknesses, however, resulted from the prejudices of its founders: Frege and Russell tried to replace natural languages with logic; Carnap, Neurath, and Hahn (1929) published a manifesto denouncing metaphysics; and Russell’s “supreme axiom” excluded the most difficult and important problems from “scientific philosophizing.” To bring those problems back into the province of science and philosophy, Frege’s slogan should be turned on its head:
We must break the domination of analytic philosophy over the human spirit by laying bare the misconceptions that through ignorance of goals, purposes, and intentions unavoidably arise concerning the relations of agents, concepts, and the world.
AI researchers are divided in two camps: the “scruffies” reject logic because of its limitations, and the “neats” try to apply logic along the lines advocated by analytic philosophers. One of the early successes of AI, the SHRDLU system by Terry Winograd (1972), was a classic implementation of the neat approach: it combined Russell’s logical atomism with a Fregean compositional semantics, a Tarskian model theory, and a version of speech acts (Austin 1962). As an example, following is SHRDLU’s response to a command:
(goal (and (is ?X1 Block)
(is ?X2 Pyramid)
(support ?X1 ?X2)))
U: Are there any steeples? S: Sorry, I don’t know the word “steeple”. U: A “steeple” is a stack which contains two green cubes and a pyramid. S: I understand. U: Are there any steeples now? S: No. U: Build one. S: OK.SHRDLU was freely distributed across Arpanet, and many people tried to use its extensibility features to build ontologies for new domains, but without much success. The following dialog illustrates the difficulties:
U: I’ll trade you a squirtgun for a big red block. S: Sorry, I don’t know the word “trade”. U: A “trade” is a free exchange of property. S: Sorry, I don’t know the word “free”. U: A “free” act is done willingly, without being forced. S: Sorry, I don’t know the word “act”. U: “acts” are what people do on purpose and not by accident. S: Sorry, I don’t know the word “people”. U: Sorry, I thought you were smarter than you are. S: Sorry, I don’t know the word “sorry”.
The title of Winograd’s book, Understanding Natural Language, was an exaggeration, which he recognized when he tried to extend SHRDLU to a broader coverage of language use. After some discussions with the phenomenologist Hubert Dreyfus, Winograd abandoned his earlier approach and adopted its diametric opposite, the phenomenology of Martin Heidegger. In their later book, Winograd and Flores (1986) explained the weaknesses of the SHRDLU approach: it makes no room for context, background, social commitment, discussion, negotiation, and the inevitable exceptions that cause a fragile formal system to break down. Since those issues were ruled outside the bounds of scientific philosophy by Frege, Russell, and Carnap, it’s not surprising that Winograd should turn to Heidegger, their most vociferous opponent.
SHRDLU was considered a success in 1972 and a failure in 1980, but it was an interesting failure from which a great deal has been learned. Like many AI systems, SHRDLU implemented a limited version of intentionality. Each input or output statement could be represented as a pair (p,m), in which p is a proposition, and m is a marker that indicates the intended speech act, such as assertion, question, answer, command, definition, warning, or apology. To answer a question or obey a command, SHRDLU would derive a top-level purpose or goal. Then it would break that goal into multiple subgoals, which could be further subdivided into lower-level subgoals. If a subgoal failed, SHRDLU would try an alternative or ask for help. If the top-level goal failed, SHRDLU would apologize. That level of intentionality, although not very sophisticated, demonstrates that intentions can be formalized and analyzed with the same kind of logic used to represent observables.
Although intentions themselves are not directly observable, they may have observable effects. The most clearly visible effects result from activities, such as planning, problem solving, or game playing, which are directed toward some goal under the influence of certain constraints. As an example, Figure 1 shows two patterns that occurred during the play of the Japanese games of go and go-moku. Both games use the same board, the same pieces, and the same syntactic rules for making legal moves: the board is lined with a 19 by 19 grid; the pieces consist of black stones and white stones; and two players start with an empty board and take turns in placing stones on the intersections of the grid. A position from the game of go is on the left of Figure 1, and a position from go-moku is on the right.

Figure 1: Positions from the games of go and go-moku
The most striking difference between the two board positions is that the go pieces are scattered around the edges, and the go-moku pieces are clustered in the middle. At a purely syntactic level, either position is legal in either game. But the intention of winning the game causes every move to be evaluated in terms of its potential effect on the final score, which is not computed until the end of the game. In go, the score is determined by the amount of territory each player has surrounded; therefore, the stones are viewed as competing “armies” that stand guard over their territory. In go-moku, the winner is the first player who forms a straight line with five stones of the same color; therefore, go-moku stones are placed in the middle, where they can form connected lines or block the opponent’s lines. Intentionality is most easily formalized in game programs, but its effects are just as visible in anything that results from design and planning: buildings, highways, airplanes, orchestras, armies, businesses, and governments.
In computing the effects of intentions, AI systems routinely quantify and refer to events, potential events, and possible futures in ways that Strawson would not approve. To illustrate Davidson’s event semantics, Strawson (1992) claimed that the sentence John kissed Mary in the garden at midnight would require a complex representation such as the following formula:
(∃e)(∃g)(∃t) (kiss(e) ∧ garden(g) ∧ midnight(t) ∧ agent(e,John) ∧ theme(e,Mary) ∧ location(e,g) ∧ pointInTime(e,t)).In an attempt to discredit Davidson’s proposal, Strawson complained about the complexity of such formulas. As an alternative, he argued “What could be more simple and straightforward than the idea of a construction whereby we may tack on to the verbs of happening or action in such sentences a phrase which answers these when? and where? questions” (p. 104). Notations that “tack on” such qualifiers have long been used in AI; as an example, Figure 2 is a representation of Strawson’s sentence as a conceptual graph (Sowa 1984, 2000).

Figure 2: A simpler representation of Strawson’s sentence
Figure 2 satisfies Strawson’s criteria of simplicity, but it is a formal notation that is that is logically equivalent to Davidson’s. Each box in Figure 2, which is called a concept, has an implicit existential quantifier. Each circle, which is called a conceptual relation, can be translated to a predicate, such as loc(e,g) or pTim(e,t). Although no one knows exactly what kind of representations occur in the human brain, Strawson is correct in saying that a graph-like connection is more likely than a formula in predicate calculus. But Figure 2 shows that graphs can express the equivalent information with Strawson’s desired level of simplicity.
Model-theoretic methods for evaluating truth are most convenient when the elementary data can be stored in the tables of a relational database. They can also be adapted to simulated robots such as SHRDLU that have been designed to extract the equivalent information dynamically. As an example, consider the following command to SHRDLU:
This statement, which avoids all detail about how the block is manipulated and carried, has the same necessary and sufficient conditions for a human arm or a robot arm:Move Block X from A to B.
Model theory breaks down when the high-level abstractions are “embodied” in the detailed motions of an animal or a robot. The arm must be transported from an arbitrary starting position to point A; its grasping mechanism must be aligned with the block; the grasp must be sufficiently tight to hold the block firmly, but without crushing it; the arm with the block must be moved to B, avoiding obstacles that might obstruct any part of the arm or the block; the motion must be stopped before the bottom of the block reaches the surface at B; the approach to the surface must be slow enough to avoid breaking the block or the supporting material; and finally, the grasp must be released. These detailed statements use verbs like grasp, hold, crush, avoid, obstruct, reach, approach, break, and release, whose truth conditions require information from sensors that are continuously monitoring the arm, the block, and the environment. Model theory, as defined by Tarski and extended by Kripke, Montague, and others, was never designed to accommodate dynamic information about interacting agents in a complex environment.
The weakness of model theory is not in the Ockham-Tarski combining rules for compound sentences, but in the methods for evaluating the truth of the elementary clauses. As an alternative, Lakoff and Johnson (1999) rejected neat approaches based on logic and advocated scruffy methods. Their work is part of a project called the Neural Theory of Language (NTL), which is being developed by Jerome Feldman, George Lakoff, Lokendra Shastri, and their students. As examples, the NTL group has undertaken several major tasks in language understanding and learning:
By showing the importance of the human motor and perceptual mechanisms for understanding verbs and spatial relations, these projects give concrete meaning to the catchphrase embodied mind. The “neural” metaphor, however, is not entirely justified, since the mechanisms that support these systems use conventional computations. Jack is based on methods used in virtual reality, Petri nets are a distributed-processing method commonly used to simulate multithreaded operating systems, and PDP networks are statistical computing systems that have only a remote resemblance to actual neurons. A more appropriate acronym might be VRTL, for Virtual Reality Theory of Language.
The possible motions of the bones and joints determine much more detailed, dynamic conditions for truth than the static relations of a traditional Tarski-style model. Imagine, for example, a basketball player shooting a ball through a hoop while running, jumping, and trying to avoid other players who are also running, jumping, and waving their arms in an attempt to obstruct the trajectory of the ball. Although the trajectories may be computable, the patterns of relationships are not given in advance, and they cannot be computed without modeling the three-dimensional interactions of multiple moving objects. Even slower interactions of just two objects may require considerable background knowledge. Consider how a human being or a computer might evaluate the truth conditions for the following sentences:
In summary, the only thing analytic philosophy has to offer is something AI already has in abundance: elegant formal techniques. In analyzing and representing knowledge about the world, AI researchers have been forced to address problems that analytic philosophers have deliberately ignored:
Peirce was no armchair philosopher. He published research in chemistry, astronomy, physics, mathematics, and logic. During the late 19th century, he had an international reputation as the leading expert both in symbolic logic and in methods of measuring gravity. Among his other achievements, he was the first person to propose a wavelength of light as a standard for length, and he demonstrated its practicality by designing the equipment for using light waves to measure the length of the pendulums he used to measure gravity. Independently of Frege, Peirce created the modern algebraic notation for logic, which Peano modified by replacing Peirce’s symbols with special characters like ∃ and ∧. Unlike Frege and Russell, who sought to replace natural languages with logic, Peirce used logic as a tool for understanding language. In a letter to B. E. Smith, the editor of the Century Dictionary, Peirce wrote
The task of classifying all the words of language, or what’s the same thing, all the ideas that seek expression, is the most stupendous of logical tasks. Anybody but the most accomplished logician must break down in it utterly; and even for the strongest man, it is the severest possible tax on the logical equipment and faculty.Peirce spoke as an associate editor of that dictionary, for which he wrote, revised, or edited over 16,000 definitions. With his background in language, logic, and mathematics, Peirce knew how to define words, write axioms, and prove theorems. With his background in science and engineering, he knew how to verify hypotheses by experiments and how to design artifacts that satisfy requirements.
In philosophy, Peirce was a voracious reader who studied all the philosophers from ancient Greece to 19th-century Europe. Unlike most of his contemporaries, he was especially well versed in medieval philosophy and logic. He once boasted that he had the largest collection of medieval books on logic in Cambridge (which included the Harvard libraries). In his lectures of 1898, he said that in his youth he had been “a passionate devotee of Kant”:
I believed more implicitly in the two tables of the Functions of Judgment and the Categories than if they had been brought down from Sinai.... But Kant, as you may remember, calls attention to sundry relations between one category and another. I detected some additional relations between those categories, all but forming a regular system, yet not quite so. Those relations seemed to point to some larger list of conceptions in which they might form a regular system of relationship. After puzzling over these matters very diligently for about two years, I rose at length from the problem certain that there was something wrong with Kant’s formal logic.What was puzzling to Peirce, as it was to Hegel and many others, was the underlying principle for deriving the categories. Starting with the four major groups Quantity, Quality, Relation, and Modality, Kant divided each group into triads in order to derive twelve categories. As an example, Kant divided the group of relations into three categories named Inherence, Causality, and Community. Peirce noticed that Inherence could be defined by a monadic predicate that characterizes something by what it has in itself, independent of anything else; Causality would require a dyadic predicate that characterizes some reaction between two entities; and Community would depend on a triadic relation that establishes new connections among the members of the community. Following is Peirce’s summary of the principle:
First is the conception of being or existing independent of anything else. Second is the conception of being relative to, the conception of reaction with, something else. Third is the conception of mediation, whereby a first and a second are brought into relation. (1891)
Peirce’s trichotomy of Firstness, Secondness, and Thirdness is a metalevel principle that can be applied repeatedly to generate new categories. His first application was to analyze Kant’s method of subdividing his four major groups, but he later applied it to any method of conceiving anything.
Throughout all these activities, Peirce viewed semiotics or as he spelled it, semeiotic, as the unifying theme that relates naturally occurring signs and conventional symbols to concepts and reality: language, logic, and science are systems for manipulating signs to represent relationships in and about the world. In classifying signs, Peirce used his trichotomy to subdivide the sign relation into the triad of icon, index and symbol: an icon represents an object by its inherent form, which resembles the intended object; an index represents its object by some causal relationship, such as a pointing finger, a weather vane, or a dial on a meter; and a symbol represents its object by a convention established by some community. By repeatedly applying the trichotomy to sign types, analyzing their interrelationships, and eliminating types that are ruled out by other constraints, Peirce showed how three trichotomies of signs would generate ten types of signs. He later extended the analysis to show how ten trichotomies would generate 66 types of signs.
Besides using the trichotomies to classify signs, Peirce also used them to classify mathematics, philosophy, science, and the study of signs themselves. He subdivided the field of semiotics into three subfields according to which aspect of signs is addressed by each:
Charles Morris (1946) popularized Peirce’s classification under the headings syntax, semantics, and pragmatics. Unfortunately, Morris’s choice of words has led to confusion, especially over the word semantics, which logicians use in much same sense as Peirce’s term critical logic, but linguists use in a much broader sense. As an alternative, linguists have coined the term lexical semantics, which includes aspects of all three of Peirce’s branches.
Peirce also applied his trichotomy to subdivide these subfields. In analyzing the methods of reasoning, he observed that induction exemplifies Secondness because it depends on a dyadic relation between propositions and reality. Deduction exemplifies Thirdness because it is determined by mediating laws that relate premises to conclusions. In looking for the missing Firstness, he discovered the principle of abduction, which generates new hypotheses, which are further tested by the methods of deduction and induction. The AI methods of heuristics (which Peirce spelled heuretic) are special cases of abduction.
The principle of searching for the missing third is a valuable heuristic (or heuretic) for developing ontological categories. Peirce’s major criticism of the 19th century positivists was their failure to go beyond Secondness. That is also the major weakness of 20th century analytic philosophers. Following is a short list of the kinds of Thirdness they have either systematically ignored or failed to appreciate:
Causality, Interaction, Communication, Planning, Intention, Agency, Duty, Responsibility, Obligation, Authorization, Penalty, Permission, Organization, Strategy, Business, Society, Life.In commenting on life, Peirce observed “The problem of how genuine triadic relationships first arose in the world is a better, because more definite, formulation of the problem of how life first came about” (CP 6.332). In every living being, from bacteria to humans and perhaps beyond, semiosis is the crucial Thirdness that enables the organism to respond to signs by taking actions that serve to further its goals of getting food, avoiding harm, and reproducing its kind. For most life forms, those goals are unconscious, and most of them are built into their genes. But there is no difference in principle between the evolutionary learning that is encoded in genes and the individual learning that is encoded in neurons. Understanding life at every level and in every kind of organization from colonies of bacteria to human businesses and governments requires an understanding of signs, goals, communication, cooperation, and competition — all of which involve aspects of Thirdness.
The best way to appreciate the power of Peirce’s trichotomy is to use it to analyze problems that are difficult to solve or even state without them. One problem is the classification of verbs according to what aspect is signified: some directly observable event (Firstness); some indirectly related effects (Secondness); or the agent’s intentions (Thirdness). The next three sentences describe the same act in each of those ways:
Many of the problems analytic philosophers have either ignored or debated without reaching a satisfactory conclusion could have been solved by an application of Peirce’s semiotics. A typical example, which Russell (1905) thought he solved, is the problem of dealing with terms whose referents are nonexistent:
The present king of France is bald.People who had never studied philosophy would say that the phrase the present king of France has a meaning, even though no such person now exists. By his supreme axiom, however, Russell sought to replace unobservable entities, such as meaning, with observable signs that have observable referents. His solution was to paraphrase the sentence in a way that would enable its truth to be evaluated without raising questions of meaning:
There is one and only one present king of France, and that one is bald.Since the first conjunct is false, the entire sentence must be false, and the second conjunct can be ignored. The entire procedure can therefore be evaluated without attributing a “meaning” to terms that have no existing referents. Many people, including philosophers who wanted to avoid mental entities, felt there was something deeply unsatisfying about a solution that treated such terms as meaningless. Strawson (1950) tried to interpret the sentence in terms of English speakers’ habitual usage, and Russell (1969) responded by reasserting a preference for his original approach. Meanwhile, Carnap (1947), Donellan (1966), and Kripke (1977) proposed different ways of interpreting the sentence without admitting mental entities. In his conclusion, Kripke said that a complete treatment of definite descriptions should “make it clear why the same construction with a definite article is used for a wide range of uses.” But he admitted “I have not yet worked out a complete account that satisfies me.”
In commenting on the endless debates about the present king of France, Sharon Kaye (1997) observed that William of Ockham’s solution to the problems of nonexistent entities was logically equivalent to Russell’s, but it was general enough to handle the criticisms by Strawson and others. Following Aristotle and earlier Scholastic logicians, Ockham considered logical terms that may be written, spoken, or conceived:
A written term is part of a proposition written on some physical object, which is seen or can be seen by the bodily eye. A spoken term is part of a proposition spoken by the mouth and able to be heard by the bodily ear. A conceived term is an intention or passion of the soul naturally signifying or consignifying something and suited to be part of a mental proposition and to supposit for that which it signifies. (T, ch. 1)Peirce considered these three kinds of terms, including mental terms, to be special cases of signs. Another Scholastic distinction, which Peirce adopted and generalized, was the distinction between the significatio of a term and its suppositio or what it stands for. For comparison, following is a definition of sign by Peirce:
A sign, or representamen, is something which stands to somebody for something in some respect or capacity. It addresses somebody, that is, creates in the mind of that person an equivalent sign, or perhaps a more developed sign. That sign which it creates I call the interpretant of the first sign. The sign stands for something, its object. It stands for that object, not in all respects, but in reference to a sort of idea, which I have sometimes called the ground of the representamen. (CP 2.228)In Peirce’s terminology, the significatio of a term corresponds to its interpretant, and the suppositio of a term corresponds to its object. Frege made a similar distinction: the Sinn of a sign (Zeichen) is its significatio, and the Bedeutung of a sign is its suppositio. Following is Ockham’s definition:
Suppositio means taking the position of something else. Thus when a term in a proposition stands for something, in such a way that we use the term for the thing, and that the term (or its nominative case, if it occurs in an oblique case) is true of the thing (or of a demonstrative pronoun which points to the thing), then we say that the term supposits for the thing. This is true, at least, when the suppositing term is taken significatively. (T, ch. 63)Ockham’s definition accommodates the supposito of proper names, common nouns, and pointing words, which Peirce called indexicals. Peirce generalized the Scholastic distinctions and incorporated them into his classification of signs and signs of signs. Frege, however, never attained the breadth and depth of Ockham, let alone Peirce.
After presenting his theory of terms, Ockham applied it to the analysis of propositions. He started with simple propositions, consisting of a single subject and predicate, and continued with compound propositions. He formulated rules, which are logically equivalent to Tarski’s, for deriving the truth values of compound propositions from the truth or falsity of the simple propositions contained in them. Ockham actually went beyond Tarski in analyzing modal, temporal, and fictional propositions. To analyze propositions about figments and negated terms, Ockham used paraphrases in Latin that were logically equivalent to Russell’s paraphrases in symbolic logic. Following are two of his examples (P, ch. 12):
A donkey is a non-man. ⇒Ockham maintained that the first proposition is true because both parts of the conjunction are true. The second proposition is false because the first conjunct is false, and the second is therefore irrelevant to the truth value. Applying Ockham’s method to Russell’s sentence would produce the following paraphrase:
A donkey is something, and that is not a man.A chimera is a non-man. ⇒
A chimera is something, and that is not a man.
The present king of France is something, and that is bald.In 1323, the first conjunct would have been true, and the truth of the second conjunct would depend on historical evidence about Charles IV. As Kaye pointed out, Ockham’s solution, although equivalent to Russell’s, had the advantage of assigning a meaning to each term, even in the case of fictional entities.
Unlike Frege and his followers, Peirce not only studied the medieval logicians, he delivered several lectures at Harvard on the logic of both Duns Scotus and William of Ockham, two of the last and greatest of the Scholastics. Where they disagreed, he usually preferred the realism of Scotus to the nominalism of Ockham. But he learned from both and incorporated their insights into his own broader and deeper theory of signs. Following is a brief summary of his theory of indexicals:
As late as 1989, a group of 17 philosophers paid tribute to David Kaplan’s analysis of demonstratives and indexicals, while discussing Frege’s brief remarks on those topics in excruciating detail (Almog et al. 1989). None of them, however, mentioned Peirce or Ockham. In the concluding article of that collection, Kaplan (1989) admitted that he was not able to correct all the shortcomings of his earlier work: “I don’t know exactly how to fix some of the sections that now seem wrong, and I don’t yet see how to connect my current thinking, about propositional attitudes and proper names, with indexicals.” In the writings of the last two decades of his life, Peirce achieved a wide-ranging synthesis of his thoughts in these areas, where Kripke, Kaplan, and others admit that their ideas are still tentative or incomplete. Perhaps they wouldn’t agree with all of Peirce’s conclusions, but they cannot afford to ignore them.
Even more recently, Barry Smith and John Searle debated some issues, or rather talked past one another about some topics, which could have been clarified by an application Peirce’s trichotomy (Smith & Searle 2001). Smith began with a criticism of Searle’s book The Construction of Social Reality, which he tried to interpret in terms of his own ontology of social objects. Searle replied
I think in the end he makes many useful points, but I also believe that he misunderstands me in certain very profound ways. I believe his misunderstandings derive from the fact that he approaches this topic with a set of concerns that are fundamentally different from mine, and in consequence, he tends to take my views as attempts to answer his questions rather than attempts to answer my questions.In Peircean terms, Smith was trying to use the dyadic partOf relation of mereology to represent fundamentally triadic relations of people, social institutions, and their purposes. Searle, however, recognized the need for a triadic relation, which he expressed in the pattern X counts as Y in context C. This relation gave Searle greater flexibility than Smith’s dyads, but Smith criticized that flexibility as too loose and imprecise. In particular, Smith noted that a context itself is a social object that requires some independent definition. Both authors made valid points: Searle’s book illustrates the power of triadic relations for analyzing social institutions, but Smith’s criticism shows the need for greater precision in distinguishing different kinds of triads. Peirce’s trichotomy is the key to resolving this dispute: instead of using a single triad, Peirce formulated a metalevel principle for generating different triads when applied to different phenomena.
When applied to the modes of existence, Peirce’s trichotomy generates three fundamental ontological categories, which correspond to Kant’s triad under Modality: Possibility, Actuality, and Necessity.
Peirce’s category of signs overlaps the categories of modality because every sign is a way of interpreting something that is possible, actual, or necessary. In fact, everything that exists can be interpreted as a sign in many different ways. The most basic interpretation is what Peirce called a sinsign — something that serves as a sign of its own existence. A weather vane on a steeple, for example, is a sinsign when it is considered as a sign of itself. It serves as an index when it is used to indicate the direction of the wind. An icon of a rooster on the weather vane is a sign of the bird it resembles, but it might also be interpreted as a sign of a bird facing into the wind because its streamlined shape reduces the resistance from that direction. A rooster is also used as a symbol of early morning because its habitual crowing makes it an index of dawn. A closer inspection of the weather vane could reveal many other signs: a trademark as a symbol of the manufacturer, the composition of the metal as an index of the manufacturing process and even the source of the ore, and the design as an index of the style or the period when it was made. Finally, a weather vane on a steeple, even when made in the 20th century, could be used as a symbol of a rural 19th-century village with its close ties to the natural forces of wind and weather.
A similar analysis of any physical object or activity, whether natural or artificial, would reveal many such interpretations. Even phenomena originating billions of light years away could be interpreted in different ways by different people at different times. A photograph of some distant light might be interpreted as an index of a black hole, even though the photograph was taken before the concept of black hole had been invented. In summary, the categories of signs do not classify the kinds of beings, but the ways in which phenomena caused by beings may be interpreted.
Like Peirce, Whitehead was a scientist, whose publications included groundbreaking research in algebra, geometry, theoretical physics, and logic. Also like Peirce, he was a voracious reader who studied and debated philosophy with topnotch philosophers throughout his adult life. But as he said in his autobiography, he never stepped inside a philosophy class until he became a professor of philosophy at Harvard at age 63. Whitehead’s major contribution to philosophy is his system of process philosophy or philosophy of organism, which he published in several books that he wrote at Harvard.
In his magnum opus Process and Reality, Whitehead agreed with Heraclitus that “the flux of things is one ultimate generalization around which we must weave our philosophical system.” But he considered the other ultimate generalization to be the “permanences amid the inescapable flux,” which Plato tried to capture in his eternal, unchanging Platonic forms:
Plato found his permanences in a static, spiritual heaven, and his flux in the entanglements of his forms amid the fluent imperfections of the physical world.... Aristotle corrected his Platonism into a somewhat different balance. He was the apostle of “substance and attribute,” and of the classificatory logic which this notion suggests. But on the other side, he makes a masterly analysis of “generation.” Aristotle in his own person expressed a useful protest against the Platonic tendency to separate a static spiritual world from a fluent world of superficial experience.Whitehead’s most significant achievement was the synthesis of Plato and Aristotle with the recent developments in relativity and quantum mechanics. His starting point was Plato’s theory of forms, but with Aristotle’s “correction” that the forms inhere in the physical entities. Then he updated the ancient conceptions of form and matter with the latest developments in physics and mathematics:
Among the many philosophers who have noted strong similarities between the philosophies of Peirce and Whitehead, the first were Charles Hartshorne and Paul Weiss, two of Whitehead’s former students, who edited the first six volumes of Peirce’s Collected Papers. Another was William Reese (1952), who wrote
In general, the logic of Peirce’s thought modifies Whiteheadian cosmology by clearly identifying the basic philosophic categories with modes of being... The result of this mutual play of principle upon concept between the two systems is, we suspect, a position of philosophic realism combining the emphases of both...In fact, the first six of Whitehead’s “categories of existence” can be interpreted as two Peircean triads, as in Figure 3. The physical triad on the left subdivides the category of physical entities, which would correspond to Kant’s category of Actuality. The abstract triad on the right subdivides the category of abstract entities, which would correspond to Kant’s category of Possibility. Kant’s category of Necessity could be added as a third branch to represent the laws, which Peirce subdivided into the laws of logical necessity, physical necessity, and intentional or subjective necessity.
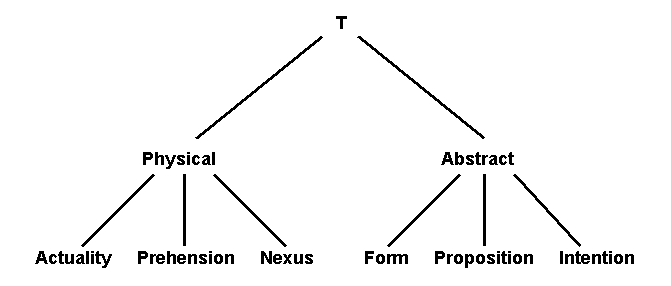
Figure 3: Whitehead’s categories organized in Peircean triads
The physical categories on the left of Figure 3 represent what Whitehead (1929) called “the ultimate facts of immediate actual experience.” The three categories Whitehead defined for actual entities, prehensions, and nexûs make up a triad of physical categories characterized by the Kantian triad under Relation: Inherence, Causality, and Community.
Besides the three physical categories, Whitehead maintained “All else is, for our experience, derivative abstraction.” He classified the abstractions in the categories of eternal objects, propositions, and subjective forms, which constitute a triad of abstract potentials for characterizing inherence, causality, and community (with the proviso that causality is interpreted a broad sense that is close to Aristotle’s aitia).
Although Whitehead understood the power of logic and the value of a good theory, he and Peirce would agree with Leibniz that only an infinite mind, such as God’s, could use logic to deduce all the implications of any initial state of the physical world. Even with the fastest computers, humans would be limited by the principle that Peirce called finite fallibilism. In his last book, Modes of Thought, Whitehead (1938) expressed similar concerns:
Like Peirce and Whitehead, Wittgenstein was a system builder. Unlike Peirce and Whitehead, whose systems reached fruition in their later years, Wittgenstein presented his system in his first book and spent the remainder of his life pointing out the errors in it. For that reason, Wittgenstein is often called antitheoretical because he devoted so much effort to exploding his own and other people’s theories. Yet his method of criticizing theories is theoretical, but it is a metalevel theory about the limitations of any particular object-level theory. In the preface to the Philosophical Investigations, which was published just after his death, Wittgenstein wrote “I should have liked to produce a good book. This has not come about, but the time is past, in which I could improve it.” Although Wittgenstein despaired of ever presenting his later ideas in the elegant form of his first book, he still had a yearning for a grand synthesis, which he realized he could not achieve himself.
Wittgenstein made another intriguing remark in that preface: “I have been forced to recognize grave mistakes in what I wrote in that first book. I was helped to realize these mistakes — to a degree which I am hardly able to estimate — by the criticism which my ideas encountered from Frank Ramsey, with whom I discussed them in innumerable conversations during the last two years of his life.” Many philosophers, starting with Richard Rorty (1961), had noticed similarities between Peirce’s version of pragmatism and Wittgenstein’s later philosophy. After reviewing Ramsey’s published citations of Peirce, Jaime Nubiola (1996) concluded that Ramsey was certainly influenced by Peirce and he probably passed along some Peircean ideas, such as the notion of meaning as use. After those discussions, Wittgenstein dropped the assumption of context-independent meanings and treated language as a game, in which the meaning of a word is determined by its use. That view is consistent with Peirce’s maxim of pragmatism:
Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object. (CP 5.438)
Grammarians have traditionally distinguished three uses for sentences: assertions expressed in the indicative mood, questions in the interrogative mood, and commands in the imperative mood. But as Peirce and Wittgenstein observed, every imaginable purpose can lead to a different kind of use. Wittgenstein (1953) said
There are countless — countless different kinds of use of what we call ‘symbols,’ ‘words,’ ‘sentences.’ And this multiplicity is not something fixed, given once and for all; but new types of language, new language games, as we may say, come into existence, and others become obsolete and get forgotten.As examples of the multiple uses, he cited
Giving orders, and obeying them; describing the appearance of an object, or giving its measurements; constructing an object from a description (a drawing); reporting an event; speculating about an event; forming and testing a hypothesis; presenting the results of an experiment in tables and diagrams; making up a story, and reading it; play acting; singing catches; guessing riddles; making a joke, telling it; solving a problem in practical arithmetic; translating from one language into another; asking, thanking, cursing, greeting, praying.
Inspired by Wittgenstein’s list of uses, Austin (1962) developed his theory of speech acts, each of which represents a different way of using a sentence in natural language. Peirce had made a similar observation: every sentence in a natural language expresses a proposition and its intended use:
A proposition, as I have just intimated, is not to be understood as the lingual expression of a judgment. It is, on the contrary, that sign of which the judgment is one replica and the lingual expression another. But a judgment is distinctly more than the mere mental replica of a proposition. It not merely expresses the proposition, but it goes further and accepts it.... One and the same proposition may be affirmed, denied, judged, doubted, inwardly inquired into, put as a question, wished, asked for, effectively commanded, taught, or merely expressed, and does not thereby become a different proposition. (EP 2.311-312)
Speech acts, as described by Austin, are an important aspect of natural language, but the different ways of using a sentence do not, by themselves, change the meanings of the words that occur in it. Both Peirce and Wittgenstein, however, observed that every symbol, not just the sentences, may have multiple uses. In addition to Austin’s multiple uses for sentences, Wittgenstein’s language games accommodate multiple uses for individual word types. As Peirce said, the “conception” that constitutes the meaning of a word is the totality of the “effects that might conceivably have practical bearings.” When a word is used in a new way, it has new effects, and its corresponding conception is modified by the “practical bearings” of those new effects.
Wittgenstein compared grammar, which determines how words are used in a sentence, to the rules that determine how the pieces are used in a game of chess. The games of go and go-moku illustrated in Figure 1 are even better examples. Each game uses the same stones, the same board, and the same method of two players alternately placing stones on vacant points of the board. The only difference between the two games is in the scoring procedures. As Figure 1 shows, that difference leads to totally different patterns during the course of the games. At a syntactic level, the rules for placing stones are the same, but the meaning of the patterns of stones is determined by the scoring procedures, which are only applied at the end of a game. Besides go and go-moku, other games may be invented that use the same pieces and moves. In another kind of game, the player with the black stones might try to form a continuous path that connects the left and right sides of the board, while the player with white would try to connect the top and bottom. With the same stones and the same syntax, each change in the scoring rules changes the meaning of the patterns.
The practice of reusing old pieces and moves in new games corresponds to metaphors, which are language games that adapt familiar words and syntactic patterns to new subjects and ways of thinking. As an example, consider the metaphorical uses of the verb support in the following sentences:
Tom supported the tomato plant with a stick. Tom supported his daughter with $10,000 per year. Tom supported his father with a decisive argument. Tom supported his partner with a bid of 3 spades.The first sentence uses the verb support in its original sense of physically holding something up. The other sentences are metaphorical extensions that use the same verb and the same syntactic pattern to link the noun phrases in a more abstract domain of discourse:
A person supported NP1 with NP2.Each use of the verb can only be understood with respect to a particular subject matter: physical structures, financial arrangements, intellectual debate, or the game of bridge. Just as the meaning of the pieces and moves in a game will change with differences in the method of computing the score, the meaning of the words in a sentence will change with differences in the subject matter. Metaphor is not a decorative element for expressing emotion in poetry, but an essential mechanism for extending a finite vocabulary to accommodate an open-ended range of subject matter.
As an example of the way meanings evolve, consider the English word car, which was originally an abbreviation of carriage and which came to mean “horseless carriage.” But during the past century, that same word has come to represent computerized metal boxes that would be unrecognizable to the people who coined the term. Those changes were not caused by any linguistic events, but by changes in the subject matter. Over longer periods, even more drastic changes can occur. Figure 4 shows a hierarchy of concept types that includes the English Car and the Chinese Che, which is represented by the character at the top of the hierarchy. The English concept types Car, Taxi, Bus, Truck=Lorry, and Bicycle are subtypes of Vehicle. The Chinese types do not exactly match the English: Che is a supertype of Vehicle that includes Train, which is not usually considered a vehicle in English. The type QiChe (Energy-Che) has no English equivalent, and it includes Car, which has no Chinese equivalent.

Figure 4: Hierarchy with the English Vehicle and the Chinese Che
The original meaning of the word che is illustrated by the icon used to represent it: a simple wagon consisting of a box, one axle (represented by the vertical line through the center), and two wheels (represented by the horizontal lines at top and bottom). That word has evolved to become the generic term, which can be qualified to represent any of the others: a train is a huo-che (fire-che), a bicycle is a zi-xing-che (self-powered-che), a taxi is a chu-zu-qi-che (for-hire-energy-che), and a bus is a gong-gong-qi-che (public-use-energy-che). Although specialized terms have been coined for various subtypes, the word che, by itself, can be used to represent any of them when the context is sufficient to distinguish the details. A Chinese speaker would normally say “Call me a che”, “I’m waiting for the che”, or “I parked my che around the corner.” The listener would either infer the implied subtype from the context or ask a question to resolve the ambiguity.
Wittgenstein’s theory of language games has major implications for both computational linguistics and semantic theory. It implies that the ambiguities of natural language are not the result of careless speech by uneducated people. Instead, they result from the fundamental nature of language and the way it relates to the world: each natural language has a finite number of words that are used and reused to represent an unlimited number of topics. A closed semantic basis along classical lines is not possible for any natural language. Instead of assigning a single meaning or even a fixed set of meanings to each word, a theory of semantics must permit an open-ended number of meanings:
Once a lexical pattern is established for a concrete domain, it can be transferred by metaphor to create similar patterns in more abstract domains. By this process, an initial set of lexical patterns can be built up; later, they can be generalized and extended to form new conceptual patterns for more abstract subjects. The possibility of transferring patterns from one domain to another increases flexibility, but it leads to an inevitable increase in ambiguity.
If the world were simpler, less varied, and less changeable, natural languages might be unambiguous. But the complexity of the world causes the meanings of words to shift subtly from one domain to the next. If a word is used in widely different domains, its multiple meanings may have little or nothing in common. As an example, the word invest, which originally meant to put on clothing, has come to mean either to surround a fortress or to make a certain kind of financial transaction. In Italian, the related word investmento has all the senses of the English investment, but with the added sense of traffic accident. As these examples illustrate, the mechanisms of natural languages not only permit, but actually facilitate shifts in meaning that can be arbitrarily large. They have enabled isolated tribes using stone-age implements to adapt to 21st-century cultures within the lifetime of a single generation, while continuing to speak what is called “the same language.”
According to Peirce and Whitehead, the new foundations for ontology are the same as the old foundations: the philosophia perennis as outlined by Plato and Aristotle, but updated with the more recent developments in science, mathematics, and logic. Whitehead said that all of western philosophy for the past 2,500 years has been a series of footnotes to Plato and Aristotle. Peirce made a similar point, but he expressed it in terms of his trichotomy: there are seven fundamentally different metaphysical systems, each characterized by the combination of Firstness, Secondness, and Thirdness that it recognizes (EP 2.179-195):
An ontology that synthesizes the insights of Peirce, Whitehead, and Wittgenstein would belong to the seventh system of metaphysics. It would therefore include Peirce’s trichotomy and its use as a metalevel principle for generating all the triads needed for a complete theory of semiotics. It would also include Whitehead’s process philosophy, but with the categories reorganized in Peircean triads. Although Wittgenstein never formalized his theory of language games, each language game could be identified with a kind of microtheory as used in many AI systems. Winograd’s SHRDLU system implemented a simple, but rather limited example of a microtheory for a world consisting of blocks moved by a robot. R. V. Guha (1991) introduced collections of microtheories into the vastly more complex Cyc system in order to make it more modular and more adaptable to a wide range of applications.
Multiple Hierarchies. As a way of formalizing a structure of microtheories to accommodate an open-ended, possibly inconsistent knowledge soup, Sowa (1990c, 2000) proposed to organize them in an infinite lattice, which would be rich enough to include any possible language game that any finite reasoner (human, computer, or extraterrestrial) could ever invent. Central to the framework is a partitioning of the knowledge base into four separate hierarchies with appropriate mappings to link them. A multilingual system of N languages would have 2N+2 hierarchies.
Theories, Models, and the World. The problems of knowledge soup result from the difficulty of matching theories based on discrete concepts to the continuum of physical world. The AI techniques of fuzziness, probability, defaults, revisions, and relevance are different ways of measuring, evaluating, or accommodating the inevitable mismatch. Each technique is a metalevel approach to the task of finding or constructing a theory and determining how well it approximates reality. To bridge the gap between theories and the world, Figure 5 shows models as Janus-like structures, with an engineering side facing the world and an abstract side facing the theories.

Figure 5: Relating a theory to the world
On the left is a picture of the physical world, which contains more detail and complexity than any humanly conceivable model or theory can represent. In the middle is a mathematical model that represents a domain of individuals D and a set of relations R over D. If the world had a unique decomposition into discrete objects and relations, the world itself would be a universal model, of which all accurate models would be subsets. But as the examples of knowledge soup have shown (Sowa 1990c, 2000), the selection of a domain and its decomposition into objects depends on the intentions of some agent and the limitations of the agent’s measuring instruments. Even the best models are approximations to a limited aspect of the world for a specific purpose. The statistician George Box expressed that point in a pithy slogan: All models are wrong, but some are useful.
The two-stage mapping from theories to models to the world replaces the direct mapping of sentences to the world as characterized by two diametrically opposed views of semantics: the Ockham-Tarski version of model theory, and the version of fuzzy logic by Lotfi Zadeh (1975). In the Ockham-Tarski approach, each sentence has two possible truth values: {true, false}. In fuzzy logic, a sentence may have a continuous range of possible values from 0.0 for certainly false to 1.0 for certainly true; intermediate values would represent hedging terms, such as likely, unlikely, very nearly true, or almost certainly false. Susan Haack (1978, 1996) was one of the early critics of fuzzy logic, and she has continued to sharpen her arguments against the claims that natural language justifies or even requires “degrees of truth.” Her most serious criticism is not that fuzzy logic is vague, but that it is too precise: instead of modeling the way people talk and think about vagueness, fuzzy logic forces an unwarranted quantification of vagueness. The two-stage mapping of Figure 5, however, makes room for both kinds of reasoning: a rigorous two-valued logic for evaluating the truth of a mathematical theory in terms of a model; and a continuum of fuzzy values that measure the suitability of a particular model for a particular purpose in actions upon the world. Such two-stage mappings have long been used in science and engineering: a strict two-valued logic is necessary for mathematical reasoning, and a continuum of values is used for quantifying experimental error and degree of approximation.
Searching the Lattice of Theories. Although the world is bigger than any human can comprehend or any computer can compute, the sets of all possible theories and models are even bigger. The entire universe contains a finite number of atoms, but the lattice of all possible theories is infinite, and the set of models of those theories is uncountably infinite. The ultimate task of science is to search that vast infinity in the hope of finding a theory that gives the best answers to all possible questions. Yet that search may be in vain. Perhaps no single theory is best for all questions; even if one theory happened to be the best, there is no assurance that it would ever be found; and even if somebody found it, there might be no way to prove that it is the best.
Engineers have a more modest goal. Instead of searching for the best possible theory for all problems, they are satisfied with a theory that is good enough for the specific problem at hand. When they are assigned a new problem, they look for a new theory that can solve it to an acceptable approximation within the constraints of available tools, budgets, and deadlines. Although no one has ever found a theory that can solve all problems, people everywhere, from prehistoric times to the present, have been successful in finding more or less adequate theories that can deal with the routine problems of daily life. As science progresses, engineering techniques advance with it, but the engineers do not have to wait for a perfect theory before they can do their work.
From each theory, the partial ordering of the lattice determines the paths to more general theories above and more specialized theories below. Figure 6 shows four basic ways of moving along the paths from one theory to another: contraction, expansion, revision, and analogy. Each move corresponds to one of the four operators for belief revision or theory revision. The first three operators are defined by the AGM axioms (Alchourrón et al. 1985); the fourth operator, which revises a theory by renaming the labels of types and relations, is defined by Sowa (2000).
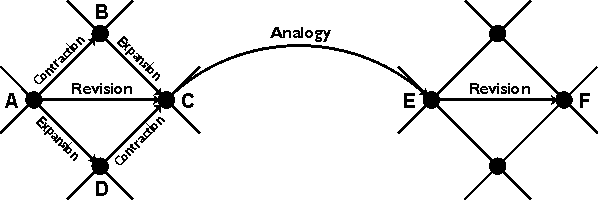
Figure 6: Four belief-revision operators
To illustrate the moves through the lattice, suppose that theory A is Newton’s theory of gravitation applied to the earth revolving around the sun and that F is Niels Bohr’s theory about an electron revolving around the nucleus of a hydrogen atom. The path from A to F is a step-by-step transformation of the old theory to the new one. The revision step from A to C replaces the gravitational attraction between the earth and the sun with the electrical attraction between the electron and the proton. That step can be carried out in two intermediate steps:
By repeated application of the four operators in Figure 6,
any theory or collection of beliefs can be converted into any other.
Multiple contractions would reduce a theory to the empty
or universal theory  at the top of the lattice
that contains only the tautologies that are true of everything.
Multiple expansions would lead to the inconsistent or
absurd theory
at the top of the lattice
that contains only the tautologies that are true of everything.
Multiple expansions would lead to the inconsistent or
absurd theory 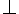 at the
bottom of the lattice, which contains all axioms and is true of nothing.
The analogy operator allows short cuts that can jump across the lattice
by a systematic relabeling of the types and relations.
If the original theory is consistent, the analogy must also be consistent,
since the axioms are identical except for a change of names.
at the
bottom of the lattice, which contains all axioms and is true of nothing.
The analogy operator allows short cuts that can jump across the lattice
by a systematic relabeling of the types and relations.
If the original theory is consistent, the analogy must also be consistent,
since the axioms are identical except for a change of names.
Each step through the lattice of theories is simple in itself, but the infinity of possible steps makes it difficult for both people and computers to find the best theory for a particular problem. Newton became famous for finding the axioms that explain the solar system, and Bohr won the Nobel Prize for revising them to explain the atom.
Abduction. Of the three reasoning methods in Peirce’s methodeutic, abduction is the only one that can introduce a truly novel idea. It is the method that generates Einstein’s “free creations of thought which cannot be inductively derived from sense experiences.” In Peirce’s system, abduction is the replacement for Descartes’s innate ideas and for Kant’s synthetic a priori judgments. Abduction may be considered a process of selecting chunks from the knowledge soup, evaluating their relevance to the problem at hand, and assembling them into a novel combination. Abduction may be performed at various levels of complexity:
The elements of every concept enter into logical thought at the gate of perception and make their exit at the gate of purposive action; and whatever cannot show its passports at both those two gates is to be arrested as unauthorized by reason. (EP 2.241).Note Peirce’s word elements: abduction does not create totally new elements, but it can reassemble previously observed elements in novel combinations. Each combination defines a new concept, whose full meaning is determined by the totality of purposive actions it implies. As Peirce said, meanings grow as new information is received, new implications are derived, and new actions become possible.
Logic of Pragmatism. In its narrow sense, abduction is one of three methods of reasoning in Peirce’s methodeutic. In its broader sense, which includes induction for discovering the elements and deduction for deriving the implications, Peirce identified abduction with the logic of pragmatism. To illustrate the relationships, Figure 7 shows an agent who repeatedly carries out the stages of induction, abduction, deduction, and action. The arrow of induction indicates the accumulation of patterns that have been useful in previous applications. The crystal at the top symbolizes the elegant, but fragile theories that are constructed from chunks in the knowledge soup by abduction. The arrow above the crystal indicates the process of belief revision, which uses repeated abductions to modify the theories by expansion, contraction, revision, and analogy. At the right is a prediction derived from a theory by deduction. That prediction leads to actions whose observable effects may confirm or refute the theory. Those observations are the basis for new inductions, and the cycle continues.

Figure 7: Peirce’s logic of pragmatism
As Figure 7 illustrates, the chunks of knowledge in the soup enter through the gate of perception and are recognized as repeatable patterns by the process of induction. The crystalline theories at the top are hypotheses assembled by abduction. Those theories whose predictions lead to successful actions are added to the soup as chunks that become available for further abductions. The more often a chunk is used, the higher its salience or likelihood for future selections.
Learning is the process of accumulating chunks of knowledge in the soup and organizing them into theories — collections of consistent beliefs that prove their value by making predictions that lead to successful actions. Learning by any agent — human, animal, or robot — involves a constant cycling from data to models to theories and back to a reinterpretation of the old data in terms of new models and theories. Beneath it all, there is a real world, which the entire community of inquirers learns to approximate through repeated cycles of induction, abduction, deduction, and action.
Truth as the Aim of Inquiry. To evaluate the truth of his axioms and rules of inference, Peirce (1909) had developed a version of model-theoretic semantics, but he was dissatisfied with a definition of truth as a static correspondence between a sentence and a particular model of the world. Instead, he believed in a potential infinity of mathematical models, which could be applied to various aspects of the world, but he also rejected a relativistic view that all models are equally good. Instead, he defined truth as the ultimate goal of a search through an infinity of models that give better and better approximations to a wider range of phenomena. The denotation of a proposition in terms of a particular model must be supplemented with the scientific methods of experiment, observation, and test to determine whether the model is an adequate approximation to the world for the purpose at hand. Following are some quotations in which Peirce summarized that view:
Peirce’s definition of truth and his logic of pragmatism, which supports that definition, are an elegant generalization of the practices of working scientists. Yet many philosophers who seized upon one brief quotation have failed to appreciate their full ramifications. In a survey of various theories of truth, Kirkham (1992) said
Peirce’s theory of truth is plausible only because it is parasitic on another, hidden theory of truth: truth as correspondence with reality. So why doesn’t Peirce simply offer the latter as his theory of truth? (p. 83)If he had read more of Peirce’s writings, Kirkham might have found the answer to his question:
That truth is the correspondence of a representation with its object is, as Kant says [1787, A58, B82], merely the nominal definition of it. Truth belongs exclusively to propositions. A proposition has a subject (or set of subjects) and a predicate. The subject is a sign; the predicate is a sign; and the proposition is a sign that the predicate is a sign of that of which the subject is a sign. If it be so, it is true. But what does this correspondence, or reference of the sign to its object, consist in? The pragmaticist answers this question as follows... if we can find out the right method of thinking and can follow it out, — the right method of transforming signs, — then truth can be nothing more nor less than the last result to which the following out of this method would ultimately carry us. (EP 2.379-380)
Quine (1960) is more subtle, but he hadn’t read much more of Peirce’s writings than Kirkham:
But there is a lot wrong with Peirce’s notion, besides its assumption of a final organon of scientific method and its appeal to an infinite process. There is a faulty use of numerical analogy in speaking of a limit of theories, since the notion of limit depends on that of “nearer than,” which is defined for numbers and not for theories. And even if we by-pass such troubles by identifying truth somewhat fancifully with the ideal result of applying scientific method outright to the whole future totality of surface irritations, still there is trouble in the imputation of uniqueness (“the ideal result“).... It seems likelier, if only on account of symmetries or dualities, that countless alternative theories would be tied for first place. (p. 23)
Quine’s objection has three parts, each of which requires a separate answer:
Conclusion. To deal with meaning, semiotics must go beyond relationships between signs to the relationships of signs, the world, and the agents who observe the world, interpret it in signs, and use the signs to plan further actions upon the world. Peirce’s recognition of the ubiquity of signs enabled him to bridge the mind-body dichotomy: the mind itself is a sign formed by a complex structure of other signs, which are related by the methods of perception and action to the world and to all the people who communicate with each other in languages that express the multitudes of signs in their minds. Every living being, down to the level of single-celled bacteria, is a semiotic processor that responds to signs by generating more signs. The human brain is the most advanced of all known semiotic processors, but the signs it processes are simple compared to the signs encoded in DNA that generate every living thing including the human brain itself. This view by Peirce is compatible with the complementary positions by Whitehead and Wittgenstein. Together, the three of them provide the necessary counterbalance to the extreme nominalism of 20th-century analytic philosophy.
Note. Except for some minor editing, this article is unchanged from the version in 2001. For more recent articles on related issues see the citations below to Sowa (2005, 2006, 2007, 2010, 2013).
Almog, Joseph, John Perry, & Howard Wettstein (1989) Themes from Kaplan, Oxford University Press, Oxford.
Annas, Julia, & Jonathan Barnes (1985) The Modes of Scepticism: Ancient Texts and Modern Interpretations, Cambridge University Press, Cambridge.
Austin, John L. (1962), How to do Things with Words, second edition edited by J. O. Urmson & Marina Sbisá, Harvard University Press, Cambrige, MA, 1975.
Bailey, David, (1997) A Computational Model of Embodiment in the Acquisition of Action Verbs, Doctoral dissertation, Computer Science Division, EECS Department, University of California, Berkeley.
Barwise, Jon, & John Perry (1983) Situations and Attitudes, MIT Press, Cambridge, MA.
Bratman, Michael E. (1987) Intentions, Plans, and Practical Reason, Harvard University Press, Cambridge, MA.
Carnap, Rudolf (1928) Der logische Aufbau der Welt, English translation The Logical Structure of the World, University of California Press, Berkeley, 1967.
Carnap, Rudolf (1934) Logische Syntax der Sprache, translated as The Logical Syntax of Language, Humanities Press, New York, 1937.
Carnap, Rudolf (1947) Meaning and Necessity, University of Chicago Press, Chicago. Second edition 1956.
Carnap, Rudolf (1954) Einführung in die symbolische Logik, translated by W. H. Meyer & J. Wilkinson as Introduction to Symbolic Logic and its Applications, Dover Publications, New York.
Carnap, Rudolf, Otto Neurath, & Hans Hahn (1929) Wissenschaftliche Weltauffassung der Wiener Kreis, A. Wolf, Vienna.
Church, Alonzo (1958) The ontological status of women and abstract entities, Lecture presented at Harvard University on April 18, 1958, available at http://www.jfsowa.com/ontology/church.htm
Comte, Auguste (1830-1842) Cours de Philosophie positive, selections translated by Margaret Clarke as The Essential Comte, Barnes & Noble, New York, 1974.
Davidson, Donald (1967) The logical form of action sentences, reprinted in D. Davidson (1980) Essays on Actions and Events, Clarendon Press, Oxford, pp. 105-148.
Donnellan, Keith S. (1966) Reference and definite descriptions, Philosophical Review 75:3, 281-304.
Einstein, Albert (1944) Remarks on Bertrand Russell’s Theory of Knowledge, in P. A. Schilpp, ed., The Philosophy of Bertrand Russell, Library of Living Philosophers.
Fellbaum, Christiane, ed. (1998) WordNet: An Electronic Lexical Database, MIT Press, Cambridge, MA.
Förster, Eckart (2000) Kant’s Final Synthesis: An Essay on the Opus postumum, Harvard University Press, Cambridge, MA.
Frege, Gottlob (1879) Begriffsschrift, English translation in J. van Heijenoort, ed. (1967) From Frege to Gödel, Harvard University Press, Cambridge, MA, pp. 1-82.
Goodman, Nelson (1951) The Structure of Appearance, Bobbs-Merrill Co., New York. Second edition 1966.
Guha, R. V. (1991) Contexts: A Formalization and Some Applications, PhD dissertation, Stanford, and Technical Report ACT-CYC-423-91, MCC, Austin, TX.
Haack, Susan (1978) Philosophy of Logics, Cambridge University Press, Cambridge.
Haack, Susan (1996) Deviant Logic, Fuzzy Logic, University of Chicago Press, Chicago.
Hilpinen, Risto (1982) On C. S. Peirce’s theory of the proposition: Peirce as a precursor of game-theoretical semantics, The Monist 65, 182-88.
Kant, Immanuel (1787) Kritik der reinen Vernunft, translated by N. Kemp Smith as Critique of Pure Reason, St. Martin’s Press, New York.
Kaplan, David (1989) Afterthoughts, in Almog et al. (1989) pp. 565-614.
Kaye, Sharon (1998) Russell, Strawson, and William of Ockham, Twentieth World Congress of Philosophy, Boston.
Kirkham, Richard L. (1992) Theories of Truth: A Critical Introduction, MIT Press, Cambridge, MA.
Kripke, Saul A. (1977) Speaker’s reference and semantic reference, in P. A. French, T. F. Uehling, & H. K. Wettstein, eds., Contemporary Perspecives in the Philosophy of Language, University of Minnesota Press, Minneapolis, pp. 6-27.
Kuntz, Paul Grimley (1984) Alfred North Whitehead, Twayne Publishers, Boston.
Lakoff, George, & Mark Johnson (1999) Philosophy in the Flesh: The Embodied Mind and its Challenge to Western Thought, Basic Books, New York.
Lenat, Douglas B. (1995) A large-scale investment in knowledge infrastructure, Communications of the ACM 38:11, 33-38.
Lenat, D. B., & R. V. Guha (1990) Building Large Knowledge-Based Systems, Addison-Wesley, Reading, MA.
Lindley, David (2001) Boltzmann’s Atom: The Great Debate that Launched a Revolution in Physics, Free Press, New York.
Lucas, George R., Jr. (1989) The Rehabilitation of Whitehead, State University of New York Press, Albany.
Mach, Ernst (1886) Beiträge zur Analyse der Empfindungen, translated as The Analysis of Sensations by C. M. Williams and Sydney Waterlow, Dover, New York.
Mann, Wolfgang-Rainer (2000) The Discovery of Things: Aristotle’s Categories and their Context, Princeton University Press, Princeton.
Miller, George A. (1995) WordNet: A lexical database for English, Communications of the ACM 38:11, 39-41.
Montague, Richard (1970) English as a formal language, reprinted in R. Montague, Formal Philosophy, Yale University Press, New Haven, pp. 188-221.
Morris, Charles W. (1946) Signs, Language, and Behavior, Prentice-Hall, New York.
Narayanan, Srini (1997) Embodiment in Language Understanding: Sensory-Motor Representations for Metaphoric Reasoning About Event Descriptions, Doctoral dissertation, Computer Science Division, EECS Department, University of California, Berkeley.
Nubiola, Jaime (1996) Scholarship on the relations between Ludwig Wittgenstein and Charles S. Peirce, in I. Angelelli & M. Cerezo, eds., Proceedings of the III Symposium on the History of Logic, Gruyter, Berlin.
Ockham, William of (1323) Summa Logicae, Part II translated as Ockham’s Theory of Propositions by A. J. Freddoso and H. Schuurman, University of Notre Dame Press, Notre Dame, IN, 1980. The edition owned by C. S. Peirce was published by Johannes Higman, Paris, 1488.
O’Keefe, J., & L. Nadel (1979) The hippocampus as a cognitive map, Behavioral and Brain Sciences 2:4.
Peirce, Charles Sanders (1891) Review of Principles of Psychology by William James, Nation, vol. 53, p. 32.
Peirce, Charles Sanders (1898) Reasoning and the Logic of Things, The Cambridge Conferences Lectures of 1898, ed. by K. L. Ketner, Harvard University Press, Cambridge, MA, 1992.
Peirce, Charles Sanders (1909) Manuscript 514, with commentary by J. F. Sowa, available at http://www.jfsowa.com/pubs/egtut.pdf
Peirce, Charles Sanders (CP) Collected Papers of C. S. Peirce, ed. by C. Hartshorne, P. Weiss, & A. Burks, 8 vols., Harvard University Press, Cambridge, MA, 1931-1958.
Peirce, Charles Sanders (EP) The Essential Peirce, ed. by N. Houser, C. Kloesel, and members of the Peirce Edition Project, 2 vols., Indiana University Press, Bloomington, 1991-1998.
Perlis, Alan J. (1982) Epigrams in Programming, SIGPLAN Notices, Sept. 1982, ACM.
Perry, John (1979) The problem of the essential indexical, Nous, vol. 13, pp. 3-21.
Quine, Willard Van Orman (1960) Word and Object, MIT Press, Cambridge, MA.
Reese, William (1952) Philosophic Realism: A Study in the Modality of Being in Peirce and Whitehead, in Philip P. Wiener & Frederic H. Young, eds., Studies in the Philosophy of Charles Sanders Peirce, Harvard University Press, pp. 225-237.
Regier, Terry (1996) The Human Semantic Potential: Spatial Language and Constrained Connectionism, MIT Press, Cambridge,
Rescher, Nicholas (1962) The revolt against process, Journal of Philosophy, vol. 59, pp. 410-417. Revised version reprinted in Rescher, Essays in Philosophical Analysis, University of Pittsburgh Press, pp. 181-190.
Rorty, Richard (1961) Pragmatism, Categories, and Language, Philosophical Review 70, 197-223.
Russell, Bertrand (1905) On denoting, Mind 14.
Russell, Bertrand (1918) The Philosophy of Logical Atomism, The Monist, reprinted in Russell (LA) pp. 35-155.
Russell, Bertrand (1924) Logical Atomism, in J. H. Muirhead, ed., Contemporary British Philosophy, London, reprinted in Russell (LA) pp. 157-181.
Russell, Bertrand (1969) Mr. Strawson on referring, in My Philosophical Development, Unwin Hyman Limited, London, pp. 238-245.
Russell, Bertrand (LA) The Philosophy of Logical Atomism, Open Court, La Salle, IL, 1985.
Searle, John R. (1969), Speech Acts. An Essay in the Philosophy of Language, Cambridge University Press, Cambridge.
Searle, John R. (1982), Intentionality. An Essay in the Philosophy of Mind, Cambridge University Press, Cambridge.
Searle, John R. (1995), The Construction of Social Reality, Free Press, New York.
Smith, Barry (1995) Formal ontology, common sense, and cognitive science, International J. of Human-Computer Studies 43, 641-668.
Smith, Barry (1998) Basic Concepts of Formal Ontology, in Guarino (1995) pp. 19-28.
Smith, Barry (1999) Les objets sociaux, Pilosophiques 26:2, 315-347. English version at http://wings.buffalo.edu/philosophy/ontology/socobj.htm
Smith, Barry, & John Searle (2001) The construction of social reality: an exchange, American Journal of Economics and Sociology 60, available at http://wings.buffalo.edu/philosophy/faculty/smith/articles/dksearle.htm
Sowa, John F. (1990) Crystallizing theories out of knowledge soup, in Z. W. Ras & M. Zemankova, eds., Intelligent Systems: State of the Art and Future Directions, Ellis Horwood Ltd., London, 1990, pp. 456-487.
Sowa, John F. (2000) Knowledge Representation: Logical, Philosophical, and Computational Foundations, Brooks/Cole Publishing Co., Pacific Grove, CA.
Sowa, John F. (2005) The Challenge of Knowledge Soup, in J. Ramadas & S. Chunawala, Research Trends in Science, Technology and Mathematics Education, Homi Bhabha Centre, Mumbai, 55-90. http://www.jfsowa.com/pubs/challenge.pdf
Sowa, John F. (2006) Peirce’s contributions to the 21st Century, in H. Schärfe, P. Hitzler, & P. ěhrstr°m, eds., Conceptual Structures: Inspiration and Application, LNAI 4068, Springer, pp. 54-69. http://www.jfsowa.com/pubs/csp21st.pdf
Sowa, John F. (2007) Language Games, A Foundation for Semantics and Ontology, in A-V Pietarinen, ed., Game Theory and Linguistic Meaning, Elsevier, pp. 17-37. http://www.jfsowa.com/pubs/lgsema.pdf
Sowa, John F. (2009) Responses to five questions on signs and meaning, in Signs and Meaning: 5 Questions, edited by Peer Bundgaard and Frederik Stjernfelt, Automatic Press, New York. http://www.jfsowa.com/pubs/5qsigns.htm
Sowa, John F. (2010) The role of logic and ontology in language and reasoning, Chapter 11 of Theory and Applications of Ontology: Philosophical Perspectives, edited by R. Poli & J. Seibt, Berlin: Springer, pp. 231-263. http://www.jfsowa.com/pubs/rolelog.pdf
Sowa, John F. (2013) From existential graphs to conceptual graphs, International Journal of Conceptual Structures 1:1, pp. 39-72. http://www.jfsowa.com/pubs/eg2cg.pdf
Strawson, Peter F. (1950) On referring, Mind 59, 320-344.
Strawson, Peter F. (1959) Individuals: An Essay in Descriptive Metaphysics, Methuen and Co., London.
Strawson, Peter F. (1992) Analysis and Metaphysics: An Introduction to Philosophy, Oxford University Press, Oxford.
Talmy, Leonard (1983) How languages structure space, in H. L. Pick & L. P. Acredolo, eds, Spatial Orientation: Theory, Research, and Application, New York, Plenum Press, pp. 225-282.
Tarski, Alfred (1933) Pojęcie prawdy w językach nauk dedukcynych, German version (1936) Der Wahrheitsbegriff in den formalisierten Sprachen, translated as The concept of truth in formalized languages, in Tarski (1982) pp. 152-278.
Tarski, Alfred (1936) Über den Begriff der logischen Folgerung, translated as On the concept of logical consequence in Tarski (1982) pp. 409-420.
Tarski, Alfred (1982) Logic, Semantics, Metamathematics, Second edition, Hackett Publishing Co., Indianapolis.
Tenny, Carol L., & James Pustejovsky, eds. (2000) Events as Grammatical Objects: The Converging Perspectives of Lexical Semantics and Syntax, CSLI Publications, Stanford, CA.
Tolman, Edward C. (1948) Cognitive maps in rats and men, Psychological Review 55:4, 189-208.
Whitehead, Alfred North (1929) Process and Reality: An Essay in Cosmology, corrected edition edited by D. R. Griffin & D. W. Sherburne, Free Press, New York, 1978.
Whitehead, Alfred North (1933) Adventures of Ideas, Macmillan, New York.
Whitehead, Alfred North (1937) Analysis of Meaning, Philosophical Review, reprinted in A. N. Whitehead, Essays in Science and Philosophy, Philosophical Library, New York, pp. 122-131.
Whitehead, Alfred North (1938) Modes of Thought, Macmillan Co., New York.
Wigner, Eugene (1960) The unreasonable effectiveness of mathematics in the natural sciences, Communications in Pure and Applied Mathematics 13:1.
Winograd, Terry (1972) Understanding Natural Language, Academic Press, New York.
Winograd, Terry, & Fernando Flores (1986) Understanding Computers and Cognition, Ablex, Norwood, NJ.
Wittgenstein, Ludwig (1922) Tractatus Logico-Philosophicus, Routledge & Kegan Paul, London.
Wittgenstein, Ludwig (1953) Philosophical Investigations, Basil Blackwell, Oxford.
Yokoi, Toshio (1995) The EDR electronic dictionary, Communications of the ACM 38:11, 42-44.
Zadeh, Lotfi A. (1975) Fuzzy logic and approximate reasoning, Synthese 30, 407-428.
Copyright ©2001, 2015 by John F. Sowa
Last Modified: