Laws, Facts, and Contexts:
Foundations for Multimodal Reasoning
John F. Sowa
Abstract.
Leibniz's intuition that necessity corresponds to truth in all possible
worlds enabled Kripke to define a rigorous model theory for several
axiomatizations of modal logic. Unfortunately, Kripke's model structures
lead to a combinatorial explosion when they are extended to all the
varieties of modality and intentionality that people routinely use
in ordinary language. As an alternative, any semantics based on possible
worlds can be replaced by a simpler and more easily generalizable
approach based on Dunn's semantics of laws and facts and
a theory of contexts based on the ideas of Peirce and McCarthy.
To demonstrate consistency, this paper defines a family of nested
graph models, which can be specialized to a wide variety of model
structures, including Kripke's models, situation semantics, temporal
models, and many variations of them. An important advantage of
nested graph models is the option of partitioning the reasoning tasks
into separate metalevel stages, each of which can be axiomatized
in classical first-order logic. At each stage, all inferences
can be carried out with well-understood theorem provers for FOL
or some subset of FOL. To prove that nothing more than FOL is required,
Section 6 of this paper shows how any nested graph model with a finite
nesting depth can be flattened to a conventional Tarski-style
model. For most purposes, however, the nested models are computationally
more tractable and intuitively more understandable.
This is a talk that was presented at the
Φlog Conference
at the University of Roskilde, Denmark, on 4 May 2002.
Summary
Semantics based on laws, facts, and contexts...
- Includes Kripke's semantics as a special case.
- Avoids a dubious ontology of possible worlds.
- Derives the accessibility relation from more basic
principles instead of assuming it as a primitive.
- Puts the agent at the center of intentional modalities,
such as knowing, believing, hoping, fearing, and desiring.
- Makes it possible to reason about multiple modalities
and multiple interacting agents within a common framework.
Topics Leading to the Summary
- Dunn's semantics based on laws and facts instead of possible worlds.
- Contexts by Peirce and McCarthy.
- Tarski's hierarchy of metalevels.
- Nested graph models (NGMs).
- Flattening the nest.
- Classification of Modalities.
Laws and Facts
- Replacement for (or, if you like, a representation of) possible worlds.
- Each world w is replaced (or represented) by
a set of facts M and a set of laws L,
where L⊂M.
- p is true iff p∈M.
- op iff L |= p.
- ◊p iff not L |= ~p.
Dunn's Innovation
Define accessibility R
from a world w1 to a world w2
to mean that the laws L1 are a subset
of the facts M2:
R(w1,w2) ≡
L1⊂M2.
Implications:
- System S4 implies that the laws of the first
world must be a subset of the laws of the second world.
- System S5 implies that all worlds accessible from a given
world must have the same laws.
Result: All modal and multimodal reasoning can be treated
as metalevel reasoning about the laws and facts.
Contexts
Next step is to define a theory of contexts that clearly
separates the metalevel from the object level.
- Syntax.
The function of grouping, quoting, delimiting,
or packaging a section of text.
- Semantics.
Describing or characterizing
some real or hypothetical situation.
- Pragmatics.
The reason or purpose for quoting some section of linguistic text
or characterizing some nonlinguistic situation.
Peirce's Contexts
Peirce used an oval to group or quote a proposition to be discussed:

Negated Contexts
Since p⊂q is equivalent to
~(p ∧ ~q), Peirce used a nest of two
negations to represent implication:

Kamp's Discourse Representation Structures
For his discourse representation theory,
Hans Kamp independently developed an isomorphic notation
for representing context-dependent indexicals:

Modal Contexts
In 1906, Peirce introduced colors or shading
to represent modal contexts:

"You can lead a horse to water, but you can't make him drink."
Modal Contexts
Corresponding conceptual graph:

"You can lead a horse to water, but you can't make him drink."
Multiple Modalities
English Sentence: "Tom believes that Mary wants to marry a sailor."

Changing Scope
English sentence: "There is a sailor that Tom believes Mary
wants to marry."

McCarthy's Contexts
John McCarthy introduced the predicate isTrueIn(C,p)
to say that p is true in context C:
- isTrueIn(contextOf("Sherlock Holmes stories"),
"Holmes is a detective").
- isTrueIn(contextOf("U.S. legal history"),
"Holmes is a Supreme Court Justice").
To combine Dunn's semantics with McCarthy's contexts,
introduce another predicate isLawOf:
- Facts:
M = {p | isTrueIn(C,p)}.
- Laws:
L = {p | isLawOf(C,p)}.
Truth is now a context-dependent indexical.
Tarski's Metalevels
- The object language L0 refers to entities
in a universe of discourse D.
-
The metalanguage L1 refers to the
symbols of L0 and their relationships
to D.
-
The metalanguage L1
is still first order, but its universe of discourse
is enlarged from D to
L0∪D.
-
The
metametalanguage L2 is also first order, but its universe
of discourse is L1∪L0∪D.
-
To avoid paradoxes, Tarski insisted that no metalanguage
Ln
could refer to its own symbols,
but it could refer to the symbols or the domain of any language
Li
where 0≤i<n.
-
At every level of the Tarski hierarchy of metalanguages, the reasoning
process is governed by first-order rules.
-
But first-order reasoning in language Ln
has the effect of higher-order or modal reasoning for every language
below n.
Example
Illustrate metalevel reasoning on a sample English sentence:
Joe said "I don't believe in astrology, but they say
that it works even if you don't believe in it."
- Mark indexicals with the # symbol, and mark
nested contexts with square brackets:
Joe said
[#I don't believe [in astrology]
but #they say
[[#it works]
even if #you don't believe [in #it]]].
- Resolve indexicals: #I = Joe;
"they say" = "every person believes";
#it = astrology;
#you = "every person".
Joe said
[Joe doesn't believe [astrology works]
but every person x believes
[[astrology works]
even if x doesn't believe
[astrology works] ]].
- If Joe was sincere, he believes what he said, and
a statement of the form "p even if q" implies p.
Joe believes
[Joe doesn't believe [astrology works]
and every person x believes
[astrology works] ].
- Substitute "Joe" for x in
"every person x":
Joe believes
[Joe doesn't believe [astrology works]
and Joe believes [astrology works] ].
- Substitute p for
"Joe believes [astrology works]":
Joe believes [p ∧ ~p].
Nested Graph Models
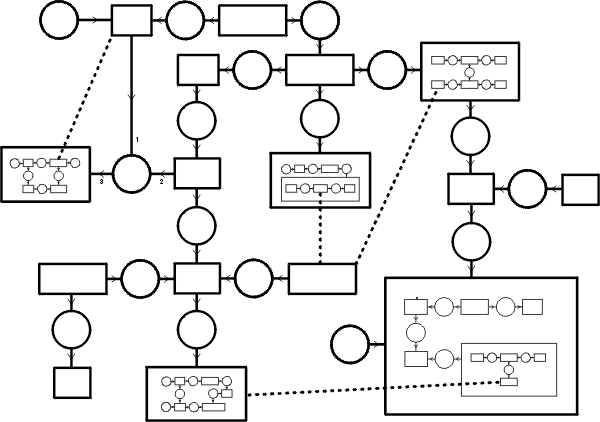
Specializing NGMs
Nested graph models can be specialized for a wide variety of purposes:
- Flat Tarski-style models.
- Kripke-style models.
- Kripke models with counterparts.
- Barcan models.
- Temporal models.
Situations

Mapping possible worlds to situations and contexts
Flattening the Nest
To demonstrate that nothing more than FOL is being used, it is possible
to flatten any NGM to a conventional Tarski-style model:
- Observe that contexts are a syntactic device for partitioning
the name space for individuals and relations.
- It is possible to assign a unique name to every context.
- Then append the name of any context x as an extra
argument to every relation that occurs in x.
- Use restricted quantifiers to limit the range of any
quantifier that occurs in context x to the entities that
appear in x.
- Then erase all the context brackets.
Why Flattening is a Bad Idea
The possibility of flattening an NGM shows that the semantics is first-order.
But the act of flattening is usually unwise:
- Readability is reduced by
extra arguments on quantifiers and relations.
- Erasing context brackets mixes everything in one large pot.
- Removing separations between metalevels allows
paradoxical references.
Actuality, Modality, Intentionality

Peirce's classification of contexts
Actuality vs. Modality
Peirce considered two ways of talking about what is actual:
- What is asserted (affirmo) is written on the front of a sheet.
- What is denied (nego) is written on the back of the sheet
or inside an oval context.
But for modality, Peirce suggested a pad of paper:
- Possibility, Σωp, is "inscribed" on
some sheet(s) to say that it is true in some "state of affairs".
- Necessity, Πωp, is "inscribed" on
every sheet to say that it is true in every "state of affairs".
Modality
Peirce's classification of 1906:
- Logical possibility.
- Σωp means p is consistent or not provably false.
- Πωp means p is provable.
- Subjective possibility.
- Σωp means p is believable or not known to be false.
- Πωp means p is known
or not believably false.
- Objective possibility.
- Σωp means p is physically possible.
- Πωp means p is
necessary according to the laws of physics.
- Interrogative mood.
- Σωp means p is questioned.
- Πωp means p is
unquestionably true.
- Freedom.
- Σωp means p is free or permissible.
- Πωp means p is
required or not freely false.
Intentionality
- Depends on a triadic relation that involves some agent.
- For an intentional context C,
isLawOf(C,p) ≡
(∃a:Agent)legislate(a,p,C).
- Questions to consider:
- How does an agent learn what laws are appropriate for some
context?
- How does an agent learn what some other agent has legislated
for some context?
- How do multiple agents debate, question, communicate,
or negotiate what become the laws of a context?
Summary
Semantics based on laws, facts, and contexts...
- Includes Kripke's semantics as a special case.
- Avoids a dubious ontology of possible worlds.
- Derives the accessibility relation from more basic
principles instead of assuming it as a primitive.
- Puts the agent at the center of intentional modalities,
such as knowing, believing, hoping, fearing, and desiring.
- Makes it possible to reason about multiple modalities
and multiple interacting agents within a common framework.
Copyright ©2002, John F. Sowa










