'\0395\03BB\03BB\03AC\03B4\03B1' denotes the 6-character Unicode sequence 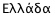 .
.Latest version of this document: http://www.ihmc.us/users/phayes/IKL/GUIDE/GUIDE.html
Abstract
Introduction
Logic for Interoperability
Frameworks
IKL is not segregated
IKL is transparent
IKL is panoptic
IKL is not indexical
IKL is monotonic
IKL is unsorted
IKL Overview
Forms of quantifiers
Special IKL name forms
Using quoted strings as indirect names
Proposition names
Proposition names are referentially transparent
Identity between propositions
Datatyping
Translating other logics into IKL
Keeping track of names
Description logics translate into IKL relational operators
Sorts become legality classes in IKL
Contexts and Modalities in IKL
Introduction
Fixing the base context
Indexical sentences map into IKL propositions related to a context
Opaque contexts are rendered using opaque names
Eliminating ist
Putting contexts into atomic sentences
Examples
Footnotes
Appendix A: IKL structural axioms
Equalities
Patterns of Variadicity
Sequence markers vs. argument lists
Description Logic constructions
Operations on Propositions
Appendix B: More on Propositions
Identity Conditions for Propositions
The liar paradox and other exotica
References
This is a description of IKL, the IKRIS Knowledge Language, intended as a general guide and overview, with an emphasis on how to represent in IKL a variety of ontological devices found in other notations. For the formal syntax and semantics of IKL see the IKL Specification document [IKLSPEC].
IKL is a logical formalism designed for interchange and archiving of information in a network of logic-based reasoners. IKL is extremely expressive and can represent the same content as a wide variety of formal notations, but it has a simple 'classical' logical semantics and can be processed by conventional first-order logic engines. IKL is a variant of the CLIF dialect of ISO Common Logic [CL], extended with terms which denote propositions and a device for relating names to the character strings which are used to indicate them. Common Logic is a proposed ISO standard for a general-purpose first-order information exchange language, based loosely on KIF [KIF]. The design rationale for CL is explained in [CL]; in summary, it is designed to remove or avoid as many restrictions as possible on what can be said in a first-order language, and to facilitate knowledge interchange across a network. IKL follows in the same tradition. IKL achieves its unique expressiveness from its ability to quantify over the propositions expressed by its own sentences, which in effect allows it to be its own meta-language, so it can bring the full expressive power of logic to the task of talking about propositions as well as simply expressing propositions by sentences. This single device can replace a wide variety of 'alternative' logics, including modal, context, temporal and indexical logics, by various ontologies all written in a single logical framework, which facilitates interoperation..
The next section describes the general philosophy behind the design
of the logic (much of it inherited from Common Logic); the next section
describes the logic itself, the basic syntactic devices available, and
finally we outline some ontology construction techniques. Throughout
this document IKL examples are written in this format; other formal languages are written in this format.
A familiar principle in formal language design is that a notation should be compositional: the meaning of an expression should be built up from the meanings of its component expressions, and should be the same wherever it appears, so that expressions with identical meanings should be interchangeable with one another wherever they occur. IKL is compositional in this sense, but in addition it extends this idea to an entire communication network. A central presumption underlying the design of IKL (and CL) is that when IKL expressions are transmitted across a network or archived for later use, their meaning should be the same at the point of use as it was at the point of origin, no matter how remote these are from one another. What this means in practice is that IKL expressions – both names and sentences – retain their meaning regardless of the enclosing theory or context in which they are stored, transmitted, asserted or used. This has several significant consequences.
Since the primary purpose of IKL is to act as an interlingua to
provide for translation between other notations and systems, it is
useful to be able to refer to such systems explicitly. We use the term framework
to refer to any such systematically organized system of assumptions,
notational conventions or background assumptions, and the IKL class name
Framework to indicate them. All of the alternative
notations or ontological settings from and to which IKL can be
translated are considered to be frameworks. There is no exact theory of
frameworks, but the term enables various conventions used in IKL to be
related to one another and contrasted with others. Frameworks often have
an associated vocabulary, in some cases a distinct namespace in the XML
sense. Examples of frameworks include the XML Schema datatype
conventions, the Dublin Core vocabulary, non-IKL logics such as ICL or
IODE, and specialized representational frameworks such as PSL [PSL].
IKL follows CLIF in allowing any name to be used in any way, and treats all names as denoting things: in Common Logic terms, it is not a segregated dialect. This means that there is no logical distinction in IKL between classes and individuals, or between relations and particulars: relations and classes are first-class entities which may themselves be in classes, take part in relations, and so on, with perfect freedom, and one can write axioms which quantify over them, so can speak of a class of classes, and write axioms about all the classes in a certain class of classes, etc.. Although IKL is a first-order logic, the resulting syntactic freedom allows for a great deal of expressive improvement over a conventional first-order syntax.
What this means in practice is that any collection of well-formed IKL sentences is itself well-formed: one can mix and combine IKL content with complete freedom, without needing to perform lexical checks for possible syntactic inconsistencies between incompatible uses of a name.
Different frameworks may use the same name to refer to different things. For example, datatypes impose fixed meanings on particular character sequences, which may differ from the meanings one gets by using them as names: 12 is twelve, but '12' means ten in octal. Again, assertions which represent someone's beliefs may use names in ways which reflect the believer's misunderstandings rather than what a name actually refers to. When such frameworks are put together, some device must be used to keep track of the various name uses. Many of the traditional logical devices result in opaque constructions, in which the same name has different meanings when used in different sentences or expressions. Opaque logics cannot be used with conventional reasoning strategies and require specially modified logical reasoners, and the contextual nature of name usage in these logics makes them inherently unlike a network logic. IKL is a wholly transparent logic where all expressions have a single referent and equality reasoning can be used freely. To achieve the needed flexibility of name use, IKL uses a variety of quoted name conventions rather than using names differently in different contexts. These conventions, which all use functions applied to quoted character strings, generalize and extend datatyping schemes which are widely used in applied ontology work and have proven robust and powerful.
IKL is panoptic in the sense that it assumes a single universe of discourse over which all quantifiers range, and which contains all things which are in all 'local' or 'contextual' universes of discourse. If it were not, the meaning of a quantified sentence could change when the sentence is moved across the network. Since different frameworks may be based on different assumptions about what kinds of things exist, their translations into IKL must make these assumptions explicit, usually by restricting quantifiers to elements of a particular IKL class representing the 'local' universe of the framework. [*2]
A byproduct of being panoptic is that even the logic's own expressions and propositions are considered to be part of the universe of discourse. IKL can refer to the character strings which comprise its own names, and to the propositions expressed by its own sentences.
An indexical expression is one in whose meaning depends on the circumstances or context of use. Words like here, now, you and so on make English an indexical language. IKL is not indexical. To see intuitively why an interchange language cannot be indexical, imagine recording facts about the present time using a word like now, and storing them for later use in this form, so that the fact that it is raining at some time would be recorded literally as raining now; and then this stored fact is retrieved from memory at some future date. Clearly it has changed its meaning, since now at the time of retrieval does not refer to the same time as now when the information was archived. Tensed language suffers the same fate, since references to the future will need to become references to the past. Similarly, geographically sensitive information cannot be transmitted to another location using spatial indexicals such as here. In general, the correct way to encode indexical information into IKL is to replace the indexicals with identifying information which uses some kind of global temporal, spatial or other contextual reference framework whose meaning is universally agreed upon, and will remain stable. The IKL quoted-name conventions provide a general-purpose technique for relating name meanings to such reference frameworks.
Although it provides for the expression of contextual and time-dependent propositions, IKL is not a context or temporal or modal logic, since such logics are inherently indexical. Sentences of IKL should not be understood to be asserted 'in' an implicit context or belief framework, or 'at' a time of utterance. All such relativizations of assertion or truth must be de-indexed in IKL by referring explicitly to the context, belief state, time-interval, etc.., relative to which they are intended to be understood. Similarly, the meaning of any IKL sentence is not dependent on that of other IKL sentences, so does not change when it is moved from one logical theory or context to another.
Similarly, names used in IKL are understood to refer to their referents in a single referential framework: they do not change their referents when used in a different context or setting. Any such variations in reference must be made explicit in IKL, for example by the use of functions from contexts to referents.
Like most conventional logics, IKL is monotonic, so that inferences
made from information expressed in IKL sentences remain valid when new
information is added. However, unlike most conventional logics, IKL is
capable of expressing the conditions that are often cited to justify
non-monotonic reasoning, as explicit IKL axioms. For example, a
unique-name assumption, that any two distinct names in a certain set Base of names must denote distinct entities, can be axiomatized in IKL by writing:
(forall ((x charseq)(y charseq))
(if (and (Base x)(Base y)(not (= x y))) (not (= (tnb x)(tnb y)))
)
The quantification here is over the lexical forms of the names
themselves, rather than (the more usual case) over the things that the
names denote; however, those denoted things are also referred to here by
calling the name as a function. The IKL function tnb ('thing
named by') maps a character string to whatever that string would denote
if used as a name. This simple 'dequoting' device allows IKL to
straighforwardly describe many conditions that are inexpressible in a
conventional logic.
A sorted logic or notation treats the universe of discourse as divided up into special classes or categories, called sorts or types, treating these as defining syntactic constraints, so that any expression which would violate these conditions as being a syntactic error, detectable by a parser, rather than a logical inconsistency. [*3]
IKL is not a sorted language in this sense, since there is never likely to be universal agreement between frameworks on what constitutes a 'nonsensical' assertion. While IKL therefore does not impose any syntactic restrictions on what can be said, it does allow for the expression of these restrictions as semantic classifications, described axiomatically, thereby allowing the restriction to be applied by a reasoner rather than by a parsing mechanism. The general technique is described in later sections.
For interoperation purposes, what is usually necessary is simply to be able to check that some expression is 'legal' according to a framework's rules, before sending the appropriate translation of the IKL content to an engine which is expecting input according to the rules of that framework. This can be done in IKL by normal logical reasoning.
Ths section summarizes the main features of IKL syntax and semantics. Details are relegated to footnotes where possible.
IKL syntax is based on CLIF, the KIF-like syntax defined for ISO Common Logic. For a full description of CLIF syntax, see [CL]. Briefly: it looks like a conventional logic, except that atomic sentences and terms are written in 'Lisp style', with the relation or function name after the opening parenthesis, and with names separated by whitespace rather than commas. This same style is used for the quantifiers and connectives, which are always written as prefixes rather than as infixed, so that one gets things like
(forall (x y) (if (and (Married x y)(Male x))(Female y)) )
rather than
forall (x, y) ( (Married(x,y) and Male(x)) implies Female(y) )
or
(x):(y):. Married(x,y) & Male(x) : => Female(y)
The only 'formatting' characters used in IKL syntax are the parentheses and whitespace, although the single and double quote marks, the backslash character, and the ellipsis (three consecutive dots) all play lexical roles.
IKL has the usual connectives[*4] :
not |
negation, takes a single argument |
and |
which can have any number of arguments, including zero: (and) is the truth-value true. |
or |
similarly: (or) is the truth-value false. |
if |
implication, takes precisely two arguments. This is written '=>' in KIF. |
iff |
|
and the two basic quantifier forms:
exists |
existential |
forall |
universal |
A single quantifier can bind a sequence of names, written enclosed in parentheses, as in the above example. All quantifiers must be made completely explicit in IKL: there are no 'implicit' quantifier conventions used by some languages. Unlike KIF, IKL has no special notation for 'variables'. Any name may be bound by a quantifier. [*5]
IKL follows Common Logic in allowing any name to be used as a relation or function name, which allows relations and functions to be quantified, and allowing terms to denote relations and functions, and allowing relations and functions to take any number of arguments. In these respects Common Logic and IKL have much of the intuitive flavor of a higher-order logic, while retaining the semantic and computational properties of a first-order logic.[*6] IKL extends this syntactic freedom to also allow any name to be used to denote a proposition, and any character string to be used as a name. These extensions, described in more detail in later sections, give IKL enough expressive power to represent the knowledge expressed in any other KR formalism, often in a more compact form.
IKL also follows Common Logic in allowing arbitrary degrees of commenting to be attached to expressions. Any IKL expression, even those deeply nested inside other expressions, may be 'wrapped' with a comment, by substituting
(comment <comment string> <expression> )
for the original <expression>. This applies to names, terms, sentences and even whole chunks of IKL text containing multiple sentences; and it also applies to the commented sentences themselves, so that one can have 'layers' of comment wrappers. As far as the actual IKL logic is concerned, all such comments are invisible and have no effect upon the meaning; but IKL engines are required to preserve them while parsing and transmitting IKL text. The comment string can be any IKL quoted string (see below), which allows any Unicode text to be used as a comment.
At the very topmost syntactic level, IKL text consists of a sequence of sentences, any subsequence of which may be wrapped in a comment. This allows 'bare' comments which wrap an empty text sequence to be inserted between sentences, and groups of sentences to be commented together. Finally, an alternative top-level item in IKL text is an importation of the form
(import <identifier>)
where <identifier> has to be understood a 'network name' — typically, a URI — which can be used to identify some other IKL text, with the intended meaning that this identified text is to understood to be asserted as part of the text where the import occurs, just as though it were copied there explicitly. This allows IKL text to include content from other IKL texts.
Texts may be named by preceding them with a declared name, or by using external naming conventions. The name of a text is understood to denote the actual IKL syntax of the text, considered as a character sequence; since character sequences are first-class entities in the IKL semantics, this means that IKL texts can be treated as first-class objects, so that one can express relationships between texts, properties of texts, etc., and write axioms which refer to IKL texts. Attaching an identifier to a text as its name is assumed to create a rigid naming relationship between the identifier and the text, so that assertions made using the name to refer to the text may be checked by examining the text itself.
IKL allows for a variety of elaborated quantifier forms.
Quantified names can be restricted by bracketing them with a restriction in the quantifier binding:
(forall ((x isHuman))(exists ((y charseq))(= y (nameOf x)) ))
which is an abbreviation for
(forall (x)(if
(isHuman x)
(exists (y)(and
(charseq y)
(= y (nameOf x))
))
))
Restrictions on quantifiers are usually simple class names, as above, but they can be terms. Each restriction can be applied only to a single binding, but restricted and unrestricted bindings may be used in a single quantifier:
(forall ((x isHuman)(y isHuman) z) ... )
Not *** (forall ((x y isHuman) z) ... ) ***
Numerical quantifiers are indicated by a non-zero numeral[*7] immediately following the quantifier:
(forall ((x isHuman))(exists 10 (y) (and (Toe y) (PartOf y x)) ))
Numerical quantifiers can bind only a single variable. This is not legal: [*8]
Not *** (exists 3 (x y) ... ) ***
But the variable can be restricted, so this is OK:
(forall ((x isHuman))(exists 10 ((y Finger))(PartOf y x)))
which is equivalent in meaning to a sentence of the form:
(forall ((x isHuman x))...
(exists ((y1 Finger)(y2 Finger) (y10 Finger)(and...
(allDifferent y1 y2 y10)...
(PartOf y1 x)
(PartOf y2 x)
(PartOf y10 x)
))
)
This does not say that humans have ten parts, or even that they
have only ten fingers: it says that for each human, ten (distinct)
fingers exist, i.e. that humans have at least ten fingers. (The relation allDifferent, which can take any number of arguments, is defined below.)
Finally, IKL follows Common Logic in allowing quantifiers to bind sequence markers in addition to names.[*9] A sequence marker (called a sequence variable in KIF, and written with the prefix @),
used as an argument to an atomic sentence or term, stands for an
arbitrary sequence of arguments, and may be bound by a quantifier. IKL
uses the ellipsis mark ... (possibly followed by some other characters) as a sequence marker[*10].
The effect is to allow a form of recusive definition in IKL which
allows a single sentence to express an infinite number of cases. It is
best explained by an example. Suppose we want to define a relation allEqual which is a 'variadic equality', so that
(allEqual "Osama bin Laden" "Usama bin Laden" Oussama_Bin_Laden "Osama Binladen")
is a shorthand for
(and
(= "Osama bin Laden" "Usama bin Laden")
(= "Osama bin Laden" Oussama_Bin_Laden)
(= "Osama bin Laden" "Osama Binladen")
)
and similarly for any number of arguments. (Double-quotes are used
when a name contains spaces or other lexical break characters; these are
called enclosed names.) This can be described recursively: (allEqual a b ... a sequence of arguments) is true when (= a b) and (allEqual a ... the same sequence of arguments) are both true, for any sequence of arguments. This transcribes directly into the IKL:
(forall (x y ...) (iff (allEqual x y ...)(and (= x y)(allEqual x ...)) ))
Note that all occurrences of the sequence marker indicate the same
sequence; in this respect a sequence marker acts just like a name. The
inference rule for sequence markers is that a universally quantified
sequence marker can be replaced by any finite sequence of terms (compare with the usual rule for universally bound names, which can be replaced by a single
term.) Note that the empty sequence is one case of this. Using this
rule, the above universal sentence has these instances, intuitively
obtained by recursively 'calling' the definition on each occurrence of allEqual in the previous instance, shown in bold face:
(iff
(allEqual "Osama bin Laden" "Usama bin Laden" Oussama_Bin_Laden "Osama Binladen")
(and (= "Osama bin Laden" "Usama bin Laden")(allEqual "Osama bin Laden" Oussama_Bin_Laden "Osama Binladen"))
)
(iff
(allEqual "Osama bin Laden" Oussama_Bin_Laden "Osama Binladen")
(and (= "Osama bin Laden" Oussama_Bin_Laden)(allEqual "Osama bin Laden" "Osama Binladen"))
)
(iff
(allEqual "Osama bin Laden" "Osama Binladen")
(and (= "Osama bin Laden" "Osama Binladen")(allEqual "Osama bin Laden"))
)
The last was obtained by substituting the empty argument sequence for the sequence marker, i.e. in effect simply by erasing it, at which point the recursion stops. This shows that we also need to state the 'trivial' empty-sequence case as part of the definition:
(forall (x) (allEqual x))
with which, and stitching together the three above instances, we get the required equivalence. This general pattern, of a universally quantified recursive definition with a special axiom covering the trivial empty-sequence case, is typical of how sequence markers are used in IKL.
Two further examples:
(forall (x y ...) (iff
(allDifferent x y ...)
(and
(not (= x y))
(allDifferent x ...)
(allDifferent y ...)
)
))
(forall (x)(allDifferent x))
This definition (due to Chris Menzel) defines an 'elastic inequality', and illustrates the use of a double recursion to generate o(n|2) negated equations from n arguments. (This is a much stronger statement than merely denying allEqual. )
Another example:
(forall (p ... x)(iff ((OR p ...) x)(or (p x)((OR ...) x))) ))
This defines a function on unary relations corresponding to disjunction: for example (OR American Mexican Canadian) is the property of being either American, Canadian or Mexican. Note the difference between the connective or, which like other connective names is a reserved word in IKL, and the function OR. The trivial empty case here is the case of no arguments:
(forall (x)(not ((OR) x) ))
Note the negation: the empty case of a disjunction is everywhere false. This example illustrates the use in IKL of a "higher-order" function on relations, and the ability to quantify over relations. [*11]
IKL has a variety of pre-defined name forms, with fixed meanings.
The simplest of these are decimal numerals (which denote non-negative
numbers) and quoted strings (which denote Unicode character sequences).
The corresponding predicates or class names are number and charseq respectively:
(number 342)
(charseq 'this is a character sequence')
Numerals may have leading zeros but otherwise are conventional. Quoted strings are written using single quote marks,
'like this'
They may contain any characters, including whitespace and parentheses. (To include a single-quote or backslash character, precede it with a backslash; to include a non-ascii character, write its 4-digit hexadecimal Unicode sequence preceded by a backslash.[*12] ) The quoted string denotes the character sequence gotten by replacing all backslashed codes by their Unicode equivalents and then removing the backslashes and surrounding single quote marks. For example,
'\0395\03BB\03BB\03AC\03B4\03B1' denotes the 6-character Unicode sequence 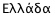 .
.
Quoted strings are must be carefully distinguished from names written using double quote marks, called enclosed names, as illustrated earlier with "Osama Binladen".
Although similar lexical conventions apply in the two cases, enclosed
names are simply a lexical device to allow a normal IKL name to be
spelled using whitespaces, parentheses, etc.. They function logically
just like any other name. Quoted strings, in contrast, are not logical names, because they have a fixed meaning. '\0395\03BB\03BB\03AC\03B4\03B1' denotes a particular sequence of six Unicode characters, and cannot mean anything else; in contrast, "\0395\03BB\03BB\03AC\03B4\03B1" is the name of Greece rendered in Greek characters, and could be used to refer to the country.[*13]
Although names and quoted strings are distinct, there is an obvious relationship between them: IKL quoted strings denote Unicode character sequences, and IKL names are Unicode character sequences. That is, quoted strings denote names. IKL takes advantage of this with a special indirect naming convention whereby calling a character sequence as a function with no arguments gives you whatever the name corresponding to the character sequence[*14] refers to, as the function value. This is easier to illustrate then it is to describe. It means that a very simple term formed by putting parentheses around a quoted name must refer to whatever the name refers to when unquoted:
(= Chris_Menzel ('Chris_Menzel'))
(= JohnSowa ('JohnSowa'))
(= "Chris Welty" ('Chris Welty'))
since the surrounding parentheses amount to writing a term which has that character sequence as the function and no other arguments. Thus, IKL has two ways to refer to anything: by using a name directly, or by referring to the character sequence of the name and 'calling' it to deliver the named referent.
As an aid to readability, we define a function tnb (thing named by) from character strings to referents:
(forall ((x charseq))(= (tnb x)(x) ))
so that (tnb 'Selene_Makarios') is Selene_Makarios.
Using the explicit function rather than the basic convention is not
necessary, but can sometimes make formulae more readable. A term of the
form (s) or (tnb s), where s is a quoted string, is an indirect name which corresponds to the name gotten by using the character sequence itself as a name: (tnb 'Foo') is the indirect name corresponding to the name Foo. Other names can be used, of course: for example
(= referent tnb)
Indirect names are the simplest form of a convention widely used in IKL, whereby references are made indirectly by using character strings to denote names which then, in turn, refer to things in the universe. This indirect reference allows for a variety of naming conventions to be decribed, inter-related and used together in a single transparent logical framework, and allows IKL to efficiently model a variety of opaque naming conventions.
Examples of this general technique are used for datatyping (in which a datatype function is applied to a character string, to indicate an interpretation fixed by some naming convention) and for expressing contextual interpretations of name referents (in which the quoted name is applied to the context, as a form of 'contextual subscripting').
IKL's most significant extension to Common Logic is its provision
for referring to its own propositions. This is done by a syntactic form
which makes a sentence into the name of the corresponding proposition,
by enclosing it inside parentheses, preceded by the special IKL reserved
word that. The resulting expression is called a proposition name. For example:
(that (isHuman Deborah_McGuiness))
denotes the proposition that Deborah_McGuiness is human. Any IKL sentence, of any degree of complexity, may be used to form a proposition name:
(that (and
(forall (x ... y)(iff ((AND x ...) y)(and (x y)((AND ...) y)) ))
(Mellifluous butterscotch)
))
and the proposition so named is always the proposition expressed by the enclosed sentence.
In a sharp contrast to quoted strings, the 'inner' names of the sentence are still visible to other operations, and can for example be bound by quantifiers:
(exists (x)
(believes Bill_Andersen
(that
(and
(Iranian x)
(customer x "Bank Melli Iran")
(exists 3 ((y aircraft))(owns x y))
)
)
))
This attributes to Bill a belief about an un-named, but real, Iranian. Contrast this with the much weaker:
(believes Bill_Andersen
(that
(exists ((x Iranian))(and
(customer x "Bank Melli Iran")
(exists 3 ((y aircraft))(owns x y))
)))
)
which simply says that Bill believes that some such Iranian exists, and is not a belief about anyone in particular.[*15]
It is important to distinguish between a proposition name and the sentence it contains. Although they 'say the same thing' in an intuitive sense, one cannot write a proposition name in place of a sentence, or vice versa, since they play distinct syntactic and semantic roles in the IKL logic. Writing a sentence asserts it to be true, but a proposition name simply refers to the proposition, and does not assert anything about it. One uses a proposition name in order to say something about the content of a sentence — for example, that it is believed by someone, as in the above examples, or is true under certain circumstances or only in a certain context, or is considered to be reliable, or was derived from a certain source — rather than to simply assert it as a fact.
To say that a proposition is true, think of it as a relation with no arguments, and write an atomic sentence with that relation applied to an empty argument sequence, i.e. the proposition name simply enclosed in a pair of parentheses. For example
((that (isHuman "Brant Cheikes")))
is such an atomic sentence, which means exactly the same as the inner sentence of the proposition name:
(isHuman "Brant Cheikes")
This works for any proposition, no matter how complex its expression. The following
((that
(exists ((x Iranian))(and
(customer x "Bank Melli Iran")
(exists 3 ((y aircraft))(owns x y))
))
))
(note the 'extra' pair of outer parentheses) is an atomic sentence, of the form (r) where r
is a proposition name, which therefore asserts that the proposition is
true; which is of course exactly what one would assert by simply writing
the inner sentence as a sentence in its place:
(exists ((x Iranian))(and
(customer x "Bank Melli Iran")
(exists 3 ((y aircraft))(owns x y))
))
One can, therefore, think of the process of enclosing a sentence inside (that ...)
as reifying the content of the sentence — making it into a 'thing' —
and then applying extra parentheses which form an outer atomic sentence
as 'cancelling' or reversing this reification to get the sentence back
again:
((that
(exists ((x Iranian))(and
(customer x "Bank Melli Iran")
(exists 3 ((y aircraft))(owns x y))
))
))
In the spirit of Common Logic, any name may be used to denote a proposition: in fact, one can think of IKL propositions as simply being Common Logic zero-ary relations. Since propositions are first-class objects, they can be quantified over in the usual way, so one can write general axioms about propositions. For example, we can define a function on propositions corresponding to disjunction, similarly to the one defined earlier for unary relations. In fact, the definition is obtained from that one simply by erasing the relational argument, since a proposition is treated as a zero-ary function. The 'cancelling' outer parentheses which take a proposition name into an atomic sentence are written here enlarged and in bold for clarity.
(forall (p ... )(iff ((OR p ...))(or (p)((OR ...))) ))
Note that p is a name being used here to refer to propositions; OR is a function,(OR p ...) and (OR ...) are terms – not sentences – also denoting propositions; while ((OR p ...)), (p) and ((OR ...)) are atomic sentences which assert the propositions they contain.
Note that it would be incorrect to write this axiom without the outer calling parentheses:
Not *** (forall (p ...)(iff (OR p ...)(or p (OR ...)) )) ***
since the name p cannot be used as a sentence. Names in IKL can only denote or refer to things: sentences make assertions.
Readers whose eyes glaze over at this LISP-style plethora of nested parentheses can use an explicit isTrue truth predicate on propositions, which has the trivial definition:
(forall (p)(iff (isTrue p)(p) ))
and then the 'cancellation' rule can be stated thus:
(isTrue (that <sentence>)) is equivalent to <sentence>
and the definition of OR for propositions given above can be written as:
(forall (p ...)(iff (isTrue (OR p ...)) (or (isTrue p)(isTrue (OR ...)) )))
When this convention is used, proposition names occur only as arguments of other relations.
Names which occur free inside a proposition name all refer in the same way as they do in other IKL sentences. This means that proposition names, like the rest of IKL, are referentially transparent. For example, if
(= Bill William)
then it follows that propositions about Bill are also about William, since they are about the same thing no matter what name is used to refer to him:
(= (that (Happy Bill)) (that (Happy William)))
and hence
(iff ((that (Happy Bill)))((that (Happy William))) )
Since the names occurring inside a proposition name are understood to have the same references that they have in normal IKL text, one can bind them with quantifiers in the same way. This allows 'quantifying in' to a proposition term:
(exists ((x isHuman)) (Believes "Lois Lane" (that (= x Superman)) ))
This transparency has some consequences for using propositions to
represent psychological states of belief, where the believer may be
using names to refer differently from the rest of the logic. We discuss
this in greater detail below: for now, however, note that transparency
means for example that if Bill is in fact the same as William, and
(Believes Harry (that (isLiar Bill)))
then it follows – in fact, it is the same assertion – that
(Believes Harry (that (isLiar William)))
and this holds whether or not Harry knows Bill by his other name. This follows from the transparent and panoptic nature of IKL: names inside propositions mean the same – refer to the same thing – without being influenced by any surrounding context of belief in which the proposition might be placed.
Proposition names are different whenever they use different sentences, but it is reasonable to claim that 'trivial' changes in the inner sentence should not require the proposition names to denote distinct propositions. For example, it seems clear that
(that (forall ((x isHuman))(isMammal x)))
is the same proposition as
(that (forall ((y is Human))(isMammal y)))
IKL has a special relationship of 'propositional identity', written =p,
to express this idea that two proposition names identify the 'same'
proposition. This is a delicate matter, since we want this to mean more
than being expressed by the same sentence but less than being logically
equivalent, and we want to be able to check the truth of =p between two propositon names by a reasonably fast computation on the inner sentences. The full account of =p is based on work by John Sowa [SOWA] and is given in Appendix B, along with more advanced topics concerned with proposition names, defining propositions and "paradoxical" constructions.
The IKL conventions for numbers and character strings can be seen as special cases of a general technique which mirrors the notion of datatyped literal used in RDF [RDF] and OWL [OWL]. This provides a uniform method for describing various standardized naming conventions.
A datatype is a framework, typically encoding some
conventional naming standard, which associates values with certain
character sequences. Examples include various forms of numerals (octal,
hexadecimal), calendar dates, formats for representing clock times,
geographical coordinate systems, etc.. For example, number and charseq
can be regarded as built-in IKL datatypes. A datatype name is used in
IKL in three ways: to refer to the datatype framework itself, as a
property which is true of the legal values, and as a function from
character sequences to their characteristic values in the framework. To
illustrate, using number as the datatype name:
(Datatype number)
number is a datatype. This uses the name to refer to the datatype itself.
(number 345)
(not (number '345'))
Three hundred and forty five is a number; the character sequence '345' isn't. This uses the datatype name as a predicate or a class name.
(= 345 (number '345'))
(number (number '345'))
The term (number '345') uses number as a
function from character strings to numbers: the second assertion uses
the name both as a function and as a property. This pattern gives the
characteristic axiom for 'legal' datatype strings:
(forall ((x datatype)(y charseq))(iff (legalCharSeq y x)(x (x y)) ))
For example, (not (legalCharSeq 'abc' number))
Notice that the datatype function always applies to a quoted
string. This treatment of datatyping is an exact mirror of the way that
datatyped literals are treated in RDF [RDF] and OWL [OWL], based on the treatment in XML Schema, Part 2 [XSD]. The lexical space of each datatype is the set of character sequences which are legalCharSeq for that datatype. The XML Schema datatype names are written with the conventional prefix xsd: in IKL. For example,
(xsd:dateTime '2002-10-10-T12:00:00-05:00')
refers to noon on 10 October 2002, US Central Daylight Savings Time.
The XML Schema datatypes define a variety of useful naming conventions for numbers and dates. As these datatypes are based on ISO standards and are already in wide use, users are encouraged to use them when possible rather than invent new or ad-hoc schemes, as an aid to interoperation.
This section outlines techniques for representing content from a variety of existing knowledge representation formalisms into IKL.
To support interoperability, IKL names used in translations should be related explicitly to the name used in the original framework. There are various ways to do this. The simplest is to re-use the same name in IKL as was used in the original framework, but this causes confusion when the same name is used in different frameworks, and does not provide any straightforward way to 'map back' from the IKL, since it does not identify the source framework explicitly.
In order to maintain coherence between a variety of naming
conventions and still preserve readability of the IKL sentences, we
recommend using new names in IKL axioms and relating them to the
original framework name explicitly, by extending the indirect naming
convention described earlier. For this purpose, IKL provides a function frameworkName which
maps a framework and a character sequence denoting the framework name
to the corresponding name used in IKL. For example, to say that psl:activity in the framework PSL maps to the IKL name EventType, include the name conversion axiom:
(= 'EventType' (frameworkName PSL 'psl:activity'))
as part of the translation from PSL to IKL. Such name conversion axioms are helpful even when the same name is used:
(= 'occurrence' (frameworkName PSL 'occurrence'))
To say that all the names in a framework are re-used without change, quantify over the character strings:
(forall ((s charseq))(= s (frameworkName PSL s)) )
To refer to the thing denoted by a name in a framework, apply tnb to the value of frameworkName:
(= EventType (tnb (frameworkName PSL 'psl:activity')))
Description logics (DLs) provide operations which can be used to define new 'classes' in terms of other classes and 'properties', both of which correspond to IKL relations: DL classes are unary relations - predicates - and DL properties are binary relations. The syntactic flexibility of IKL allows the operators to be axiomatized directly, as functions from relations to relations. To illustrate, we use the main constructions of the semantic web description logic OWL-DL. The formal definitions are in Appendix A. [*16]
Ground facts (often called 'A-box' sentences in the DL literature) such as membership in a class, or a property having a value, are represented as a simple atomic sentences such as
(isHuman "Osama bin Laden")
(childOf "Osama bin Laden" "Hamida al-Attas")
and relationships between classes and properties are expressed directly as assertions about the relations:
(IF isHuman isMammal)
(INVERSE childOf parentOf)
Description logics vary in their expressivity, but most contain operators corresponding to the Boolean connectives and, or and not,
which take classes into other classes, and some collection of
restrictions, which take a class and a property (and sometimes a number)
into a class, as in people who have at least three children all attending school in the USA, composed from the classes Person and School, the properties childOf, attends, locatedIn and the individual USA. [*17] Using the vocabulary defined in Appendix A this would be the IKL term:
(AND
Person
(ATLEAST 3 childOf)
(ALLARE childOf (SOMEARE attends (AND School (IS locatedIn USA)))))
)
Note, this is a term (denoting a relation, intended to be applied to a single argument), not a sentence. We could give this class a shorter name using an equation:
(= USTripleParent (AND Person (ATLEAST 3 childOf)
(ALLARE childOf (SOMEARE attends (AND School (IS locatedIn USA))))))
)
For comparison, the definition of this class in OWL/RDF/XML is:
<owl:Class rdf:ID="#USTripleParent">
<owl:intersectionOf rdf:parseType="Collection">
<owl:Class rdf:about="#Person" />
<owl:Restriction>
<owl:onProperty rdf:resource="#childOf" />
<owl:minCardinality
rdf:datatype="&xsd;nonNegativeInteger">3</owl:minCardinality>
</owl:Restriction>
<owl:Restriction>
<owl:onProperty rdf:resource="#childOf" />
<owl:allvaluesFrom>
<owl:Restriction>
<owl:onProperty rdf:resource="#attends" />
<owl:someValuesFrom>
<owl:intersectionOf
rdf:parseType="Collection">
<owl:Class
rdf:about="#School" />
<owl:Restriction>
<owl:onProperty
rdf:resource="#locatedIn" />
<owl:hasvalue
rdf:resource="#USA" />
</owl:Restriction>
</owl:intersectionOf>
</owl:someValuesFrom>
</owl:Restriction>
</owl:allValuesFrom>
</owl:Restriction>
</owl:intersectionOf>
</owl:Class>
The OWL/RDF/XML assertion of membership in this class:
<owl:Thing rdf:id="#Bill">
<rdf:type rdf:resource="#USTripleParent">
</owl:Thing>
translates into the atomic sentence
(USTripleParent Bill)
The operators AND, ATLEAST, etc., used to form the above term, are the IKL translations of the main syntactic components of the OWL language:
(= AND (frameworkName OWL 'intersectionOf'))
(= OR (frameworkName OWL 'unionOf'))
(= NOT (frameworkName OWL 'complementOf'))
(= ALLARE (frameworkName OWL 'allvaluesFrom'))
(= SOMEARE (frameworkName OWL 'somevaluesFrom'))
(= IS (frameworkName OWL 'hasvalue'))
(= ATLEAST (frameworkName OWL 'minCardinality'))
Relational terms can be used directly, simply by being placed in the relation position of an atomic sentence. For example
((OR (IS brother Joe)(IS brother Sally)) Bill)
captures in a single atomic sentence the exact same meaning as the disjunction
(or (brother Joe Bill)(brother Sally Bill))
In general, description logics map into collections of such functions which take unary and binary relations as arguments and denote new relations — usually unary relations, corresponding to DL classes — as value. Each description logic framework has a particular set of such 'relational functions' associated with it; in most cases this will be a subset of the OWL vocabulary. In many cases they come with restrictions on their use, which guarantee that various entailment relationships are decideable withing a reasonable complexity bound. While IKL does not impose any such restrictions itself, the fact that they apply can be annotated by suitable comments attached to the IKL translations.
A sorted logic or notation treats the universe of discourse as divided up into special classes or categories, called sorts, and relations (and functions) as having their domains and ranges restricted to combinations of these categories, and treats these as syntactic constraints, so that any expression which would violate these conditions – for example, by adding a numeral to a human being:
(plus 17 "Valeria de Paiva")
would be rejected by the parser as a syntax error.
While IKL does not impose any syntactic restrictions on what can be said in it, it does allow for the expression of these restrictions as semantic classifications, described axiomatically, thereby allowing the restriction to be applied by a reasoner rather than by a parsing mechanism. The strategy described here can be used to axiomatize most sort-checking frameworks in IKL. For many purposes of translation between frameworks, however, such translation may not be required, and it may be sufficient simply to declare that certain class names are considered to be sort categories. For interoperation purposes, the most that is usually necessary is simply to be able to check that some expression is 'legal' according to a framework's rules, before sending the appropriate translation of the IKL content to an engine which is expecting input according to the rules of that framework.
The simplest way to translate sorts into IKL is to treat the sorts as classes, i.e. unary relations, state their exclusion conditions explicitly, and to restrict quantifiers to these classes as appropriate:
(Human CharlesKlein)
(Integer 17)
(forall ((x Human))(not (Integer x)))
(forall ((x Integer))(not (Human x)))
(forall ((x Integer)(y Integer))(Integer (plus x y)) )
It is straightforward to define some useful abbreviations which make this less tedious:
(forall (x y)(iff (disjoint x y)(not (exists (z)(and (x z)(y z)))) ))
(forall (x y z ...) (iff
(disjoint x y z ...)
(and (disjoint x z ...)(disjoint y z ...)) ))
(disjoint Human State City Integer)
The above technique maps any sort error into a logical inconsistency, so it does not distinguish between sort errors and other contradictions. For many purposes, therefore, it is more useful to be able to infer that a sort error of a particular kind has occurred. This requires a rather different style of IKL axiomatization. Since a situation may be an error in one framework but not in another, we need to refer the error to the framework which forbids it, by 'allowing' the error to occur consistently — that is, not generating an inconsistency from a sort error, but instead ensuring that an assertion is provable to the effect that it is that particular kind of error. In this kind of axiomatization, then, 'impossible' things like human numbers are considered to be logically possible, so that they can have properties, but are classified as 'excluded' or 'bad' according to the framework. Disjointness of two sort categories has to be expressed by saying that anything in their intersection is bad; that a function requires arguments of a certain sort is expressed by saying that its value when applied to any other kind of thing is bad; and that a relational argument must be of a certain sort is expressed by saying that anything not in that category of which the relation is true, is bad. Fixing the arity of a function - the number of arguments it is allowed to have - is done by asserting that the result of applying it to any other number of arguments is bad. Badness is then a property of things, whose provable presence in the universe of discourse is a symptom of the assertion of a type error of some kind.
To do all this in a uniform way requires that we agree on some basic vocabulary. The function SortInFramework takes a framework to a predicate on classes, which is true for classes which correspond to the sorts of that framework, and disjointFor takes a framework to a relation between classes corresponding to the simple disjoint. Similarly, SortErrorInFramework
takes a framework to a predicate which holds of entities which exist in
IKL but which would be excluded from the framework by virtue of its
sortal rules on wellformedness: for example, the entity resulting from
adding 17 to PatHayes might be such a thing. (Since in IKL all functions are total on the whole universe, this entity must exist, although it might not be very interesting.)
For example, suppose that a certain framework, called Frob, recognizes human, integer and realnumber as disjoint sorts and requires a distinction to be made between integer and real addition, and wishes these to be used only as binary functions. We can describe Frob's syntactic sort constraints by the following IKL text .
(text
(comment
'This is the key assertion which "triggers" the rest of the theory.
It can be viewed as placing Frob in a certain special class, whose
elements are constrained by these axioms.'
(Framework Frob)
)
(comment
'This defines a binary disjointFor. Rather than logically
forbidding anything to be in the intersection of two sorts, it asserts
that anything in that intersection is a sort error. This axiom
illustrates that a term used as a quantifier restriction may itself
contain a name bound by another quantifier.'
(forall((f Framework) (c (SortInFramework f))(d (SortInFramework f)) x)
(if (and ((disjointFor f) c d)(c x)(d x))((SortErrorInFramework f) x)
))
)
(comment 'This extends the binary disjointFor to more than two arguments.'
(forall ((f Framework) x y z ...)(iff
((disjointFor f) x y z ...)
(and ((disjointFor f) x z ...) ((disjointFor f) y z ...))
))
)
(comment 'Being a "proper" member of a sort category is subtler
than simply being in the sort class itself. For example, if something is
both human and an integer then it is in the class of integers but is a
sort error, so is not a kosher member of the sort integer.'
(forall ((f Framework) (c (SortInFramework f)) x)
(iff ((OfSortIn f) c x)(and (c x)(not ((SortErrorInFramework f) x)) ))
)
(comment 'The next three axioms introduce abbreviations to save typing.')
(= FrobSort (SortInFramework Frob))
(= FrobBad (SortErrorInFramework Frob))
(= OfFrobSort (OfSortIn Frob))
(Predicative FrobSort FrobBad)
(FrobSort human integer realnumber)
((disjointFor Frob) human integer realnumber)
(comment 'this is the simple positive half of the Frob sorting rule'
(forall ((x integer)(y integer))(integer (integerplus x y)))
)
(comment 'this is the negative or "only if" half, which in effect transmits sort errors from arguments to the value.'
(forall (x y) (if
(not (and (OfFrobSort integer x)(OfFrobSort integer y)))
(FrobBad (integerPlus x y))
))
)
(comment 'We can ensure that the function has a fixed arity by
saying that its value with any other number of arguments is an error.
Notice the use of three arguments plus a sequence marker to indicate
"three or more"'
(forall (x)(FrobBad (integerPlus x)(realPlus x)))
(forall (x y z ...)(FrobBad (integerPlus x y z ...)(realPlus x y z ...)))
)
(forall ((x realnumber)(y realnumber))(realnumber (realplus x y)))
(forall (x y) (if
(not (and (OfFrobSort realnumber x)(OfFrobSort realnumber y)))
(FrobBad (realPlus x y))
))
(comment 'end of text'))
The presence of a sort error, which in Frob would be detected by
the parser, is then indicated by the axioms entailing an assertion of
the form (FrobBad ...). For example, if
(Human Selmer_Bringsjord)
then
(FrobBad (integerplus Selmer_Bringsjord 17))
The effect of the Frob sort-checking parser can be obtained here by a dedicated 'greedy' reasoner which pays particular attention to assertions about Frob sort categories and attempts to prove the goal
(exists (x)((SortErrorInFramework Frob) x))
whenever new information is added. This reasoner can use essentially the same algorithm as the Frob parser would use, since it has access to the same information, although expressed here as assertions about sorts rather than meta-level declarations.
Modal and hybrid logics extend conventional logic by adding modalities, which take a sentence and 'shift' its truth-conditions in some way; for example, by asserting that it holds during a time-interval, or at a particular time, or in some possible circumstances; or that is is believed by someone, or that is derived from some knowledge source or authority. Context logics, a more recent invention, reduce all of these to a single uniform notion of truth in a context, and describe times, beliefs and so on as different kinds of context. As the context style of expression is capable of rendering the content from all such logics, we will treat modal and hybrid logics here as species of context logic, and describe all the translations as mappings from context logics to IKL.
There are many possible context logics, and the details of the translation depend more on the ontological assumptions underlying the particular logic than on its formal semantics.
Modal and context logics differ from IKL by being inherently indexical, so that even a simple (or unmarked) sentence – one stated without using modalities or context references in its syntax, so it looks just like an IKL sentence – is always understood to be asserted in an implicit 'local' context or setting. For example, in a modal tense logic, a simple assertion is understood as saying that the asserted sentence is true at the present time, or at the time of speaking. Similarly, the context logic ICL understands simple assertions to be asserted in a special 'identity context'. This means that even a simple sentence without modalities will differ in meaning, when asserted in a modal logic, from the same sentence asserted in IKL; and similarly for a simple sentence asserted without any contextual qualification, when asserted in a context logic. For example, take the sentence
(Dead Osama-Bin-Laden)
In IKL, this asserts that Osama-Bin-Laden simply has a property,
without any qualification as to time or circumstances; and with the
usual meaning of Dead, this example IKL sentence is clearly false. The same sentence form asserted in a tense logic, however:
(Dead Osama-Bin-Laden)
is a time-dependent indexical sentence, it will be true or false depending on the time it is understood to be asserted at. Applying the future tense operator to it:
(Future (Dead Osama-Bin-Laden))
produces a time-dependent indexical sentence which is true whenever it is asserted, since the inner sentence will always be true at some future point. Similarly, the same sentence written in the context logic ICL:
(Dead Osama-Bin-Laden)
is understood as a shorthand for the contextual assertion
(ist IdentityContext (Dead Osama-Bin-Laden))
asserted relative to a special 'identity context'. [*18]
This is all in sharp contrast with the central IKL design. When translating content into IKL from such indexical logics, it is important to carefully note the implicit assumptions of the 'plain assertion' case and to transcribe sentences accordingly. It is almost never corrrect to simply transcribe simple sentences from a modal or indexical logic into IKL without transforming them in some way, since their meaning in an indexical framework is almost always different from their meaning in a non-indexical logic. [*19]
We will refer to the the implicit time or index or context,
associated by the logic with the assertion of an unmarked sentence, as
the base context. Each modal or contextual framework needs to
have its particular base context conditions made explicit, because they
influence what the sentences of the framework mean; for example, a
sentence of a tense logic will change its truth-value as the time of
utterance changes. For this reason, modal and context logics have
inherent limitations of expressivity. For example, a context logic such
as ICL cannot directly represent simple non-contextual truths such as (= (plus 2 2) 4), and a modal tense logic cannot express relationships between the same thing at different times (such as Bill is taller than he was.)
This in turn means that it may be impossible to translate all IKL
content back into such a logic: for example, simple equations in IKL
cannot be translated into ICL.
IKL can represent all contextual and modal content in a single
uniform framework, by using a relation between the indexical 'things'
relative to which the sentence's truth is assumed to be asserted – for
example, these might be contexts, times or believers – and
propositions representing the content of the indexical sentence. As this
is very similar to the idea of an assertion relative to a context, it
is natural to use the context-logic relation ist (is true in) to write these atomic sentences. For example
(ist TemporalContextDay06-16-2006 (that (Dead Osama-Bin-Laden)))
is a natural IKL rendering of the ICL sentence (Dead Osama-Bin-Laden) asserted in a context TemporalContextDay06-16-2006. [*20]
This translation style can of course be applied to any sentence, no matter how complex, since any such sentence can be transformed into an IKL proposition name; and the 'inner' names can be quantified in any pattern.
(ist TemporalContextYear1995
(that (exists ((x isHuman)) (and (Democrat x)(PresidentOfUSA x))))
)
The standard translation of modal sentences is similar, but rather than simply relating the proposition to a base context or to a named context, it involves quantifying over contexts which are related to the base context. The particular base and relation are determined by the particular logic and modality.[*21] For example, the future tense of a sentence means that the sentence is true at some time later than the temporal base context time of utterance assumed by all temporal logics. The temporal modal sentence
(Past (exists ((x isHuman)) (and (Democrat x)(PresidentOfUSA x))))
where Past is the simple past tense, translates to
(exists ((t time))(and
(before t now )
(ist t (that (exists ((x isHuman)) (and (Democrat x)(PresidentOfUSA x))))
))
where before is the temporal ordering and now is the temporal base context. [*22]
The simple past and future tenses are examples of 'weak' modalities which map naturally to existential sentences; the dual notion of a 'strong' modality, such as the strong past tense until now or the strong future from now on or henceforth, map into universal quantifiers:
(Henceforth (exists ((x isHuman)) (Alive x)) )
translates to
(forall ((t time))(if
(before now t)
(ist t (that (exists ((x isHuman)) (Alive x)) ))
))
More complex modalities can be mirrored by more complex patterns of quantification. For example, the continuous tenses assert that something is true in a time-interval which is related to 'now'. Thus, the 'continuous present' indicated by the English 'ing' ending, as in It is raining, means that the proposition 'rains' is true throughout some interval containing 'now':
(exists ((I TimeInterval))(and
(in now I)
(ist I (that(Precipitation Rain)))
))
There is an extensive literature on such translations and their properties, which we do not have space to review here.
The IKL translation styles given so far have all been concerned with how to express that the truth of sentences may vary between contexts. Since IKL is transparent and panoptic, these translations implicitly assume that names and quantifiers work in the same way inside a modal or contextual sentence as they do in the rest of the logic: that is, they assume that the context or modal logic is transparent and panoptic in the same way that IKL is. This assumption is often made when dealing with temporal and other 'physical' modalities, but is often explicitly not made when formalisms describe 'psychological' modalities or contexts such as believes or knows, which set out to describe mental states in which names might refer differently than they do 'in fact', or contexts representing sources which use names in ways that we must make hypotheses about, but which may differ from how these names are used in the body of an IKL sentence. To represent cases like this in IKL, we must be explicit about the hypothetical or contextual nature of a name.
For example, consider how to express the hypothesis that the name 'The Prince' detected in some source document, is being used there (but not, of course, in general) to refer to Osama bin Laden. Suppose that the content of this source document is rendered in IKL using this same name, and related to a context C2671-A representing the source:
(ist C2761-A (that (and ... (attended Meeting17 "The Prince") ... )))
How can this hypothesis be expressed? It would not be correct to simply write
(= "The Prince" "Osama bin Laden") ???
since in a panoptic logic this says that the names are identical everywhere, but we want to only speak of uses of the name in this particular context. It is not correct to assert this equation inside the context itself
(ist C2761-A (that (= "The Prince" "Osama bin Laden"))) ???
since this identification is not made explicitly by the source itself. We need a non-contextual way to refer to the meaning of a name in a context. This can be done straightforwardly by extending the notion of indirect names. Recall that the indirect name (tnb 'The Prince') refers to "The Prince"; IKL extends this convention by adding the context name as an extra argument to the 'dereferencing' function, so that
(tnb 'The Prince' C2761-A)
refers to whatever the name "The Prince" refers to in the context C2761-A. Such a term is called an opaque contextual name, or simply a contextual name. [*23]
The use of opaque contextual names allows a transparent logic such as
IKL to compactly and efficiently express hypotheses which are normally
understood to require an opaque logic. For example, our hypothesis about
this name can be expressed by the simple equation
(= (tnb 'The Prince' C2761-A) "Osama bin Laden")
Note, however, that since IKL is transparent, this naming discipline of using the contextual name instead of the corresponding simple name needs to be adopted even when expressing the contextual proposition itself. Our earlier sketch of this context sentence is therefore not correct; it should be:
(ist C2761-A (that (and ... (attended Meeting17 (tnb 'The Prince' C2761-A)) ... )))
where the internal names whose referents are context-sensitive are explicitly contextualized by the same context. Whenever a name is being used in a 'local' way, so that what it refers to depends on its context of use, it should be rendered in IKL as a contextual name.
This discipline sometimes produces longer sentence forms than would
be needed in an opaque logic, since the contextual qualifiers need to
be re-iterated for every occurrence of a name inside a contextual
assertion. However, in the case where we can be confident that a name is
being used in a context with the same meaning that it is has elsewhere
– which is the most common case for most names and most contexts
– it allows a direct rendering, using the simple name: in contrast,
an opaque logic treats the contextualization of a name used inside an ist
as a default which needs to be explicitly over-ridden by axioms
involving quantifiers, to establish a link between uses of the same name
'inside' and 'outside' the context, for example in ICL:
(exists (x)(and (= x "Osama bin Laden")(ist C2761-A (= x "Osama bin Laden") )))
Such 'reference frame axioms' are not necessary in a transparent
panoptic logic like IKL: because every occurrence of a name has the same
referent, one simply uses the same name inside and outside the ist.
Also, the availability of a general construction for indicating the
referent of a name in a context means that links between name references
from multiple different contexts can be asserted and used with general
equational reasoning, which is impossible in an opaque logic. For
example, one might wish to give a context name to a hypothesis about the
referents of names in other contexts:
(ist C27-I-3 (that (= (tnb 'The Prince' C2783-A)(tnb 'The General' C2761-A))) )
which is difficult to express in a context logic.
General statements about references of names in contexts can be made by quantifying over character sequences, using tnb appropriately to refer to their referents. For example, we can define a class of contexts which treat all names transparently:
(forall ((c TransparentContext) (s charseq))(= (tnb s c)(tnb s)) )
This equates each contextual name with the similar indirect name,
which by IKL convention means the same as the simple direct use of the
name. Recall that (tnb 'name'), with no contextual argument, means the same as name.
To sum up this section: IKL is transparent, so all occurrences of
any name — indeed, of any term — refer to the same thing no
matter where they occur, even inside propositions asserted contextually
or with qualifications. There are no contextual uses of a name in IKL. So, in order to adequately transcribe from notations which treat names as varying contextually, all such 'contextually sensitive' occurrences of names must be translated into contextual names, i.e. terms of the form (tnb S C)where
S is a character sequence corresponding to the name in question, and C
is the local context in which the name is being understood. This applies
to all names, even names used to refer to relations and
functions, and names of other contexts; but it is necessary only when
there is reason to suppose that the context does indeed use names in
context-specific ways.
The effect of 'nested' contexts in ICL — that is, the use of a context name inside another contextual assertion which, because of the opacity of ICL, might re-interpret the context name itself — is obtained in IKL by replacing the inner context name by a contextual name using the outer context. For example, the ICL sentence:
(ist Context1 (ist Context2 (simple sentence)))
maps to the IKL
(ist Context1 (that
(ist (tnb 'Context2' Context1) (that
((tnb 'simple' (tnb 'Context2' Context1)) (tnb 'sentence' (tnb 'Context2' Context1)))
))
))
in which the rather complex terms [*24] make explicit the implicit variability of the ICL names when used inside a contextual sentence. In ICL, all names are opaque, since ICL allows all names to be re-interpreted by an 'outer' context. Again, however, we note that this degree of contextual precision is needed only when there is reason to suppose that the inner context name is being used in a contextually sensitive fashion.
istAll of the modal/context translations given so far take a sentence in the original modal or contextual logic into a proposition name in IKL. In many cases, this use of proposition names can be eliminated by further translations which convert
(ist C (that S))
into a modified version of the sentence S in which the context name
has been directly incorporated into the first-order syntax. This allows
the resulting translation to be used by conventional reasoning engines
which do not recognized the ist or that
constructions. This is often done for contexts representing times or
possible states of a world, for which the truths in a context are always
logically consistent: the psychological modalities which are required
to be able to express inconsistent contexts are usually best left
written using ist and proposition names.
This general style of translation has been re-invented many times and is widely used, in various forms, throughout KR and AI planning. As the general technique is well-known, and in many cases this extended translation is not needed for interoperation, we will here only briefly survey the general idea and give the main results and some examples.
The idea is to transform an expression (ist C (that S)),
where S is a sentence, into some combination of similar expressions
made up from the immediate syntactic parts of S, and so 'push ist
inwards' by applying these transformations recursively, until one
reaches atomic sentences, and then to use some systematic way to attach
the context name to the resulting atom. The details of this
transformation vary somewhat depending on the properties of the original
logic, however.
It is generally assumed that ist is transparent to conjunction, i.e. that all contexts are A-clear, where
(forall (c)(iff (A-clear c)
(forall (p ...) (iff
(ist c (AND p ...)))
(and (ist c p)(ist c (AND ...)))
))
))
Although there are natural uses of 'true in a context' which are not A-clear, they can usually be replaced by a suitable quantification over subcontexts which are. For example, the idea of being true at some time during an interval, as in "it rained on Saturday", is not A-clear, but can be treated as a weak modality and hence translated into the form
(exists ((i timeInterval))(and
(subInterval i Saturday)(ist i (that (Precipitation Rain)))
))
where the ist now means true throughout the interval, which is A-clear.
Recent work [Hayes05] has established very general conditions under which any A-clear notion of truth in a context may be thought of as a form of strong modality with the meaning true in all pointlike subcontexts of the context, where a pointlike subcontext is one that has no subcontexts and hence is both A-clear and N-clear, i.e. transparent to both conjunction and negation:
(forall (c)(iff (N-clear c)
(forall (p) (iff
(ist c (that (not (p))))
(not (ist c p))
))
))
The utility of this is that if a context is both A-clear and N-clear then it is transparent to all the Boolean connectives. This also conforms to the usual assumption underlying temporal modal semantics that a 'time' is a single time-point.
This second reduction to AN-clear contexts can always be done
provided that contexts have a well-defined notion of 'subcontext' and
are such that it is impossible for a logical contradiction to be true in
a context.[*25] Both
of these conditions are true for any notion of context corresponding to a
piece of a possible world or set of actual circumstances, such as a
time-interval or a geographical region; what Menzel [Menzel99]
calls an "objective" context. They may not hold for some kinds of
psychological context, as for example if one wishes to describe the
mental state of a believer who has contradictory beliefs by asserting
that the contradiction is "true in a belief context". In this kind of a
case, it may be difficult or impossible to completely eliminate the ist construction, although in many cases it can be greatly restricted, as Makarios shows [Makarios06].
Such attributions of contradictory beliefs are however problematic for
any logical reasoner; it is not clear what it means to say that
contradiction is true, even "in" a context.
If c is both A-clear and N-clear, then we can 'push ist inside' any Boolean sentence form, by replacing all the connectives by their conventional reductions to and and not. For example, (if(p)(q)) is equivalent to (not(and(p)(not(q))), so the following are equivalent:
(ist c (that (if (A) (B))))
(ist c (that (not (and (A) (not (B))))))
(not (ist c (that (and (A)(not (B))))))
(not (and (ist c (that (A)))(ist c (that (not (B)))) ))
(not (and (ist c (that (A))(not (ist c (that (B)))) ))
(if (ist c (that (A)))(ist c (that (B))))
Clearly the same kind of process works for any Boolean combination.
It remains only to consider the case where P is a proposition expressing a quantified sentence. Since the existential quantifier is the negation dual of the universal, we need only consider one of them in detail.
(ist C (that (forall (x)( ... )))
Here there are two cases, depending on how the original logic
treats quantifiers in a context. Some context logics (CycL and ICL are
examples) treat quantifiers similarly to a panoptic logic, so that all
quantifiers range over the same 'global' universe, no matter in what
context the quantifier occurs. In this case, the quantifiers are of
course transparent to ist:
(forall (c p)(iff
(ist c (that (forall (x)(p))))
(forall (x)(ist c (that (p))))
))
and similarly for exists, and we have a complete reduction to the atomic case, since any IKL sentence can be rewritten in an equivalent form just using and, not and forall. Some indexical logics, however, treat the quantifiers as ranging over individuals which exist in the particular context,
and not over individuals which exist in other contexts. For example,
some temporal logics treat the universal quantifier as meaning 'for all
things existing at the current time'. A logic which uses this style of
'contextual quantification' requires a more complex translation, because
we must restrict the quantifier when it is taken outside the scope of
the ist. We will use a function existsIn from contexts to predicates on individuals to state this: ((existsIn C) x) is true when x is an item in the universe of quantification of the context C; and then the translation involved in pushing ist inwards past the universal quantifier is expressed by the following axiom:
(forall (c p)(iff
(ist c (that (forall (x)(p))))
(forall ((x (existsIn c))(ist c (that (p))))
))
When using this kind of translation it is important to ensure that the existsIn
is applied to the contexts at the correct granularity. For example, if
truth in a context is rendered as truth at all point-like subcontexts of
the context (to ensure N-transparency, as described earlier) then existsIn
should be applied to the points, not to the larger intervals, since a
thing might exist during only part of a longer interval. This becomes
important when translating sentences which refer to contexts whose
extent is greater than the lifespan of the individuals over which one is
quantifying, for example "In nineteenth-century Europe, many people died of cholera." Again, there is a considerable literature on these issues, which we do not have space to survey completely. [*26]
Using the various techniques just given, one can usually reduce (ist C (that P)) to some more or less complicated expression in which the only occurrences of ist are where P is an atomic sentence. A notational convention then finally eliminates the ist
by inserting the context name into the atomic sentence in some way.
Several such devices have been used in the KR literature, in some cases
from the very beginning of the subject. The classical technique is to
simply insert the context as an extra argument, usually the last, to the
relational operator of the atomic sentence, for example:
(ist c (that (Married "Muhammed bin Laden" "Hamida al-Attas")))
==>
(Married "Muhammed bin Laden" "Hamida al-Attas" c)
Relations which takes a temporal context as a parameter in this way can be thought of as 'changing relations', and are often called fluents, and the temporal parameter called a situation; the technique and both terms were introduced by John McCarthy [McCarthy 63] and the resulting theory was christened 'situation calculus' and shown equivalent to a first-order translation of a modal temporal language in [McCarthyHayes 69].
However, other ways of embedding the context are possible. It may be added as an argument to every name in the atom, in effect treating them as contextual functions:
(Married ("Muhammed bin Laden" c) ("Hamida al-Attas" c))
This technique was used in [Hayes 79] where the entities being 'time-sliced' were called histories and thought of as pieces of a 4-dimensional continuum, although that metaphysical perspective is not required in order to use the formal technique.
Another technique is to re-cast the relation of the atom as a function to a predicate on contexts, so that the original atom becomes a complex relational term:
((Married "Muhammed bin Laden" "Hamida al-Attas") c)
This is used by PSL [PSL], for example. Other variations are possible.
Although these are all merely syntactic variants, they each suggest different styles of conceptualizing the world, and therefore come with philosophical baggage. Probably because of this, they have all been discussed, defended and criticised extensively in the AI/KR literature. For interoperability purposes, however, these philosophical debates are largely irrelevant. All that really matters is that some consistent policy is adopted for attaching contexts to atomic sentences, as it is a straighforward matter to write conversion axioms in IKL which will render the various styles equivalent. For example:
(forall (r (c context) ...)(iff (r ... c)((r ... ) c) ))
will make the 'situation calculus' and 'PSL' styles equivalent, so that they may be used freely together. [*27]
[*1] Not a standard logical term.
[*2] The bare quantifier 'exists' in IKL therefore should not be read as meaning 'exists in the real world' or 'is actual', but something more like 'can be possibly referred to'.
Any name which can be used by anyone to refer to anything, real or
imaginary, or any thing which anyone considers to 'exist' in any sense,
or which has existed in the past or will exist in the future, or even is
simply something whose existence is being considered hypothetically;
these all count as things which exist in the IKL universe. It is all-inclusive.
[*3] This usually requires a fairly elaborate set of declaration conventions to declare sorts, assign sorts to identifiers (that '17' has the sort number and 'PatHayes' has the sort human) and to argument places of relations and functions (that plus has the sort [Integer x Integer -> Integer])
so sorted languages typically have an associated sub-notation concerned
with making such sort declarations. Other sorted languages assume a
fixed set of sorts, built into the language: many higher-order logics
have this character, where the sorts are referred to as (higher) types, and the resulting notation called type theory.
[*4] Note a
possible source of misunderstanding. Many of these can be naturally read
as though they were written as infixes, so that for example (and A B C) can be read as A and B and C. However, this heuristic reading is misleading for implication, since (if A B) means if A then B, but when naively rendered as an infix, it means the opposite: A if B is usually read as A, if B, which is the natural rendering of if B then A. One way to guard against this is to think of the implication syntax as an abbreviation for if...then: (if A [then] B), with the 'then' omitted. Another way is to remember that the direction of the implication is always from left to right, so that (if A B)
means that one can correctly infer from A to B. The old KIF symbol '
=>' makes this vividly clear, but this symbol was abandoned in Common
Logic because in XML-compliant text it has to be written as =>
[*5] KIF for example assumes that any name begining with a query mark is a variable, and that any free variable is universally quantified at the top syntactic level. Since IKL has no syntactically distinguishable category of variable, it has no such convention, and all quantifiers must therefore be indicated explicitly.
[*6] Common Logic has been characterized as "higher-order syntax with a first-order semantics"; but see footnote *9 for an important qualification.
[*7] Zero is excluded because (exists 0 (y) ... amounts to (not (exists (y)... .
[*8] It would not have a well-defined meaning in any case: are there three <x,y> pairs, or nine?
[*9] The quantifier (forall (r...
in this example above can be read intuitively as saying 'for all
relations'; but 'all' here means only 'all relations which are in the
universe', which can be a much smaller set than all mathematically
definable relations. Unlike higher-order logics, IKL does not have any
comprehension principles built into it which would guarantee the
existence of functions or relations (other than propositions): this is
what keeps IKL a genuine first-order language. In general, such
'higher-order' quantifications in IKL should be understood as applying
only to functions or relations which are indicated by expressions which
can be built from the axioms themselves. For normal purposes of
expressing real-world knowledge, this is not a real limitation; it
becomes an issue only when using the logic to express theorems in higher
mathematics.
[*10] Note the difference between '...' which is part of the IKL syntax, and the simple ellipsis '...' which used in the text in the usual way.
[*11] The OR defined here can be thought of as an operation on classes, and it then corresponds exactly to the OWL [OWL] operator owl:unionOf. Later sections describe in detail how to transcribe description logics such as OWL into this style of IKL usage.
[*12] Many languages use the prefix /u for Unicode escaping.
[*13] This differs sharply from the XML convention whereby single and double quotes are interchangeable.
[*14] The backslash-escaping might make these look different when the enclosed name or quoted string contain their own quotation marks:
(= "Christopher (\"Chris\") Menzel" ('Christopher ("Chris") Menzel') )
(= "Michael ('Mike') Gruninger" ('Michael (\'Mike\') Gruninger') )
and the Unicode hexadecimal escaping convention allows the same character sequence to be written using different lexical conventions:
(= '\0077\0068\006F\006F\0070\0073' 'whoops')
but with these exceptions, the name and the quoted string will differ only in their outer quote marks.
[*15] This is the classical distinction between de re and de dicto belief attributions.
[*16] This section is not a full account of how to exactly capture the OWL-DL specifications, which are quite complex and require a great deal of attention to such details as distinguishing between datatype values and other entities. A more exact translation of semantic web languages into CL is given in [SW2CL].
[*17] Although IKL does not require any distinction to be made between individuals, unary and binary relations, description logics usually do, so we are here maintaining the required discipline. However, other uses of these names – for example, using a 'class' name as, say, a binary relation – are harmless in IKL, and will not impair these defined terms or create any kind of IKL error or logical contradiction.
[*18] In a true context logic, all assertions are made 'in' a context, even the basic axioms of a theory, so a simple non-contextual assertion is, strictly speaking, impossible.
[*19] Some contextual frameworks, such as that used by Cyc, have a 'universal' context which is intended to be the index for assertions which are 'simply true', and from which all other contexts inherit any assertions. In many respects such a framework is similar to a panoptic logic such as IKL.
[*20]A more realistic way to render such an example would be to use a term built using the XSD datatype conventions to denote the temporal context:
(ist (TemporalContext (xsd:dateTime '2002-10-10-T12:00:00-05:00'))
(that (Dead Osama-Bin-Laden))
)
Note how this differs from the standard ICL 'base case' of this simple sentence, which would be
(ist IdentityContext (that (Dead Osama-Bin-Laden)))
which is almost a direct transcription of the ICL form, but from which nothing follows about the truth or falsity of the sentence in any other context.
[*21] This style of translation is a standard way to map modal langauges into a non-modal framework; it faithfully captures the 'standard' Kripkean modal semantics (see [Kripke]).
[*22] In a truly adequate IKL translation, [now] should be replaced by a reference to an actual time-point, for example by a term of the form (xsd:dateTime '2002-10-10-T12:00:00-05:00'), denoting the 'utterance context' in which the indexical modal assertion was understood to be made.
[*23] The expression can be shortened somewhat, at a possible cost in readability, by simply omitting the 'tnb',
which is an optional 'dummy' relation, and using the character
sequences directly as function names. The example in the text then looks
like this:
(ist Context1 (that
(ist ('Context2' Context1) (that
(('simple' ('Context2' Context1)) ('sentence' ('Context2' Context1)))
))
))
[*24] One way to
think of a contextual name is as a subscripted version of the name,
where the context names serves as a subscript. But it is important to
bear in mind that there is no logical relation between the plain
name and its subscripted version; they are simply two different names
which are lexically similar, like 'Patrick' and 'trick'.
[*25] There are some more abstruse mathematical conditions, but they are satisfied by all reasonable notions of 'context'.
[*26] Some of the intricacy involved can be illustrated by the following example. Imagine a conveyor belt taking crushed coal from a crusher to a furnace, and suppose that the lifetime of a typical piece of coal on this conveyor, between the time it is created by the crusher to the time it is consumed by the furnace, is a minute. To say that the conveyor is operating correctly for an hour in a non-panoptic temporal logic, one might assert
(ist HourContext (that (exists ((x coalpiece)(on x conveyor))))
Moving ist inwards on this formula correctly will produce something like this:
(forall ((I timeInterval)(if
(subinterval I HourContext)
(exists ((J timeInterval) (x coalpiece))
(and (subInterval J I)(existsDuring x J)
(forall ((t timePoint))(if (in t J)(ist t (that (on x conveyor)))))
))
))
and all of these quantifiers are necessary to correctly capture the precise meaning of the original. The distinction between I and J is necessary to cover the case that x's lifetime overlaps I but neither contains the other.
[*27] For a more
nuanced and careful translation, it would be wiser to distinguish the
various uses as frameworks and then to write axioms which translate
between them explicitly, for example by using the frameworkName and tnb functions:
(forall ((s charseq)(c context) ...) (iff
((tnb (frameworkName SitCalc s)) ... c)
(((tnb (frameworkName PSL s)) ... ) c)
))
The IKL semantics guarantees that to all IKL sentences there is a
corresponding proposition which is true when the sentence is true, and
all such propositions are first-class 'things' in the universe of
discourse, so can be referred to by other names and quantified over.
However, it does not specify exactly when two sentences define the same
proposition. The minimal condition on propositional identity are that a
change of bound names in a sentence does not change the proposition
expressed by the sentence, so that for example (that (exists (x)(loves Jim x))) equals (that (exists (y)(loves Jim y))).
Moreover, the proposition depends on the things named in the sentence,
not on the names used to refer to them, so using a different name to
refer to the same thing does not change the proposition. Apart from
these conditions, however (which can be summed up by saying that a
proposition expressed by a sentence is about the things named by the free names in a sentence), no stronger conditions are imposed by the IKL semantic construction.
One might argue that logically equivalent sentences should always
express the same propositions, but this would make the problem of
determining propositional identity computationally hard or even
undecideable; or, on the other hand, that only 'obviously' equivalent
sentences should (e.g. (that (and (p)(q))) vs. (that (and (q)(p)))),
but it is tricky to come to universal agreement on what counts as
'obvious'. The Interoperability WG therefore has decided to not impose
any such 'obviousness' conditions on IKL propositions, but to allow
propositional identity to be defined by axioms, and to include in IKL a
predefined relation of propositional equivalence, written =p,
embodying what the IKRIS interoperability working group considers to be
the most universally appropriate such conventions, and intended to be
used as a 'practical' propositional identity relation, intuitively
meaning 'saying the same thing'. Users who prefer to use a different notion may define and use other notions of propositional equivalence.
IKL propositional equivalence is reflexive, transitive and symmetric and satisfies the following identities, for any sentences PHI , RHO, KAP, etc.:
(=p (that (and )) (that (and RHO PHI)) )PHI RHO KAP ...
(=p (that (or ))(that (not (and (not PHI)(not RHO)(not KAP)...))))PHI
(=p (that (and (and RHO KAP)))(that (and (and (PHI RHO) KAP))))PHI RHO
(=p (that (if )(that (or (not PHI) RHO)) )PHI RHO
(=p (that (iff ))(that (and (if PHI RHO)(if RHO PHI))))PHI PHI
(=p (that (and ) (that PHI))
In addition, propositional equivalence satisfies quantifier duality for any name n and any sentence PHI,
(=p (that (forall (n) PHI)) (not (exists (n) (not PHI ))) )
In addition, as stated above, the IKL semantics ensures that for any names n and m, and any sentence PHI containing a free occurrence of n which does not occur in the scope of any quantifier which binds m,
(=p (that (forall (n) PHI)) (that (forall (m) PHI[n/m] )) )
must be true, where PHI[n/m] is the sentence obtained by substituting m for every free occurrence of n in PHI,
when the substituted name is also free. That is, expressed less
formally, changing the bound variable name in a quantifier does not get
you a different proposition. =p is then defined as the
smallest relation satisfying all these conditions, i.e. the relation
which these conditions recursively define.
This definition of propositional equivalence is work by John Sowa who has shown that =p
can be decided by transforming all sentences to a normal form and then
comparing the resulting character strings, using a transformation that
is at worst n.log(n) in the length of the sentence: it reduces sentences to the vocabulary (exists, not , and), removes duplications and puts atomic sentences and bound variables into an arbitrary but fixed lexical order (see [SOWA] , where =p is called 'f4' ).
One important property is that equivalent propositions are always about the same things, i.e. if two sentences express equivalent propositions, then the set of things referred to by the names which occur free in the sentences are the same.
It is easy to write IKL sentences which seem to describe impossible propositions, for example
(= p (that (not (p))))
or equivalently
(= p (that (not (isTrue p))))
which is a succinct rendering of the classical liar paradox, being
apparently a description of a proposition which asserts its own falsity.
In IKL this is not paradoxical, but it is inconsistent. Thus the above
equation, which has the form of a simple definition of the name p, is in fact a contradiction, like
(and (p)(not (p)))
It is characteristic of IKL that paradoxes translate into IKL
"definitions" which are inconsistent. This fact, that sentences which
appear to be definitions can be inconsistent, is the price IKL pays for
being able to talk freely about the propositions that its own sentences
assert. In this case, for example, there simply is no such proposition p satisfying this equation, which accounts for its inconsistency. Put another way, the following is a logical theorem in IKL:
(forall(p)(not (= p (that (not (p)))))
Other examples of apparent paradoxes which can be written as inconsistent sentences in IKL include the Russell paradox:
(forall (x)(iff (Russell x)(not (x x))))
which has the form of the definition of a property Russell,
which in this case is the "impossible" property which, if it existed,
would be true of exactly the things that are not true of themselves, and
so be true of itself exactly when it isn't. Since no such Russell can possibly exist, this "definition" of it is, again, inconsistent; the following is an IKL logical truth:
(forall (R)(not ((forall (x)(iff (R x)(not (x x))))))
More recently, Kripke [Kripke75] has identified a family of 'contingent paradoxes', which Christopher Menzel (personal communication) has shown can also be written in IKL. The simplest is:
(forall (x)(iff (IsFalse x)(= x (that (forall (q)(if (IsFalse q)(not (q))))))))
Here, the IsFalse is the "impossible" property of
being exactly the proposition that all propositions which have this
property are false. Note that as in the Liar, this inconsistent
definition uses the defined name in the "defining" expression.
In this last case it is not completely clear whether it is the
property itself, or the proposition which it is true of, which is
'impossible', and indeed a formal semantics for IKL could be constructed
based on either intuition. The IKL semantics chooses the former, which
has the effect of retaining the general principle that (isTrue (that SENT)) is always equivalent to SENT,
but at the cost of allowing inconsistencies, like the above sentences,
which appear to have the innocuous form of a property definition.
Choosing the other alternative would mean that not all proposition names could be interpreted as denoting coherent propositions, so that the above equivalency principle would have to be restricted to some class of 'properly formed' sentences (which would exclude, for example, the forms used in the above examples.) This alternative design is safer but requires users to avoid 'ill-formed' proposition names. As this is restriction is a potential burden on users, we have chosen ease of professional use over safety. In practice, this means that it is the user's responsibility to avoid such 'paradoxical' contradictions. They are however most unlikely to arise in practice, as they need to be carefully constructed. As a guideline, it is usually a safe strategy to avoid making assertions which relate a name to any proposition-forming term which uses that very name itself, particularly in a negative context (negated, or stated to be equal or equivalent to a negated self-applicative form.) It is exactly such 'self-referential loops with negation' which tend to produce these inconsistencies. It is not sufficient to simply avoid the particular cases listed above, however, since this kind of impossible situation can be reconstructed at an arbitrary depth of syntactic complexity, e.g. by writing a "definition" of the the impossible binary relation between propositions which holds just when one of them is the proposition that nothing stands in this relation to another proposition, etc..
Finally, notice that not all circular definitions need be contradictory. For example, the 'Truth-Teller' sentence says of itself that it is true, so can be consistently asserted or denied. The IKL version of this
(= p (that (p)))
fails to define anything simply by virtue of being vacuous: it is consistent with either (p) or (not(p)); but not, of course, with both.
Bill Andersen
Richard Fikes
Patrick Hayes
Charles Klein
Deborah McGuinness
Christopher Menzel
John Sowa
Christopher Welty
Wlodek Zadrozny
[CL] Common Logic - A framework for a family of Logic-Based Languages, ed. Harry Delugach. ISO/IEC JTC 1/SC 32N1377, International Standards Organization Final Committee Draft, 2005-12-13 http://cl.tamu.edu/docs/cl/32N1377T-FCD24707.pdf
[Hayes79] Patrick J. Hayes, "The Naive Physics Manifesto." In Expert Systems in the Microelectronic Age, D. Michie (ed.), Edinburgh University Press, 1979.
[Hayes05] Patrick J. Hayes, Context Mereology, Unpublished IKRIS memorandum, 2005. http://www.ihmc.us/users/phayes/context/ContextMereology.html
[IKLSPEC] Patrick J. Hayes & Christopher Menzel, IKL Specification Document. Unpublished IKRIS memorandum, 2006. http://www.ihmc.us/users/phayes/IKL/SPEC/SPEC.html
[KIF] Knowledge Interchange Format, Michael R. Genesereth et. al., 1998 (draft American National Standard).
[Kripke63] Saul Kripke, "Semantical Considerations in Modal Logic", Acta Philosophica Fennica 16:83–94, 1963 (See: Kripke semantics, Wikipedia article. http://en.wikipedia.org/wiki/Relational_semantics)
[Kripke75] Saul Kripke, "Outline of a Theory of Truth", Journal of Philosophy 72: 690-715, 1975
[Makarios06] Selene Makarios, Karl Heuer and Richard Fikes, "Computational Context Logic and species of $ist$", Unpublished memorandum, Stanford Knowledge Systems Laboratory KSL-06-07, 2006. http://ksl.stanford.edu/KSL_Abstracts/KSL-06-07.html
[McCarthy63] John McCarthy. Situations and Actions and Causal Laws. Stanford Artificial Intelligence Project, Memo 2, 1963.
[McCarthyHayes69] John McCarthy and Patrick J. Hayes, "Some Philosophical Problems from the Standpoint of Artificial Intelligence", In Machine Intelligence 4, editors B. Meltzer and D. Michie, pp. 463--502, Edinburgh University Press, 1969. http://www-formal.stanford.edu/jmc/mcchay69/mcchay69.html
[Menzel99] Christopher Menzel, "The Objective Conception of Context and Its Logic", Minds and Machines, 9, (1999) 29-56. http://philebus.tamu.edu/~cmenzel/Papers/mm-paper.pdf
[OWL] OWL Web Ontology Language Overview, eds. Deborah L McGuinness & Frank van Harmelen, W3C Recommendation 10 February 2004. http://www.w3.org/TR/owl-features/
[PSL] Schlenoff, C., Gruninger M., Tissot, F., Valois, J., Lubell, J., Lee, J., "The Process Specification Language (PSL): Overview and Version 1.0 Specification," NISTIR 6459, National Institute of Standards and Technology, Gaithersburg, MD., 2000. http://www.mel.nist.gov/psl/
[RDF] Resource Description Framework (RDF): Concepts and Abstract Syntax, Graham Klyne and Jeremy J. Carroll, Editors, W3C Recommendation, 10 February 2004, http://www.w3.org/TR/rdf-concepts/ .
[SOWA] John F. Sowa, Propositions. Unpublished memorandum. <http://www.jfsowa.com/logic/proposit.htm>
[SW2CL] Patrick J. Hayes, Translating Semantic Web Languages into Common Logic, Unpublished memorandum, 2005. http://www.ihmc.us/users/phayes/CL/SW2SCL.html
[XSD] XML Schema Part 2: Datatypes, Biron, P. V., Malhotra, A. (Editors) World Wide Web Consortium Recommendation, 2 May 2001 http://www.w3.org/TR/xmlschema-2/