Analogical Reasoning


John F. Sowa   and   Arun K. Majumdar

VivoMind LLC




International Conference on Conceptual Structures (ICCS)

25 July 2003










 

Methods of Reasoning

Peirce's classification:

  1. Deduction:  Deriving implications from premises.

  2. Induction:  Deriving general principles from examples.

  3. Abduction:  Forming a hypothesis which must be tested by induction and deduction.

  4. Analogy:  "Besides these three types of reasoning there is a fourth, analogy, which combines the characters of the three, yet cannot be adequately represented as composite." (Peirce, ms L75, 1902)








 

Peirce's Logic of Pragmatism









 

Sensory-Reasoning-Motor Cycle

  1. Induction:  From observations to generalizations to the "knowledge soup."

  2. Abduction:  Extract hypotheses from the soup to form a tentative theory.

  3. Revision:  More abductions to revise the theory.

  4. Deduction:  Use the theory to make predictions.

  5. Action:  Test predictions by changing the world.

  6. Repeat from line #1.








 

Deductive Systems

  • Better at deduction than most human beings.

  • But they require people like Sherlock Holmes to represent knowledge.

  • At a cost of $10,000 to encode one page from a textbook.








 

Induction and Abduction

  • Computer systems are very good at deduction.

  • They can process large volumes of data for induction and abduction.

  • But they cannot compete with a child in learning language.

  • Why not?








 

Simulating Sherlock Holmes









 

Ibn Taymiyya Contra Aristotle

  • Fourteenth-century Islamic legal scholar.

  • Admitted that deduction is necessary for pure mathematics.

  • But for reasoning about the world, deduction is limited to the accuracy of the induction.

  • Given the same data, analogy can replace induction + deduction.








 

Ibn Taymiyya's Argument

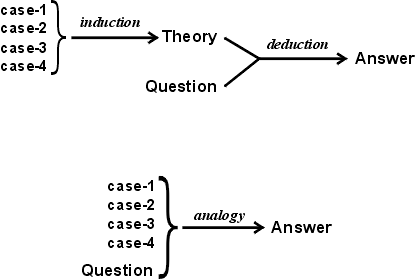
  • A theory can be useful, if available.

  • But analogy can be used when no theory exists.








 

Structure Mapping

Mapping one conceptual structure to another can have four logical effects:

  1. Equivalence:  CS1 ≡ CS2

  2. Generalization:  CS1 ⊃ CS2

  3. Specialization:  CS2 ⊃ CS1

  4. Similarity:  Neither one implies the other.

Analogy uses all four.

Logic uses only the first three.







 

VivoMind Analogy Engine

Structure-mapping methods used in analogy:

  1. Matching labels: 

    • Compare type labels on conceptual graphs.

  2. Matching subgraphs: 

    • Compare subgraphs independent of labels.

  3. Matching transformations: 

    • Transform subgraphs.

Methods #1 and #2 take (N log N) time.

Method #3 takes polynomial time (analogies of analogies).







 

Weight of Evidence

Evaluate analogies based on closeness of match:

  1. Matching labels:  Distance in type hierarchy.

    • Identical:  Cat to Cat.
    • Subtype & supertype:  Cat to Animal.
    • Siblings of common supertype:  Cat to Dog.
    • Distant cousins:  Cat to Tree.

  2. Matching subgraphs:  Based on size.

    • Isomorphic graphs.
    • Large isomorphic subgraphs.
    • Graphs become isomorphic after adjustments.

  3. Matching transformations:  Based on frequency.

    • How often are the transformations used?
    • How complete is the coverage?




 

Analogy of Cat to Car

CatCar
headhood
eyeheadlight
corneaglass plate
mouthfuel cap
stomachfuel tank
bowelcombustion chamber
anusexhaust pipe
skeletonchassis
heartengine
pawwheel
furpaint

VAE uses methods #1 and #2.

Source data from WordNet mapped to CGs.





 

Matching Labels

Corresponding concepts have similar functions:

  • Fur and paint are outer coverings.

  • Heart and engine are internal parts with a regular beat.

  • Skeleton and chassis are structures for attaching parts.

  • Paw and wheel support the body, and there are four of each.








 

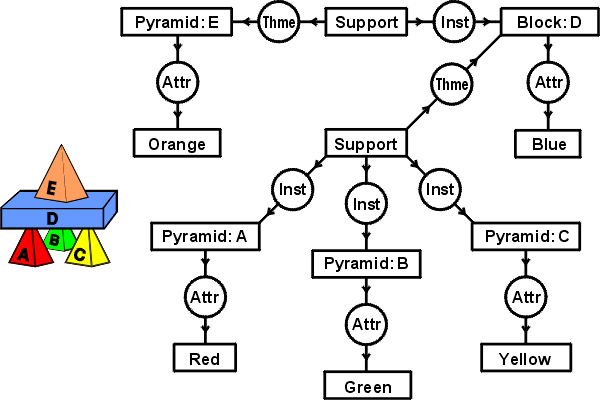
Matching Subgraphs

A pair of isomorphic subgraphs:

  • Cat:  head → eyes → cornea.

  • Car:  hood → headlights → glass plate.

Approximate match (missing esophagus and muffler):

  • Cat:  mouth → stomach → bowel → anus.

  • Car:  fuel cap → fuel tank → combustion chamber → exhaust pipe.






 

Finding Transformations

Method #3 relates different conceptual structures that represent "the same thing."

 
CG derived from English sentence   CG derived from relational database

How can one representation be transformed to the other?











 

Transformations Found by VAE


Top transformation applied to 5 subgraphs.

Bottom one applied to 4 subgraphs.

One application could be due to chance, but 4 or 5 contribute strong evidence for the mapping.

See the paper for details.







 

A Generalization Hierarchy









 

Canonical Formation Rules

Six rules for mapping one CG to another.

  • Equivalence rules:  Copy, Simplify.

  • Specialization rules:  Restrict, Join.

  • Generalization rules:  Unrestrict, Detach.

Any CG can be converted to any other CG by some sequence of these rules.

Similar rules can be defined for any version of logic.







 

Copy and Simplify












 

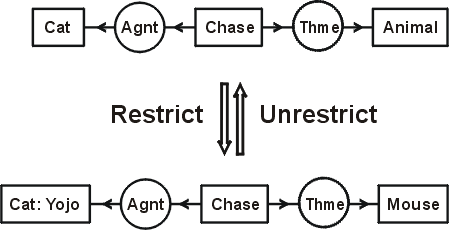
Restrict and Unrestrict












 

Join and Detach












 

Effect of Negation

  • Equivalence rules:  Unaffected by negation.

  • Generalization rules:  Become specialization rules.

  • Specialization rules:  Become generalization rules.

  • Double negation:  Drawing or erasing a double negation around any CG is an equivalence rule.











 

Rules of Inference

Generalized version of Peirce's rules:

  • Erasure:  In a positive context, any CG may be generalized.

  • Insertion:  In a negative context, any CG may be specialized.

  • Iteration:  A copy of any CG (or sub-CG) may be inserted in the same context or any nested context.

  • Deiteration:  Any CG (or sub-CG) that could have been derived by iteration may be erased.

  • Equivalence:  Any equivalence rule may be performed in any context.
With minor modifications, these rules can be adapted to any notation for FOL — even natural languages.







 

Conclusions

  • Basic structure-mapping operations are used in logic and analogy.

  • Peirce's rules of inference use the same operations.

  • Similar operations could be adapted to reasoning in natural languages.

  • They can be implemented efficiently in computer systems.

  • They are good candidates for primitive reasoning operations in the brain.








 

References

Paper on analogical reasoning by Sowa and Majumdar:

http://www.jfsowa.com/pubs/analog.htm

Peirce's tutorial on existential graphs, with commentary by Sowa:

http://www.jfsowa.com/peirce/ms514.htm

Selected papers by Peirce on semeiotic and related topics; see his 1903 lectures on pragmatism in vol. 2 for material related to this talk:

Peirce, Charles Sanders (EP) The Essential Peirce, ed. by N. Houser, C. Kloesel, and members of the Peirce Edition Project, 2 vols., Indiana University Press, Bloomington, 1991-1998.

Copyright ©2003, John F. Sowa